Aller au contenu

TP - Parcours de graphe☘

Dans le dossier [NSI], commencez par créer le dossier [E04-Algo_Graphes].

Téléchargez le module TAD_Graphes.py qui contient une implémentation orientée objet de graphe non pondéré et placez ce module dans le répertoire précédent.

Voici l'interface de ce module :

Méthode/Opérations Description
G = Graphe(dico) Initialisation d'un graphe sous la forme d'un dictionnaire dont
  • les clefs sont les sommets du graphe ;
  • les valeurs sont un tableau des voisins (des successeurs) du sommet
Le paramètre dico est initialisé à None par défaut;
G.est_vide() Renvoie True si le graphe est vide, False sinon.
G.sommets() Renvoie le tableau des sommets, sous la forme d'une liste Python.
G.est_oriente() Renvoie True si le graphe est orienté, False sinon.
G.aretes() Renvoie le tableau des arêtes (des arcs si le graphe est orienté), sous la forme d'une liste Python de couples de sommets.
G.voisins(S) Renvoie le tableau des voisins (des successeurs si le graphe est orienté) du sommet S passé en paramètre.
Affichage

Pour visualiser ce graphe, la fonction print() réalise un affichage compatible avec l'application en ligne GraphViz.

Pile et File

Pour implémenter les parcours de graphe, vous aurez besoin d'utiliser des piles et/ou des files. Vous avez le choix :

  • Soit vous utilisez une liste Python en tant que pile ou file.
    Dans ce cas, attention de bien identifier le sommet de la pile ainsi que la tête et la queue de la file.

  • Soit vous utilisez une des structures de données implémentée au début de l'année. Pour cela, téléchargez la structure de pile et la structure de file.
    Ces deux structures sont munies d'une méthode .contient() qui renvoie True si la valeur passée en paramètre est contenue dans la pile ou la file.

Ce TP a pour but de vous faire programmer les algorithmes de parcours de graphe (ainsi que leurs applications) étudiés en cours.
Pour faciliter ce travail, il est conseillé d'utiliser et compléter le fichier « à trous » : TPE04.10.py.

Partie A - Préparer les graphes de test☘

Afin de tester chacune des fonctions à programmer dans ce TP et vous familiariser avec l'interface, programmez les deux graphes ci-dessous dans le « main » de votre programme.

Conseils

  1. Dans le dictionnaire, placez les voisins (les successeurs) par ordre alphabétique.
  2. Affichez chaque graphe avec GraphViz afin de vérifier votre travail au cours de ce TP.

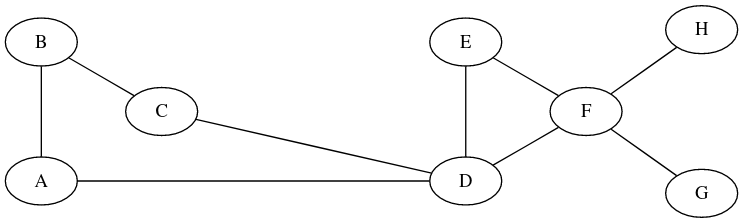
  1. Graphe G1 Premier graphe

  2. Graphe G2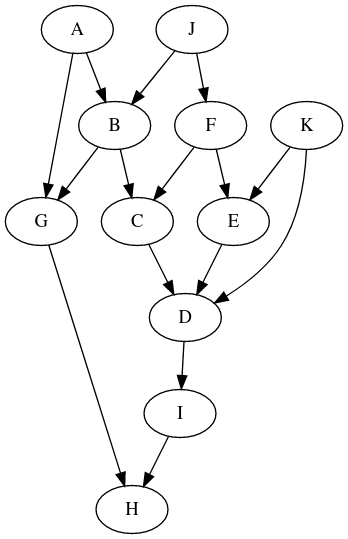 Second graphe

Partie B - Parcours en largeur☘

Complétez la définition de la fonction parcours_largeur() qui prend en paramètres un graphe et un sommet de ce graphe. Cette fonction renvoie un tableau contenant les sommets du graphe visités suite à ce parcours en largeur.

1
2
3
4
5
6
7
def parcours_largeur(graphe, sommet):
    """
    graphe - Graphe, graphe orienté ou non orienté
    sommet - Un sommet du graphe
    Sortie: list, Tableau des sommets du graphe dans l'ordre de leur visite
            par un parcours en largeur réalisé à partir de sommet
    """

Plan de test

Respectez les assertions !

>>> parcours_largeur(G1, 'A')
['A', 'B', 'D', 'C', 'E', 'F', 'G', 'H']

>>> parcours_largeur(G1, 'D')
['D', 'A', 'C', 'E', 'F', 'B', 'G', 'H']

>>> parcours_largeur(G1, 'K')
AssertionError: Le sommet K ne fait pas partie du graphe

>>> parcours_largeur(G2, 'A')
['A', 'B', 'G', 'C', 'H', 'D', 'I']

>>> parcours_largeur(G2, 'D')
['D', 'I', 'H']

Partie C - Parcours en profondeur☘

  1. Complétez la définition itérative de la fonction parcours_profondeur_iter() prend en paramètres un graphe et un sommet de ce graphe. Cette fonction renvoie un tableau contenant les sommets du graphe visités suite à ce parcours en profondeur itératif.

    1
2
3
4
5
6
7
    def parcours_profondeur_iter(graphe, sommet):
    """
    graphe - Graphe, graphe orienté ou non orienté
    sommet - Un sommet du graphe
    Sortie: list, Tableau des sommets du graphe dans l'ordre de leur visite
            par un parcours en profondeur itératif réalisé à partir de sommet
    """

    Plan de test

    Respectez les assertions !

    >>> parcours_profondeur_iter(G1, 'A')
['A', 'D', 'F', 'H', 'G', 'E', 'C', 'B']

>>> parcours_profondeur_iter(G1, 'D')
['D', 'F', 'H', 'G', 'E', 'C', 'B', 'A']

>>> parcours_profondeur_iter(G1, 'K')
AssertionError: Le sommet K ne fait pas partie du graphe

>>> parcours_profondeur_iter(G2, 'A')
['A', 'G', 'H', 'B', 'C', 'D', 'I']

>>> parcours_profondeur_iter(G2, 'D')
['D', 'I', 'H']

  2. Complétez la définition récursive de la fonction parcours_profondeur_rec() qui prend en paramètres un graphe, un sommet de ce graphe et une variable tab initialisée à None. Cette fonction renvoie le tableau tab contenant les sommets du graphe visités suite à ce parcours en profondeur récursif.

    1
2
3
4
5
6
7
8
    def parcours_profondeur_rec(graphe, sommet, tab=None):
    """
    graphe - Graphe, graphe orienté ou non orienté
    sommet - Un sommet du graphe
    tab - list, Tableau des sommets du graphe dans l'ordre de leur visite
            par un parcours en profondeur récursif réalisé à partir de sommet
    Sortie: list, le tableau tab
    """

    Plan de test

    Respectez les assertions !

    >>> parcours_profondeur_rec(G1, 'A')
['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H']

>>> parcours_profondeur_rec(G1, 'D')
['D', 'A', 'B', 'C', 'E', 'F', 'G', 'H']

>>> parcours_profondeur_rec(G1, 'K')
AssertionError: Le sommet K ne fait pas partie du graphe

>>> parcours_profondeur_rec(G2, 'A')
['A', 'B', 'C', 'D', 'I', 'H', 'G']

>>> parcours_profondeur_rec(G2, 'D')
['D', 'I', 'H']
    Une piste

    La variable tab est initialisée par défaut à None.
    Il faut tester cette situation et « placer » alors un tableau vide dans cette variable.

Partie D - Distance d'un sommet aux autres☘

En adaptant un des trois algorithmes précédents, complétez la définition de la fonction distances() qui prend en paramètre un graphe et un sommet de ce graphe. Cette fonction renvoie un dictionnaire d'associations {sommet2: distance} où sommet2 est un sommet du graphe et distance est le nombre d'arêtes traversées pour aller de sommet à sommet2.

1
2
3
4
5
6
7
8
def distances(graphe, sommet):
    """
    graphe - Graphe, graphe orienté ou non orienté
    sommet - Un sommet du graphe
    Sortie: dict, dictionnaire d'associations {sommet2: distance} où sommet2 est
            un sommet du graphe et distance est le nombre d'arêtes traversées
            pour aller de sommet à sommet2
    """

Plan de test

>>> distances(G1, 'A')
{'A': 0, 'B': 1, 'D': 1, 'C': 2, 'E': 2, 'F': 2, 'G': 3, 'H': 3}

>>> distances(G1, 'D')
{'D': 0, 'A': 1, 'C': 1, 'E': 1, 'F': 1, 'B': 2, 'G': 2, 'H': 2}

>>> distances(G2, 'A')
{'A': 0, 'B': 1, 'G': 1, 'C': 2, 'H': 2, 'D': 3, 'I': 4}

>>> distances(G2, 'D')
{'D': 0, 'I': 1, 'H': 2}

Partie E - Détection de cycle☘

Complétez la définition de la fonction cycle() qui prend en paramètres un graphe et qui renvoie True s'il existe un cycle dans ce graphe, False sinon.

1
2
3
4
5
6
def cycle(graphe):
    """
    graphe - Graphe, graphe orienté ou non orienté
    Sortie: bool, True si le graphe contient un cycle,
            False sinon
    """

Plan de test

>>> cycle(G1)
True

>>> cycle(G2)
False
Une piste

Vous pouvez définir une fonction récursive detecte_cycle() qui renvoie True s'il existe un cycle sur un chemin parcouru à partir du sommet passé en paramètre.

Une autre piste

Voici des spécifications possibles pour la fonction detecte_cycle() :

1
2
3
4
5
6
7
8
9
def detecte_cycle(graphe, sommet, couleur):
    """
    graphe - Graphe, graphe orienté ou non orienté
    sommet - Un sommet du graphe
    couleur - dict, dictionnaire qui, à chaque sommet du graphe,
                    associe une couleur parmi 'blanc', 'gris' et 'noir'
    Sortie: bool, True si le graphe détecte un cycle en parcourant depuis sommet,
            False sinon
    """

Partie F - Recherche de chemin☘

  1. Complétez la définition de la fonction existe_chemin() qui prend en paramètres un graphe et deux sommets s1 et s2 de ce graphe.
    Elle renvoie True s'il existe un chemin allant de s1 à s2, et False sinon.

    1
2
3
4
5
6
7
    def existe_chemin(graphe, s1, s2):
    """
    graphe - Graphe, graphe orienté ou non orienté
    s1, s2 - Deux sommets du graphe
    Sortie: bool, True s'il existe un chemin allant de s1 à s2,
            False sinon
    """

    Plan de test

    >>> existe_chemin(G1, 'A', 'D')
True

>>> existe_chemin(G1, 'D', 'A')
True

>>> existe_chemin(G2, 'A', 'D')
True

>>> existe_chemin(G2, 'D', 'A')
False

>>> existe_chemin(G2, 'K', 'C')
False

  2. En adaptant un des trois algorithmes de parcours, complétez la définition de la fonction construire_chemin() qui prend en paramètre un graphe et deux sommets s1 et s2 de ce graphe. Cette fonction renvoie, s'il existe, un chemin sous forme de tableau contenant les sommets intermédiaires permettant d'aller de s1 à s2.

    1
2
3
4
5
6
7
    def construire_chemin(graphe, s1, s2):
    """
    graphe - Graphe, graphe orienté ou non orienté
    s1, s2 - Deux sommets du graphe
    Sortie: list, Tableau des sommets traversés pour aller de s1 à s2
            si un tel chemin existe
    """

    Plan de test

    >>> construire_chemin(G1, 'A', 'D')
['A', 'D']

>>> construire_chemin(G1, 'A', 'H')
['A', 'D', 'F', 'H']

>>> construire_chemin(G2, 'F', 'H')
['F', 'E', 'D', 'I', 'H']

>>> construire_chemin(G2, 'D', 'A')
[]
    Une piste

    Au lieu de placer les sommets parcourus dans un tableau, placez-les dans un dictionnaire dont les clefs sont les prédécesseurs des sommets parcourus.