Sudoku et coloriage « glouton »

Le travail présenté dans cette page est basé sur une idée originale de Mesdames MOUGEOT, REYNAUD et MARTENS et de Monsieur JUNIER, enseignants de NSI dans l'académie de Lyon. Que tous les quatre en soient ici remerciés.

Le problème de résolution d’un Sudoku à $n$ chiffres dans une grille $n$ × $n$ est un problème difficile pour lequel il n’existe pas d’algorithme de résolution connu de complexité temporelle polynomiale, c’est-à-dire avec un nombre d’opérations élémentaires inférieur ou égal à $C n^k$ avec $C$ une constante et $k$ un entier naturel.
En revanche, on a vu qu’il est possible de vérifier si une grille de Sudoku est correctement remplie avec une complexité temporelle de l’ordre de la taille de la grille à une constante près.

D’autres questions intéressantes sur les Sudokus sont par exemple le nombre minimum de données pour qu’une grille ait une unique solution. En 2011, des chercheurs ont démontré que ce nombre minimum d’informations nécessaires est de 17 pour un Sudoku à 9 chiffres. On pourra lire sur ce sujet cet article du magazine « Pour la Science ».

Force brute

Dans cette partie, on suppose qu’on essaie de résoudre une grille de Sudoku avec un algorithme « brute force » qui teste toutes les grilles possibles sans examiner les contraintes.

1. Déterminez le nombre de grilles à tester pour résoudre par brute force une grille de Sudoku 9 × 9 dont 36 cases sont initialement fixées.

   Réponse

   Il reste à compléter 45 cases qui ont chacune 9 possibilités.
   Cela donne $9^{45}$ possibilités à tester.

2. Donnez un ordre de grandeur du nombre de jours qu’il faudrait à une machine, capable de tester $10^6$ possibilités par seconde, pour explorer toutes les possibilités déterminées à la question précédente.

   Réponse

   $\frac{9^{45}}{10^6} ≈ 9 × 10^{36}$ secondes, soit environ $10^{32}$ jours !!!

Conséquence

Puisqu’un tel algorithme n’est pas raisonnable, on va utiliser des heuristiques qui sont des méthodes de calcul permettant d’atteindre rapidement une solution et d’échapper à l’explosion combinatoire de l’étude exhaustive de toutes les possibilités.

Première heuristique gloutonne

Dans la première partie, vous avez montré que la résolution d’une grille de Sudoku est équivalente à un problème de coloration de graphe où chaque case/sommet est reliée par une arête aux cases/sommets de la même ligne, de la même colonne ou du même bloc.

La coloration de graphe consiste à attribuer une couleur à chacun des sommets du graphe de sorte que deux sommets reliés par une arête soient de couleur différente. On cherche souvent à utiliser le moins de couleurs possibles.

Dans la suite, on travaille sur une instance de la classe Sudoku construite à la fin de la deuxième partie. On nomme cette instance sudo :

sudo = Sudoku()

Cette classe contient une méthode .generer_graphe() qui initialise l’attribut adj. Ainsi sudo.adj est une liste de listes (un tableau de tableaux) qui permet d’obtenir, pour chaque case/sommet, la liste de ses voisins c’est-à-dire le tableau des cases/sommets dans une même ligne, une même colonne ou un même bloc.

Voici une description d’une première heuristique gloutonne de coloriage en pseudo-code :

Étape 1 :
- Avec la méthode conversion_grille_vers_couleur, on initialise une liste couleur,
  de taille le nombre total de cases, avec les couleurs déjà fixées (de 1 à nbCouleur)
  et 0 sinon ;
- On initialise une variable nombreAcolorier avec le nombre de cases/sommets non coloriés
  dans la liste couleur (soit le nombre de cases telles que couleur[case] == 0) ;
- On initialise case à 0.

Étape 2 :
- À partir de la case courante, si elle n’a pas de couleur (couleur[case] == 0),
  on initialise une variable couleurs_possibles avec la liste de toutes les couleurs possibles ;
- On réalise une boucle sur les voisins grâce à l’attribut adj et, pour chaque voisin,
  on enlève la couleur du voisin si elle fait partie de la liste couleurs_possibles ;
- Ensuite si couleurs_possibles est non vide, on fixe la couleur de case en choisissant
  aléatoirement une couleur parmi couleurs_possibles et on décrémente nombreAcolorier de 1 ;
- On incrémente case de 1 ;
- Si toutes les cases de la grille n’ont pas été visitées (case < nbcases) et
  si toutes les cases ne sont pas encore coloriées (nombreAcolorier > 0), on reprend
  à l’étape 2, sinon on passe à l’étape 3.

Étape 3 :
- Si nombreAcolorier est égal à 0, on a trouvé une solution : on a colorié toutes les cases/sommets,
  la grille est remplie et on a terminé.

1. Que pensez-vous a priori de cet algorithme ?

   Une réponse

   Il est clair que cette heuristique simpliste ne permet pas, en général, de résoudre une grille !

2. Pour quels types de Sudoku pensez-vous qu’il pourrait être efficace ?

   Une réponse

   La résolution pourrait être efficace avec des sudoku 2 × 2, ou 3 × 3, avec beaucoup de couleurs déjà données.

3. On a qualifié cette heuristique de « gloutonne ».
   Quels choix sont effectués lors de l’étape 2 ?

   Une réponse

   On choisit une couleur au hasard parmi les possibles, on prend les sommets dans l’ordre...

Répétition de l'heuristique gloutonne

Une idée d'amélioration consiste à recommencer toutes les étapes depuis le début si on n’a pas colorié toutes les cases. En effet, comme le choix de la couleur à l’étape 2 est aléatoire, chaque exécution de l’heuristique peut être différente et on peut espérer trouver une solution « par hasard ».
On parle dans ce cas d’algorithme randomisé. On peut ainsi fixer un nombre maximum itermax d’itérations de l’heuristique et retourner la grille solution dès qu’on l’a trouvée (sortie prématurée) avec la méthode .conversion_couleur_vers_grille() ou None si on a épuisé toutes les tentatives sans résoudre le problème.

1. Téléchargez le fichier sudoku_heuristique_gloutonne.py.

2. Implémentez l'heuristique gloutonne détaillée dans le paragraphe précédent.
   Pour cela, complétez le corps de la fonction resolution_sudoku_coloration_glouton(), qui est une méthode membre de la classe Sudoku.

   def resolution_sudoku_coloration_glouton(self, grille, itermax,  *args, **kwargs):
       """on parcourt la grille de la première à la dernière case en choisissant, pour les sommets non colorés,
       une couleur au hasard parmi les possibles"""
       for tentative in range(1, itermax + 1):
           couleur = self.conversion_grille_vers_couleur(grille)
           nombreAcolorier = couleur.count(0)
           #on commence à la première case
           case = 0
   
           ### TO DO à compléter
   
           if nombreAcolorier == 0 :
               return (tentative, self.conversion_couleur_vers_grille(couleur))
   
       return (itermax, None)
   

   Une piste

   Voici un diagramme d’exécution (flowchart) de cet algorithme :

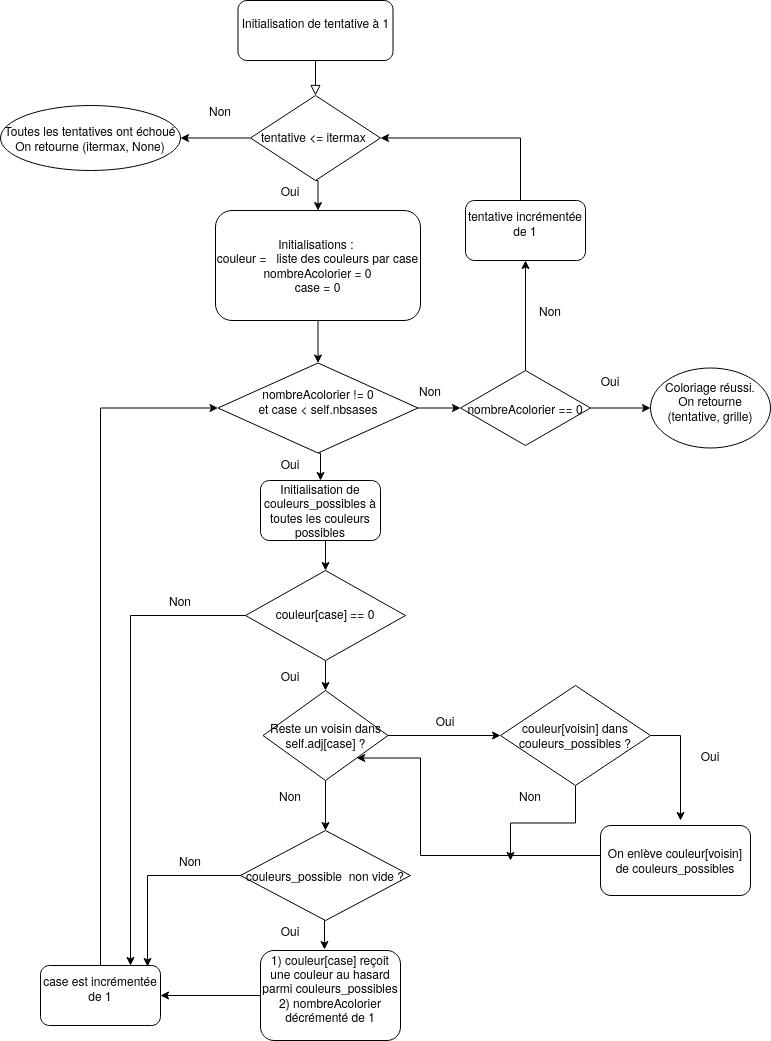
   Une réponse

   def resolution_sudoku_coloration_glouton(self, grille, itermax,  *args, **kwargs):
       """on parcourt la grille de la première à la dernière case en choisissant, pour les sommets non colorés,
       une couleur au hasard parmi les possibles"""
       for tentative in range(1, itermax + 1):
           couleur = self.conversion_grille_vers_couleur(grille)
           nombreAcolorier = couleur.count(0)
           case = 0
           while nombreAcolorier != 0 and case < self.nbcases:  
               if couleur[case] == 0 :
                   couleurs_possibles = list(range(1, self.nbcouleurs + 1))
                   for voisin in self.adj[case] :
                       if couleur[voisin] in couleurs_possibles :
                           couleurs_possibles.remove(couleur[voisin])
                   if couleurs_possibles != [] :
                       couleur[case] = random.choice(couleurs_possibles)
                       nombreAcolorier -= 1
               case += 1
           if nombreAcolorier == 0 :
               return (tentative, self.conversion_couleur_vers_grille(couleur))
   
       return (itermax, None)
   

3. Exécutez le fichier sudoku_heuristique_gloutonne.py pour tester la fonction.
   Elle devrait résoudre la grille 4 × 4 et la première grille 9 × 9 testées dans test_coloration. Les nombres de tentatives sont-ils les mêmes que ceux obtenus par vos camarades ? Pourquoi ?

Amélioration de l'heuristique gloutonne

Dans l’heuristique précédente le choix glouton s’effectuait sur une case fixée en suivant l’ordre des numéros des cases. Il peut sembler pertinent de chercher à optimiser ce choix. Ainsi, on va sélectionner dans une liste liste_candidat les cases à colorier parmi celles qui ont le plus de contraintes, c'est-à-dire celles dont le nombre de couleurs possibles est minimal. On choisira aléatoirement une case à colorier parmi celles-ci.

On obtient alors une heuristique randomisée de coloriage que nous pourrons itérer comme la précédente jusqu’au coloriage de toutes les cases (sortie prématurée) ou jusqu’à l’épuisement du nombre maximal itermax d’itérations.

1. Dans le fichier sudoku_heuristique_gloutonne.py, complétez la définition de la fonction resolution_sudoku_coloration_glouton_tri1() qui est une méthode membre de la classe Sudoku.

   Le code à compléter

   def resolution_sudoku_coloration_glouton_tri1(self, grille, itermax):
       '''Résolution de sudoku par  coloration de graphe 
       voir http://www.cs.kent.edu/~dragan/ST-Spring2016/SudokuGC.pdf '''
   
   
       def resolution():
           """Fonction de résolution de Sudoku par heuristique gloutonne randomisée"""
           #on récupère la liste des couleurs de chaque sommet/case
           couleur = self.conversion_grille_vers_couleur(grille)
           #liste des cases/sommets  à traiter (leur couleur n'est pas encore fixée)
           caseAFaire  = [case for case in range(self.nbcases)]   
           #liste des couleurs possibles pour chaque case   
           liste_couleur_possible = [ list(range(1, self.nbcouleurs + 1))  for case in range(self.nbcases)]
           #on initialise les cases dont les couleurs sont déjà fixées
           for case, color  in enumerate(couleur):
               #on fixe la couleur des cases déjà coloriées
               if color > 0:
                   liste_couleur_possible[case] = [color]     
           #tant qu'il y a des cases à traiter 
           while len(caseAFaire) > 0: 
               #liste des candidats à compléter           
               liste_candidat = []
               nbcouleur_min = self.nbcouleurs + 1
               #on sélectionne d'abord les sommets non traités qui ont le moins de couleurs possibles
   
   
               #### TO DO à compléter
               "à compléter "
   
               if len(liste_candidat) == 0:   #à commenter après avoir complété
                   return None                #à commenter après avoir complété
   
               #si on a trouvé des sommets pour lesquels il ne reste plus qu'une seule couleur possible
               #ce sont ces sommets qu'on va colorier et on ne change pas liste_candidat
               #sinon on en choisit un au hasard parmi liste_candidat
               if nbcouleur_min != 1:                    
                   liste_candidat = [random.choice(liste_candidat)]                            
               #il reste à fixer la couleur des sommets dans liste_candidat
               #et à propager la contrainte sur leurs voisins                                       
               for case in liste_candidat:                    
                   if len(liste_couleur_possible[case]) == 0 : 
                       #plus de couleurs disponibles pour la case à colorier
                       #dans ce cas le coloriage ne fonctionne pas 
                       return  None
   
                   #il faut enlever une couleur de liste_couleur_possible[case]
                   #puis mettre à jour liste_couleur_possible[voisin] pour tous les voisins 
                   #et sortir case de la liste caseAFaire
   
                   #### TO DO à compléter
                   "à compléter "
   
           #fini grille résolue
           return self.conversion_couleur_vers_grille(couleur)      
   
       #comme l'algorithme de coloriage est randomisé
       # on tente des essais successifs tant qu'on n'a pas résolu la grille
       # avec un nombre maximal d'itérations
       for k in range(1, itermax):
           solution= resolution()
           if solution is not None:
               return (k, solution)
       return  (itermax, None)
   

   Une piste

   Voici un diagramme d’exécution (flowchart) de cet algorithme :

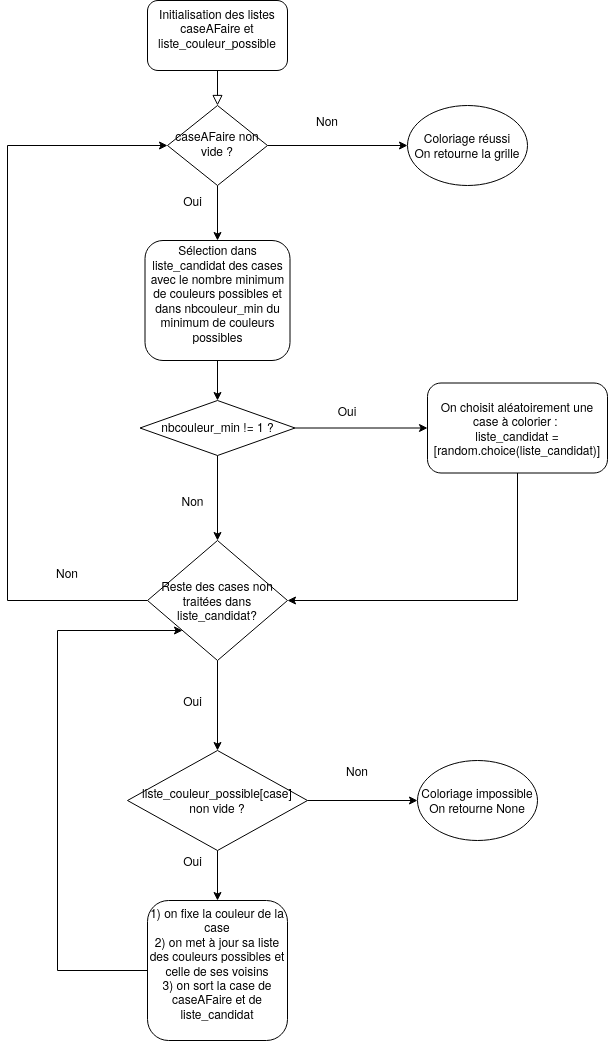
   Une réponse

   def resolution_sudoku_coloration_glouton_tri1(self, grille, itermax):
       '''Résolution de sudoku par  coloration de graphe 
       voir http://www.cs.kent.edu/~dragan/ST-Spring2016/SudokuGC.pdf '''
   
   
       def resolution():
           """Fonction de résolution de Sudoku par heuristique gloutonne randomisée"""
           #on récupère la liste des couleurs de chaque sommet/case
           couleur = self.conversion_grille_vers_couleur(grille)
           #liste des cases/sommets  à traiter (leur couleur n'est pas encore fixée)
           caseAFaire  = [case for case in range(self.nbcases)]   
           #liste des couleurs possibles pour chaque case   
           liste_couleur_possible = [ list(range(1, self.nbcouleurs + 1))  for case in range(self.nbcases)]
           #on initialise les cases dont les couleurs sont déjà fixées
           for case, color  in enumerate(couleur):
               #on fixe la couleur des cases déjà coloriées
               if color > 0:
                   liste_couleur_possible[case] = [color]     
           #tant qu'il y a des cases à traiter 
           while len(caseAFaire) > 0: 
               #liste des candidats à compléter           
               liste_candidat = []
               nbcouleur_min = self.nbcouleurs + 1
               #on sélectionne d'abord les sommets non traités qui ont le moins de couleurs possibles
               #on sélectionne d'abord les sommets non traités qui ont le moins de couleurs possibles
               for case in caseAFaire:
                   #nombre de couleurs possibles pour le sommet
                   nbcouleur = len(liste_couleur_possible[case])
                   #mise à jour du minimum nbcouleurmin
                   if  nbcouleur < nbcouleur_min:
                       liste_candidat = [case]
                       nbcouleur_min = nbcouleur
                   elif nbcouleur == nbcouleur_min:
                       liste_candidat.append(case)
   
   
               #si on a trouvé des sommets pour lesquels il ne reste plus qu'une seule couleur possible
               #ce sont ces sommets qu'on va colorier et on ne change pas liste_candidat
               #sinon on en choisit un au hasard parmi liste_candidat
               if nbcouleur_min != 1:                    
                   liste_candidat = [random.choice(liste_candidat)]                            
               #il reste à fixer la couleur des sommets dans liste_candidat
               #et à propager la contrainte sur leurs voisins                                       
               for case in liste_candidat:                    
                   if len(liste_couleur_possible[case]) == 0 : 
                       #plus de couleurs disponibles pour la case à colorier
                       #dans ce cas le coloriage ne fonctionne pas 
                       return  None
   
                   #il faut enlever une couleur de liste_couleur_possible[case]
                   #puis mettre à jour liste_couleur_possible[voisin] pour tous les voisins 
                   #et sortir case de la liste caseAFaire
   
                   couleur[case] =   liste_couleur_possible[case].pop()
                   for voisin in self.adj[case]:
                       if couleur[case] in liste_couleur_possible[voisin]:
                           liste_couleur_possible[voisin].remove(couleur[case])
                   caseAFaire.remove(case)  
   
           #fini grille résolue
           return self.conversion_couleur_vers_grille(couleur)      
   
       #comme l'algorithme de coloriage est randomisé
       # on tente des essais successifs tant qu'on n'a pas résolu la grille
       # avec un nombre maximal d'itérations
       for k in range(1, itermax):
           solution= resolution()
           if solution is not None:
               return (k, solution)
       return  (itermax, None)
   

2. Exécutez le fichier sudoku_heuristique_gloutonne.py comparez les résultats obtenus par les fonctions resolution_sudoku_coloration_glouton() et resolution_sudoku_coloration_glouton_tri1().

3. On propose d’écrire une fonction resolution_sudoku_coloration_glouton_tri() similaire à la précédente, mais avec deux variantes supplémentaires au niveau du choix de la prochaine case à colorier :
   a. en sélectionnant parmi les cases qui ont le plus de contraintes, c’est-à-dire dans la liste liste_candidat, celles qui ont le moins de voisins non coloriés ;
   b. en sélectionnant parmi les cases qui ont le plus de contraintes, c’est-à-dire dans la liste liste_candidat, celles qui ont le plus de voisins non coloriés.
   Le paramètre version de la fonction resolution_sudoku_coloration_glouton_tri() permettra de sélectionner l’une des trois variantes de l’heuristique.
   Implémentez cette fonction en complétant les parties signalées par des commentaires #### TO DO à compléter dans le fichier sudoku_heuristique_gloutonne.py.
   Cette méthode membre de la classe Sudoku contient trois fonctions outils plus_petit(), plus_grand() et selection_extremum_voisins() qu’il faut compléter en respectant la spécification donnée dans la documentation.

   Le code à compléter

   def resolution_sudoku_coloration_glouton_tri(self, grille, itermax, version):
       '''Résolution de sudoku par  coloration de graphe 
       voir http://www.cs.kent.edu/~dragan/ST-Spring2016/SudokuGC.pdf '''
       #version 'moins' : on choisit au hasard parmi ceux qui ont le moins de voisins non coloriés (couleur[voisin] == 0)      
       #version 'plus' : on choisit au hasard parmi ceux qui ont le plus de voisins non coloriés (couleur[voisin] == 0)
       #version 'hasard' : pas de tri préalable
   
       def plus_petit(a, b):
           """Retourne True si a < b et False sinon"""
           return a < b
   
       def plus_grand(a, b):
           """Retourne True si a > b et False sinon"""
           #### TO DO à compléter
           "à compléter"
   
       def selection_extremum_voisins(liste_candidat, couleur, valeur_initiale = float('inf'), comparaison = plus_petit):
           """Fonction qui retourne une case choisie aléatoirement parmi les cases dans liste_candidat
           telles que le nombre de voisins non coloriés est minimal (valeur_initiale = float('inf'), comparaison = plus_petit)
           ou maximal (valeur_initiale = 0, comparaison = plus_grand)
           """
           nb_voisins_blancs_extremum = valeur_initiale
           case_record = []
           for case in liste_candidat:
               nb_voisins_blancs = 0
               for voisin in self.adj[case]:
                   if couleur[voisin] == 0:
   
                       #### TO DO à compléter
                       "à compléter "
   
               if comparaison(nb_voisins_blancs,  nb_voisins_blancs_extremum):
   
                   #### TO DO à compléter
                   "à compléter "
   
               elif nb_voisins_blancs == nb_voisins_blancs_extremum:
   
                   #### TO DO à compléter
                   "à compléter "
   
           #choix aléatoire
           return [random.choice(case_record)]
   
       def resolution():
           """Fonction de résolution de Sudoku par heuristique gloutonne randomisée"""
           #on récupère la liste des couleurs de chaque sommet/case
           couleur = self.conversion_grille_vers_couleur(grille)
           #liste des cases/sommets  à traiter (leur couleur n'est pas encore fixée)
           caseAFaire  = [case for case in range(self.nbcases)]   
           #liste des couleurs possibles pour chaque case   
           liste_couleur_possible = [ list(range(1, self.nbcouleurs + 1))  for case in range(self.nbcases)]
           #on initialise les cases dont les couleurs sont déjà fixées
           for case, color  in enumerate(couleur):
               #on fixe la couleur des cases déjà coloriées
               if color > 0:
                   liste_couleur_possible[case] = [color]     
           #tant qu'il y a des cases à traiter 
           while len(caseAFaire) > 0: 
               #liste des candidats à compléter           
               liste_candidat = []
               nbcouleur_min = self.nbcouleurs + 1
               #on sélectionne d'abord les sommets non traités qui ont le moins de couleurs possibles
   
   
               #### TO DO à compléter
               "à compléter "
   
               if len(liste_candidat) == 0:   #à commenter après avoir complété
                   return None                #à commenter après avoir complété
   
               #si on a trouvé des sommets pour lesquels il ne reste plus qu'une seule couleur possible
               #ce sont ces sommets qu'on va colorier et on ne change pas liste_candidat
               #sinon on distingue trois cas
               if nbcouleur_min != 1:                    
                   #premier cas : on choisit parmi les sommets  dans liste_candidat
                   #ceux qui ont le moins   de voisins non coloriés
                   if version == 'moins' :
                       liste_candidat = selection_extremum_voisins(liste_candidat, couleur, valeur_initiale = 0, comparaison = plus_grand)
                   #deuxième cas : on choisit parmi les sommets  dans liste_candidat
                   #ceux qui ont le plus  de voisins non coloriés
                   elif version == 'plus' :                      
                       liste_candidat = selection_extremum_voisins(liste_candidat, couleur, valeur_initiale = float('inf'), comparaison = plus_petit)
                   #troisième cas : on choisit au hasard parmi les sommets  dans liste_candidat
                   else :
                       liste_candidat = [random.choice(liste_candidat)]                            
               #il reste à fixer la couleur des sommets dans liste_candidat
               #et à propager la contrainte sur leurs voisins                                       
               for case in liste_candidat:                    
                   if len(liste_couleur_possible[case]) == 0 : 
                       #plus de couleurs disponibles pour la case à colorier
                       #dans ce cas le coloriage ne fonctionne pas 
                       return  None
   
                   #il faut enlever une couleur de liste_couleur_possible[case]
                   #puis mettre à jour liste_couleur_possible[voisin] pour tous les voisins 
                   #et sortir case de la liste caseAFaire
   
                   #### TO DO à compléter
                   "à compléter "
   
           #fini grille résolue
           return self.conversion_couleur_vers_grille(couleur)      
   
       #comme l'algorithme de coloriage est randomisé
       # on tente des essais successifs tant qu'on n'a pas résolu la grille
       # avec un nombre maximal d'itérations
       for k in range(1, itermax):
           solution= resolution()
           if solution is not None:
               return (k, solution)
       return  (itermax, None)
   

   Une réponse

   def resolution_sudoku_coloration_glouton_tri(self, grille, itermax, version,  *args, **kwargs):
       '''Résolution de sudoku par  coloration de graphe 
       voir http://www.cs.kent.edu/~dragan/ST-Spring2016/SudokuGC.pdf '''
       #version 'moins' : on choisit au hasard parmi ceux qui ont le moins de voisins non coloriés (couleur[voisin] == 0)      
       #version 'plus' : on choisit au hasard parmi ceux qui ont le plus de voisins non coloriés (couleur[voisin] == 0)
       #version 'hasard' : pas de tri préalable
   
       def plus_petit(a, b):
           return a < b
   
       def plus_grand(a, b):
           return a > b
   
       def selection_extremum_voisins(liste_candidat, couleur, valeur_initiale = float('inf'), comparaison = plus_petit):
           """Fonction qui retourne une case choisie aléatoirement parmi les cases dans liste_candidat
           telles que le nombre de voisins non coloriés est minimal (valeur_initiale = float('inf'), comparaison = plus_petit)
           ou maximal (valeur_initiale = 0, comparaison = plus_grand)
           """
           nb_voisins_blancs_extremum = valeur_initiale
           case_record = []
           for case in liste_candidat:
               nb_voisins_blancs = 0
               for voisin in self.adj[case]:
                   if couleur[voisin] == 0:
                       nb_voisins_blancs += 1
               if comparaison(nb_voisins_blancs,  nb_voisins_blancs_extremum):
                   nb_voisins_blancs_extremum  =  nb_voisins_blancs
                   case_record = [case]
               elif nb_voisins_blancs == nb_voisins_blancs_extremum:
                   case_record.append(case)
           #choix aléatoire
           return [random.choice(case_record)]
   
       def resolution():
           """Fonction de résolution de Sudoku par heuristique gloutonne randomisée"""
           #on récupère la liste des couleurs de chaque sommet/case
           couleur = self.conversion_grille_vers_couleur(grille)
           #liste des cases/sommets  à traiter (leur couleur n'est pas encore fixée)
           caseAFaire  = [case for case in range(self.nbcases)]   
           #liste des couleurs possibles pour chaque case   
           liste_couleur_possible = [ list(range(1, self.nbcouleurs + 1))  for case in range(self.nbcases)]
           #on initialise les cases dont les couleurs sont déjà fixées
           for case, color  in enumerate(couleur):
               #on fixe la couleur des cases déjà coloriées
               if color > 0:
                   liste_couleur_possible[case] = [color]     
           #tant qu'il y a des cases à traiter 
           while len(caseAFaire) > 0: 
               #liste des candidats à compléter           
               liste_candidat = []
               nbcouleur_min = self.nbcouleurs + 1
               #on sélectionne d'abord les sommets non traités qui ont le moins de couleurs possibles
               for case in caseAFaire:
                   #nombre de couleurs possibles pour le sommet
                   nbcouleur = len(liste_couleur_possible[case])
                   #mise à jour du minimum nbcouleurmin
                   if  nbcouleur < nbcouleur_min:
                       liste_candidat = [case]
                       nbcouleur_min = nbcouleur
                   elif nbcouleur == nbcouleur_min:
                       liste_candidat.append(case)
               #si on a trouvé des sommets pour lesquels il ne reste plus qu'une seule couleur possible
               #ce sont ces sommets qu'on va colorier et on ne change pas liste_candidat
               #sinon on distingue trois cas               
               if nbcouleur_min > 1:                    
                   #premier cas : on choisit parmi les sommets  dans liste_candidat
                   #ceux qui ont le moins   de voisins non coloriés
                   if version == 'moins' :
                       liste_candidat = selection_extremum_voisins(liste_candidat, couleur, valeur_initiale = 0, comparaison = plus_grand)
                   #deuxième cas : on choisit parmi les sommets  dans liste_candidat
                   #ceux qui ont le plus  de voisins non coloriés
                   elif version == 'plus' :                      
                       liste_candidat = selection_extremum_voisins(liste_candidat, couleur, valeur_initiale = float('inf'), comparaison = plus_petit)
                   #troisième cas : on choisit au hasard parmi les sommets  dans liste_candidat
                   else :
                       liste_candidat = [random.choice(liste_candidat)]                            
               #il reste à fixer la couleur des sommets dans liste_candidat
               #et à propager la contrainte sur leurs voisins                                       
               for case in liste_candidat:                    
                   if len(liste_couleur_possible[case]) == 0 : 
                       #plus de couleurs disponibles pour la case à colorier
                       #dans ce cas le coloriage ne fonctionne pas 
                       return  None
                   couleur[case] =   liste_couleur_possible[case].pop()
                   for voisin in self.adj[case]:
                       if couleur[case] in liste_couleur_possible[voisin]:
                           liste_couleur_possible[voisin].remove(couleur[case])
                   caseAFaire.remove(case)  
           #fini grille résolue
           return self.conversion_couleur_vers_grille(couleur)      
   
       #comme l'algorithme de coloriage est randomisé
       # on tente des essais successifs tant qu'on n'a pas résolu la grille
       # avec un nombre maximal d'itérations
       for k in range(1, itermax):
           solution= resolution()
           if solution is not None:
               return (k, solution)
       return  (itermax, None)
   

4. Exécutez le fichier sudoku_heuristique_gloutonne.py, tous les tests contenus dans les fonctions test_coloration() et test_diabolique() devraient être réalisés.
   Comparez et commentez les résultats obtenus par les différentes heuristiques.