Le graphe Sudoku☘
Le sudoku est un jeu en forme de grille défini en 1979 par l’Américain Howard Garns, mais inspiré du carré latin, ainsi que du problème des 36 officiers du mathématicien suisse Leonhard Euler.
Le but du jeu est de remplir la grille avec une série de chiffres (ou de lettres ou de symboles) tous différents, qui ne se trouvent jamais plus d’une fois sur une même ligne, dans une même colonne ou dans une même région (également appelée « bloc », « groupe », « secteur » ou « sous-grille »). La plupart du temps, les symboles sont des chiffres allant de 1 à 9, les régions étant alors des carrés de 3 × 3. Quelques symboles sont déjà disposés dans la grille, ce qui autorise une résolution progressive du problème complet.
Pour s'échauffer☘
Tentez de résoudre les 2 grilles de Sudoku de 2×2 ci-dessous :
-
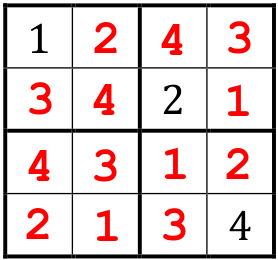
Grille n°1
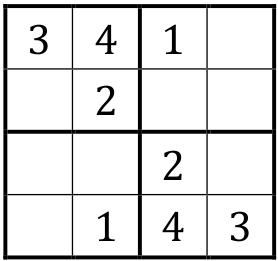
Une solution
-
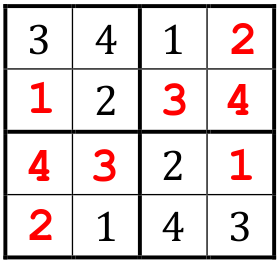
Grille n°2
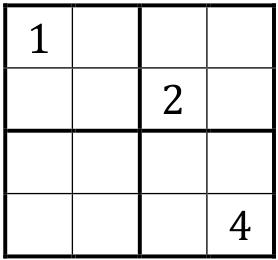
Une solution
Plusieurs solutions sont possibles avec cette grille. En voici une :
Le graphe Sudoku☘
Convention
Afin de faciliter la manipulation, les grilles seront au format 2 × 2 dans les questions. Toutefois, il ne faut pas oublier que le but des questions est ensuite de généraliser au format 3 × 3, 4 × 4, etc...
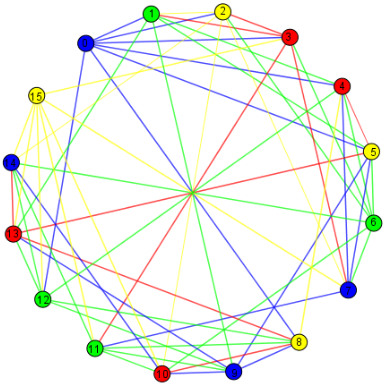
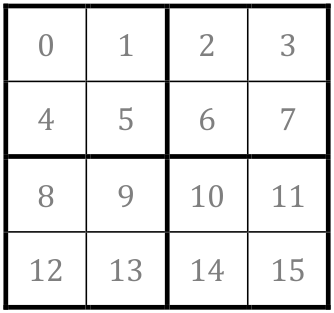Afin de représenter le Sudoku sous forme de graphe non orienté, nous allons
considérer que les sommets du graphe sont les cases du Sudoku, numérotées de
0 à 15 en allant de gauche à droite et de haut en bas, comme sur la figure
ci-contre.
Chaque arête du graphe est placée entre deux sommets liés par une contrainte.
Exemple
La case 0 est liée à toutes les cases de sa ligne car, sur une même ligne,
il ne peut pas y avoir deux fois le même chiffre.
Cette case est aussi liée à toutes les cases de sa colonne et à toutes
celles de sa région.
Afin d’éviter toutes confusions entre les numéros de cases (de 0 à 15) et
les valeurs de celles-ci (entre 1 et 4), nous allons raisonner avec des
couleurs : {1 : 'bleu', 2 : 'vert', 3 : 'rouge', 4 : 'jaune'}.
Ainsi, la première grille :
devient
-
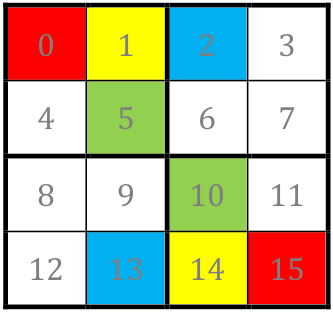
Quel sera le degré de chaque sommet ?
Une réponse
Chaque sommet est lié à trois autres sur sa ligne, à trois autres sur sa colonne et à un dernier non encore sélectionné dans sa région, soit 7 arêtes par sommet.
Chaque sommet est donc de degré 7. -
Recopiez et complétez le graphe ci-dessous en ajoutant les arêtes pour chaque sommet.
-
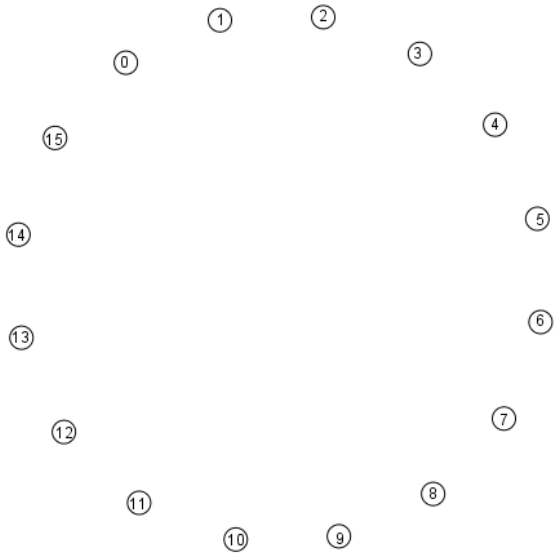
Coloriez les sommets dont on connait la couleur.
-
Ajoutez, à côté de chaque sommet qui n’a pas de couleur, le nombre de sommets de couleurs différentes avec lesquels il est en relation.
Une réponse
-
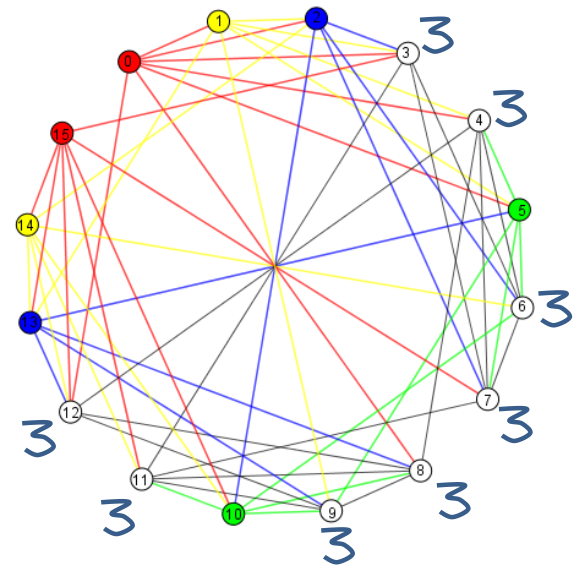
A votre avis, par quel sommet peut-on commencer le remplissage ?
Une réponse
N'importe lequel convient ici.
-
Téléchargez le fichier graphe-sudoku.ggb.
En utilisant ce fichier, essayez de résoudre la grille n°2 de la même manière :Une réponse
On ajoute, à côté de chaque sommet qui n’a pas de couleur, le nombre de sommets de couleurs différentes avec lesquels il est en relation :
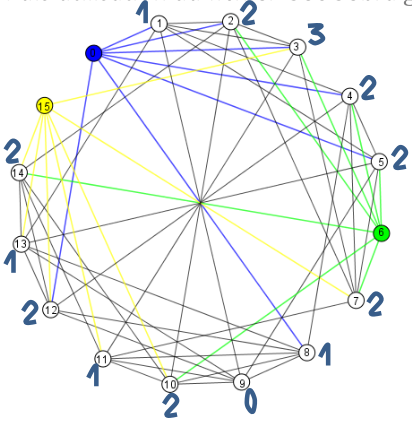
On commence par le sommet n°3, pour lequel ce nombre est le plus grand :
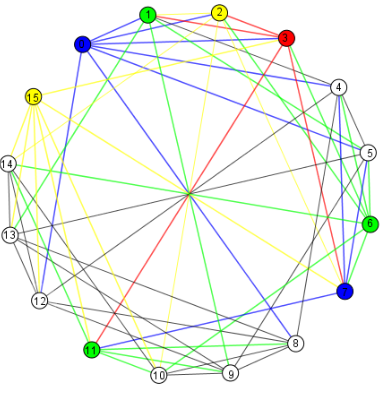
On termine :
