Sudoku et POO

Le travail présenté dans cette page est basé sur une idée originale de Mesdames MOUGEOT, REYNAUD et MARTENS et de Monsieur JUNIER, enseignants de NSI dans l'académie de Lyon. Que tous les quatre en soient ici remerciés.

Un sudoku est défini par sa taille $n$ qui est le nombre de blocs sur une ligne (ou une colonne).
Il utilise un tableau à deux dimensions de taille $n^2 \times n^2$ pour stocker les chiffres contenus dans chaque case.

Dans la page précédente, nous avons numéroté les cases du sudoku de $0$ à $\left(n^2 \times n^2\right) - 1$.
Chaque case du sudoku est considérée comme le sommet d’un graphe.

Puisque les étiquettes des sommets sont des entiers consécutifs, au lieu de stocker la liste des voisins des sommets du graphe dans un dictionnaire, on choisit de stocker cette liste dans un tableau contenant $n^2 \times n^2$ sous-tableaux. Ainsi, Le sous-tableau d’indice $i$, avec $0 ≤ i ≤ \left(n^2 \times n^2\right) - 1$, contient les numéros des sommets qui sont liés par une contrainte avec le sommet d'étiquette $i$.

Exemple

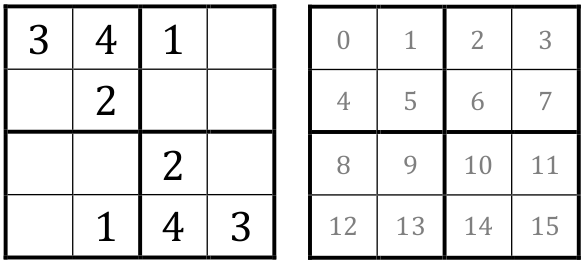On considère la grille de sudoku $2 \times 2$ ci-contre.
Alors :

• Sa taille est $n$ = 2.
• Les sommets sont numérotés de 0 à 15.
• Les couleurs données au départ sont stockées dans le tableau :

  [ [3,4,1,0],
    [0,2,0,0], 
    [0,0,2,0], 
    [0,1,4,3] ]
  

Papier - Crayon

1. Pour un sudoku $2 \times 2$ dont les sommets sont 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 et 15 :

   1. Quels sont les numéros des sommets sur la même ligne que le sommet 0 ?
   2. Quels sont les numéros des sommets sur la même colonne que le sommet 0 ?
   3. Quels sont les numéros des sommets dans le même bloc que le sommet 0 ?
   Réponse

   a. 1, 2, 3
   b. 4, 8, 12
   c. 1, 4, 5

2. Pour un sudoku $2 \times 2$, écrire (au moins le début de) la liste des voisins du graphe des contraintes pour les sommets du sudoku.

   Réponse

   [ [1, 2, 3, 4, 5, 8, 12],
     [0, 2, 3, 4, 5, 9, 13],
     [0, 1, 3, 6, 7, 10, 14],
     [0, 1, 2, 6, 7, 11, 15],
     [0, 1, 5, 6, 7, 8, 12],
     [0, 1, 4, 6, 7, 9, 13],
     [2, 3, 4, 5, 7, 10, 14],
     [2, 3, 4, 5, 6, 11, 15],
     [0, 4, 9, 10, 11, 12, 13],
     [1, 5, 8, 10, 11, 12, 13],
     [2, 6, 8, 9, 11, 14, 15],
     [3, 7, 8, 9, 10, 14, 15],
     [0, 4, 8, 9, 13, 14, 15],
     [1, 5, 8, 9, 12, 14, 15],
     [2, 6, 10, 11, 12, 13, 15],
     [3, 7, 10, 11, 12, 13, 14] ]
   

3. Pour un sudoku $3 \times 3$ :

   1. Quels sont les numéros des sommets sur la même ligne que le sommet 9 ?
   2. Quels sont les numéros des sommets sur la même colonne que le sommet 9 ?
   3. Quels sont les numéros des sommets dans le même bloc que le sommet 9 ?
   Réponse

   a. 10, 11, 12, 13, 14, 15, 16, 17
   b. 0, 18, 27, 36, 45, 54, 63, 72
   c. 0, 1, 2, 10, 11, 18, 19, 20

4. On considère dans cette question un sudoku de taille $n$ et un sommet de numéro $i$.
   Lorsqu’on connait le numéro d’un sommet (entre $0$ et $n^4 − 1$), on peut calculer les indices de sa ligne et de sa colonne dans le sudoku en utilisant la division euclidienne du numéro du sommet par le nombre de couleurs possibles $n^2$.

   1. Pour un sommet $i$, écrire un calcul qui donne l’indice de sa ligne.

      Réponse

      $ligne(i) = i // n^2$

   2. Pour un sommet $i$, écrire un calcul qui donne l’indice de sa colonne.

      Réponse

      $colonne(i) = i$ % $n^2$

   3. Pour un sommet $i$, écrire une formule qui donne les numéros de tous ses voisins en ligne.

      Réponse

      $ligne(i) \times n^2 + k$ pour $k$ allant de $0$ à $n^2 − 1$ et $k ≠ colonne(i)$

   4. Pour un sommet $i$, écrire une formule qui donne les numéros de tous ses voisins en colonne.

      Réponse

      $colonne(i) + n^2 \times k$ pour $k$ allant de $0$ à $n^2 − 1$ et $k ≠ ligne(i)$

   5. Pour un sommet $i$, écrire des calculs qui donnent les indices, entre $0$ et $n − 1$, de la « ligne » et la « colonne » du bloc auquel ce sommet appartient.

      Réponse

      $ligne(bloc) = ligne(i)//n$ et $colonne(bloc) = colonne(i)//n$

   6. Pour un sommet $i$, écrire une formule qui donne le numéro du premier sommet (haut-gauche) qui est dans le même bloc que le sommet $i$.

      Réponse

      $deb(bloc) = (ligne(i)//n) \times n^3 + (colonne(i)//n) × n$

   7. Pour un sommet $i$, écrire une formule qui donnent les numéros des sommets qui sont dans le même bloc.

      Réponse

      $deb(bloc) + c + d \times n^2$ pour $c$ allant de $0$ à $n − 1$ et pour d allant de $0$ à $n − 1$, sans être égal à $i$ !!!

Des fonctions auxiliaires

Important

Téléchargez puis sauvegardez dans votre répertoire courant le fichier graphe_sudoku.py à compléter

Dans cette partie, vous allez coder quelques fonctions utiles pour construire le graphe des contraintes.

1. Complétez la définition de la fonction liste_voisins_ligne() qui reçoit en entrée :

   • un entier n strictement positif qui représente la taille d’un sudoku (n vaut 2 ou 3) ;
   • un entier case compris entre 0 et (n⁴ − 1) qui représente un sommet du sudoku de taille n.

   def liste_voisins_ligne(n, case):
       """Retourne les numéros des cases sur la même ligne de la grille"""
       nbcouleurs = n**2
       #TODO
       return []
   

   La fonction doit renvoyer la liste des sommets du sudoku qui sont sur la même ligne que le sommet case.
   Une réponse

   def liste_voisins_ligne(n, case):
       """Retourne les numéros des cases sur la même ligne de la grille"""
       nbcouleurs = n**2
       lig_case = case // nbcouleurs
       col_case = case % nbcouleurs
       return [lig_case * nbcouleurs + k for k in range(nbcouleurs) if k != col_case]
   

2. Complétez la définition de la fonction liste_voisins_colonne() qui reçoit en entrée :

   • un entier n strictement positif qui représente la taille d’un sudoku (n vaut 2 ou 3) ;
   • un entier case compris entre 0 et (n⁴ − 1) qui représente un sommet du sudoku de taille n.

   def liste_voisins_colonne(n, case):
       """Retourne les numéros des cases sur la même colonne de la grille"""
       nbcouleurs = n**2
       #TODO
       return []
   

   La fonction doit renvoyer la liste des sommets du sudoku qui sont sur la même colonne que le sommet case.
   Une réponse

   def liste_voisins_ligne(n, case):
       """Retourne les numéros des cases sur la même ligne de la grille"""
       nbcouleurs = n**2
       lig_case = case // nbcouleurs
       col_case = case % nbcouleurs
       return [col_case + nbcouleurs * k for k in range(nbcouleurs) if k != lig_case]
   

3. Complétez la définition de la fonction liste_voisins_bloc() qui reçoit en entrée :

   • un entier n strictement positif qui représente la taille d’un sudoku (n vaut 2 ou 3) ;
   • un entier case compris entre 0 et (n⁴ − 1) qui représente un sommet du sudoku de taille n.

   def liste_voisins_bloc(n, case):
       """Retourne les numéros des cases dans le même sous bloc carré"""
       #on détermine la ligne et la colonne du bloc carré correspondant avec lig_case//n et col_case//n
       #dans chaque chaque ligne de blocs, il y a n * nbcouleurs valeurs
       #dans chaque bloc, il y a n colonnes
       nbcouleurs = n**2
       lig_case = case // nbcouleurs
       col_case = case % nbcouleurs
       deb_case = (lig_case // n) * n * nbcouleurs + (col_case // n) * n
       bloc = []
       #TODO
       return bloc
   

   La fonction doit renvoyer la liste des sommets du sudoku qui sont dans le même bloc que le sommet case.
   Une réponse

   def liste_voisins_bloc(n, case):
       """Retourne les numéros des cases dans le même sous bloc carré"""
       #on détermine la ligne et la colonne du bloc carré correspondant avec lig_case//n et col_case//n
       #dans chaque chaque ligne de blocs, il y a n * nbcouleurs valeurs
       #dans chaque bloc, il y a n colonnes
       nbcouleurs = n**2
       lig_case = case // nbcouleurs
       col_case = case % nbcouleurs
       deb_case = (lig_case // n) * n * nbcouleurs + (col_case // n) * n
       bloc = []
       for c in range(n) :
           for d in range(n) :
               autre_case = deb_case + c  + d  * nbcouleurs
               if autre_case != case :
                   bloc.append(autre_case)
       return bloc
   

Génération du graphe des contraintes

Complétez la définition de la fonction generer_graphe() qui reçoit en entrée un entier n strictement positif qui représente la taille d’un sudoku (n vaut 2 ou 3).

def generer_graphe(n) :
    """génère le graphe des contraintes sous la forme d'un tableau"""
    #adj[sommet] correspond à la listes des sommets qui ne doivant pas avoir la même couleur que lui
    nbcases = n**4
    adj = [[] for i in range(nbcases)]
    for case in range(nbcases):
        #TODO
        None
    return adj

La fonction doit renvoyer la liste des voisins du graphe des contraintes pour les sommets du sudoku.

Une réponse

def generer_graphe(n) :
    """génère le graphe des contraintes sous la forme d'un tableau"""
    #adj[sommet] correspond à la listes des sommets qui ne doivant pas avoir la même couleur que lui
    nbcases = n**4
    adj = [[] for i in range(nbcases)]
    for case in range(nbcases):
        for autre_case in liste_voisins_ligne(n,case):
            adj[autre_case].append(case)
        for autre_case in liste_voisins_colonne(n,case):
            adj[autre_case].append(case)
        for autre_case in liste_voisins_bloc(n,case):
            if case not in adj[autre_case]:
                adj[autre_case].append(case)
    return adj

D'autres fonctions auxiliaires

Nous avons besoin de deux fonctions supplémentaires qui permettent de passer d’une représentation 2D d’une grille de sudoku à représentation 1D et inversement.

1. Complétez la définition de la fonction conversion_grille_vers_couleur() qui reçoit en entrée :

   • un entier n strictement positif qui représente la taille d’un sudoku (n vaut 2 ou 3) ;
   • un tableau grille à deux dimensions n² × n² qui stocke les couleurs des sommets d’un sudoku de taille n.

   def conversion_grille_vers_couleur(n, grille) :
       """permet de transformer un tableau 2D de couleurs sous la forme d'une liste 1D de couleurs (pour chaque sommet/case)"""
       nbcouleurs = n**2
       nbcases = n**4
       couleur = [0] * nbcases
       #TODO
       return couleur
   

   La fonction doit renvoyer la liste à une dimension n⁴ qui contient les mêmes valeurs que grille, écrites dans le même ordre.

   Exemple

   On passe de la grille :

   [ [3,4,1,0],
     [0,2,0,0],
     [0,0,2,0],
     [0,1,4,3] ]
   

   au tableau :

   [3, 4, 1, 0, 0, 2, 0, 0, 0, 0, 2, 0, 0, 1, 4, 3]
   

   Une réponse

   def conversion_grille_vers_couleur(n, grille) :
       """permet de transformer un tableau 2D de couleurs sous la forme d'une liste 1D de couleurs (pour chaque sommet/case)"""
       nbcouleurs = n**2
       nbcases = n**4
       couleur = [0] * nbcases
       for lig in range(nbcouleurs) :
           for col in range(nbcouleurs) :
               case = lig * nbcouleurs + col
               couleur[case] = grille[lig][col]
       return couleur
   

2. Complétez la définition de la fonction conversion_couleur_vers_grille() qui reçoit en entrée :

   • un entier n strictement positif qui représente la taille d’un sudoku (n vaut 2 ou 3) ;
   • une liste couleur à une dimension n⁴ qui stocke les couleurs des sommets d’un sudoku de taille n.

   def conversion_couleur_vers_grille(n, couleur) :
       """permet de transformer une liste de couleurs sous la forme d'un tableau de couleurs"""
       nbcouleurs = n**2
       grille = []
       #TODO
       return grille
   

   La fonction doit renvoyer la grille 2D n² × n² qui contient les mêmes valeurs que couleur, écrites dans le même ordre.

   Exemple

   On passe du tableau :

   [3, 4, 1, 0, 0, 2, 0, 0, 0, 0, 2, 0, 0, 1, 4, 3]
   

   à la grille :

   [ [3,4,1,0],
     [0,2,0,0],
     [0,0,2,0],
     [0,1,4,3] ]
   

   Une réponse

   def conversion_couleur_vers_grille(n, couleur) :
       """permet de transformer une liste de couleurs sous la forme d'un tableau de couleurs"""
       nbcouleurs = n**2
       grille = [[0] * nbcouleurs for k in range(nbcouleurs)]
       for k, c in enumerate(couleur) :
           grille[k // nbcouleurs][k % nbcouleurs] = c
       return grille
   

Vérification d'une grille de sudoku

Dans le fichier fourni, la fonction verification_grille() a été définie.

1. Écrivez les spécifications de cette fonction.

2. Rajoutez des commentaires pour expliquer les étapes de la fonction.
   En particulier, justifiez chacun des choix d’implémentation effectué.

3. Donnez la complexité de cette fonction.

Programmation Orienté Objet

Modifiez le programme et les fonctions précédentes pour qu’elles deviennent des méthodes d’une classe Sudoku dont on donne le constructeur ci-dessous :

class Sudoku :
    def __init__(self, cote_case = 3):
        self.nbcases = cote_case**4
        self.nbcouleurs = cote_case**2
        self.cote_case = cote_case
        self.adj = self.generer_graphe()