Algorithmes sur les graphes☘
Ce chapitre présente quelques algorithmes de référence sur les graphes.
Parcours en largeur☘
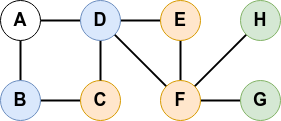
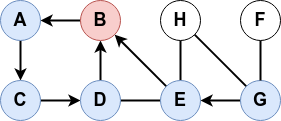
A partir d'un sommet initial, ce parcours s’effectue selon la distance (en nombre d'arêtes intermédiaires) au sommet initial (A dans l'exemple ci-dessous).
Parcours en profondeur☘
A partir d'un sommet initial, ce parcours s’effectue tant qu'il y a un voisin non exploré puis revient en arrière (backtrack).
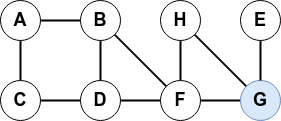
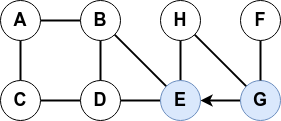
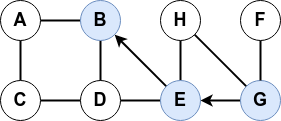
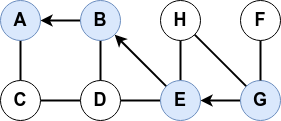
Ce parcours peut s'effectuer de manière itérative comme récursive.
- En version itérative, le « dernier » voisin est visité en premier.
- En version récursive, on visite d’abord le « premier » voisin.
Détection de cycle☘
Le parcours en profondeur permet de déterminer s’il existe un chemin dans le graphe entre deux sommets distincts. Il permet donc aussi de déterminer si le graphe comporte un cycle.
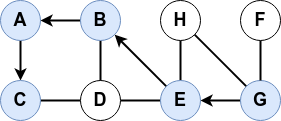
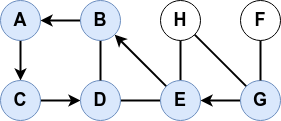
Plus court chemin☘
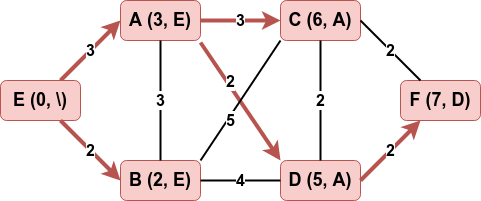
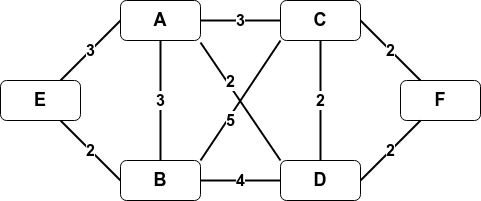
Lorsque toutes les pondérations d'un graphe pondéré sont positives, l’algorithme de Dijkstra (1959) permet d’obtenir ce plus court chemin entre un sommet initial S et chacun des sommets accessibles depuis S.
-
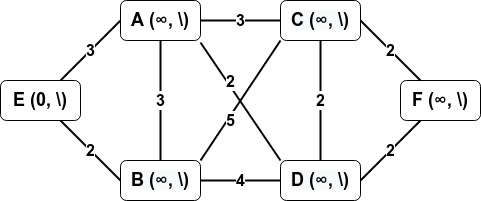
Initialisation
-
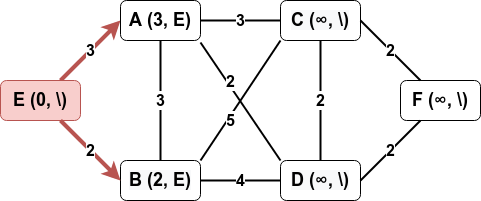
On sélectionne E et on actualise la marque de ses voisins :
-
Parmi les non visités, on visite celui qui a la marque la plus petite et on traite ses voisins non encore visités. La marque de A reste inchangée puisque qu’elle est inférieure à la somme de la marque de B avec le poids de l’arête A – B.
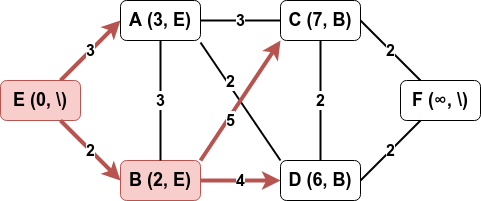
-
Parmi les non visités, on visite celui qui a la marque la plus petite et on traite ses voisins non encore visités : on modifie les marques de C et D.
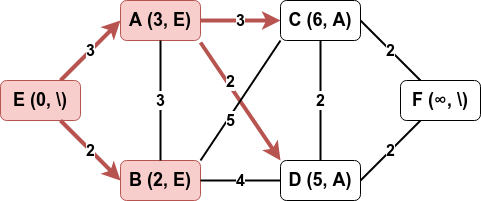
-
On continue :
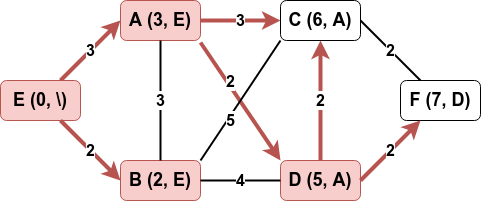
-
On continue :
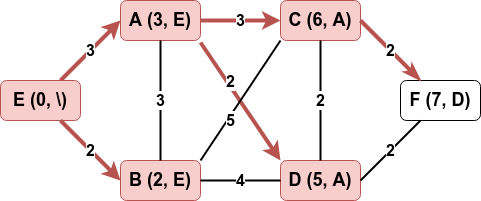
-
Dernière étape :