TP - Plus court chemin☘
Téléchargez le module TAD_GraphesPonderes.py qui
contient une implémentation orientée objet de graphe pondéré
et placez ce module dans le répertoire [E04-Algo_Graphes].
Voici l'interface de ce module :
| Méthode/Opérations | Description |
|---|---|
G = GraphePondere(dico) |
Initialisation d'un graphe pondéré sous la forme d'un dictionnaire dont
dico est initialisé à None
par défaut; |
G.est_vide() |
Renvoie True si le graphe est vide,
False sinon. |
G.sommets() |
Renvoie le tableau des sommets, sous la forme d'une liste Python. |
G.est_oriente() |
Renvoie True si le graphe est orienté,
False sinon. |
G.aretes() |
Renvoie le tableau des arêtes (des arcs si le graphe est orienté), sous la forme d'une liste Python de couples de sommets. |
G.voisins_poids(S) |
Renvoie le dictionnaire où chaque voisin ( successeur si le graphe est orienté) du sommet S passé en paramètre est associé au poids de l'arête (de l'arc) reliant ce voisin à S. |
Affichage
Pour visualiser ce graphe, la fonction print() réalise un affichage
compatible avec
l'application en ligne GraphViz.
Ce TP a pour but de vous faire programmer l'algorithme de Dijkstra
appliqué aux graphes pondérés (de poids positifs) étudié en cours.
Pour faciliter ce travail, il est conseillé d'utiliser et compléter le fichier
« à trous » : TPE04.20.py.
Partie A - Préparer les graphes de test☘
Afin de tester chacune des fonctions à programmer dans ce TP et vous
familiariser avec l'interface, programmez les deux graphes ci-dessous dans
le « main » de votre programme.
Conseils
- Dans le dictionnaire, placez les voisins (les successeurs) par ordre alphabétique.
- Affichez chaque graphe avec GraphViz afin de vérifier votre travail.
-
Graphe n°1
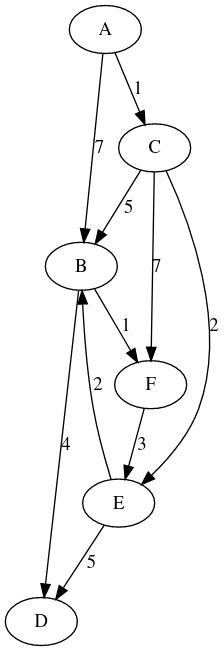
-
Graphe n°2
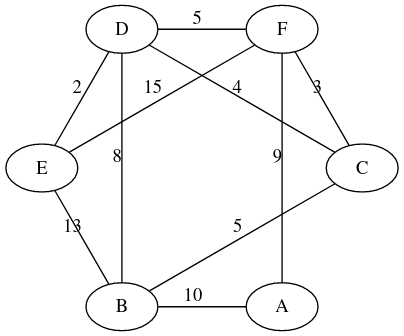
Partie B - Algorithme de Dijkstra☘
Dans cette partie, vous allez compléter, au fur et à mesure des questions,
la définition de la fonction dijkstra() qui renverra un dictionnaire associant
à chaque sommet du graphe sa distance minimale au sommet de référence passé en
paramètre.
Initialisation☘
Complétez l'initialisation des données dans la fonction dijkstra() qui
prend en paramètres un graphe et un sommet de ce graphe.
Cette initialisation va créer et (pour l'instant) renvoyer trois données :
- un dictionnaire
distancequi, à chaque sommet du graphe, associe +\infty hormis lesommetpassé en paramètre à qui est associée la valeur0; - un tableau
deja_traites, pour l'instant vide, mais qui contiendra les sommets déjà traités au cours de l'exécution de l'algorithme ; - un tableau
a_traiter, pour l'instant constitué de tous les sommets du graphe, mais qui se « videra » au cours de l'exécution de l'algorithme.
1 2 3 4 5 6 7 8 9 | |
Plan de test
>>> dijkstra(G1, 'A')
({'A': 0, 'B': inf, 'C': inf, 'D': inf, 'E': inf, 'F': inf},
[],
['A', 'B', 'C', 'D', 'E', 'F'])
>>> dijkstra(G2, 'D')
({'A': inf, 'B': inf, 'C': inf, 'D': 0, 'E': inf, 'F': inf},
[],
['A', 'B', 'C', 'D', 'E', 'F'])
Une piste
L'infini est obtenu à l'aide de l'instruction float('inf').
Sommet de plus petit poids☘
Pour mettre en oeuvre l'algorithme, il faut être en mesure d'identifier le sommet non encore sélectionné dont le « poids » (distance au sommet de référence) est le plus petit.
Pour cela, complétez la définition de la fonction sommet_poids_mini() en
respectant ses spécifiactions.
1 2 3 4 5 6 7 | |
Plan de test
>>> distance = {'A': 6, 'B': 1, 'C': 3, 'D': 2, 'E': 7, 'F': 4}
>>> a_traiter = ['A', 'C', 'E', 'F']
>>> sommet_poids_mini(a_traiter, distance)
'C'
>>> a_traiter = ['B', 'C', 'D', 'E']
>>> sommet_poids_mini(a_traiter, distance)
'B'
Mise en œuvre de l'algorithme☘
Dans le corps de la fonction dijkstra(), supprimez le renvoi du dictionnaire
distance et des tableaux deja_traites et a_traiter puis mettez en
œuvre l'algorithme suivant :
Tant qu'il reste des sommets non traités :
Sélectionner le sommet non traité de poids minimum
Pour chaque voisin (non encore traité) de ce sommet :
Si le poids du voisin est supérieur à la somme du poids du sommet et du poids de l'arête entre eux
Alors le poids du voisin est remplacé par cette somme
Marquer le sommet comme traité
Renvoyer le dictionnaire de distances
On met donc à jour le docstring de la fonction dijkstra() :
1 2 3 4 5 6 7 | |
Plan de test
>>> dijkstra(G1, 'A')
{'A': 0, 'B': 5, 'C': 1, 'D': 8, 'E': 3, 'F': 6}
>>> dijkstra(G2, 'D')
{'A': 14, 'B': 8, 'C': 4, 'D': 0, 'E': 2, 'F': 5}
Partie C - Reconstruire les chemins☘
-
Complétez la définition de la fonction
dijkstra2()qui implémente le même algorithme quedijkstra(), en renvoyant cette fois-ci un dictionnaire des prédecesseurs de chaque sommet en plus du dictionnaire des distances.
Le prédécesseur du sommet de référence seraNone.1 2 3 4 5 6 7 8
def dijkstra2(graphe, sommet): """ graphe - Graphe, graphe pondéré orienté ou non orienté sommet - Un sommet du graphe Sortie: tuple, couple de dictionnaires Le premier contenant les associations {s: distance_minimale_entre_sommet_et_s} Le second contenant les associations {s: predecesseur_de_s_dans_le_chemin_correspondant_à_cette_distance} """Plan de test
>>> dijkstra2(G1, 'A') ({'A': 0, 'B': 5, 'C': 1, 'D': 8, 'E': 3, 'F': 6}, {'A': None, 'B': 'E', 'C': 'A', 'D': 'E', 'E': 'C', 'F': 'B'}) >>> dijkstra2(G2, 'D') ({'A': 14, 'B': 8, 'C': 4, 'D': 0, 'E': 2, 'F': 5}, {'A': 'F', 'B': 'D', 'C': 'D', 'D': None, 'E': 'D', 'F': 'D'}) -
En utilisant les dictionnaires renvoyés par la fonction précédente, complétez la définition de la fonction
reconstruire_chemin()qui renvoie un arbre (sous forme de graphe pondéré ) de racine le sommet de référence et dont les branches forment les chemins les plus courts dans le graphe à partir de ce sommet.1 2 3 4 5 6 7
def reconstruire_chemin(graphe, sommet): """ graphe - Graphe, graphe pondéré orienté ou non orienté sommet - Un sommet du graphe Sortie: Graphe - graphe pondéré correspondant à l'arbre couvrant minimal obtenu en appliquant l'algorithme de Dijkstra """Test n°1
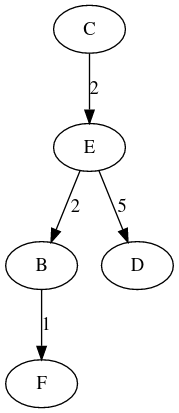
On obtient le graphe ci-dessous :>>> arbre1 = reconstruire_chemin(G1, 'A') >>> print(arbre1) digraph G { A -> C [label=1] ; B -> F [label=1] ; E -> B [label=2] ; E -> D [label=5] ; C -> E [label=2] ; }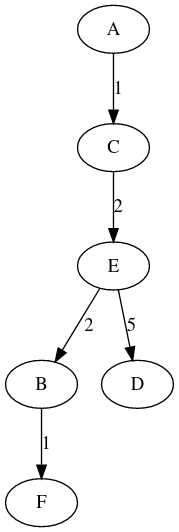
Test n°2
On obtient le graphe ci-dessous :>>> arbre2 = reconstruire_chemin(G2, 'D') >>> print(arbre2) digraph G { F -> A [label=9] ; D -> B [label=8] ; D -> C [label=4] ; D -> E [label=2] ; D -> F [label=5] ; }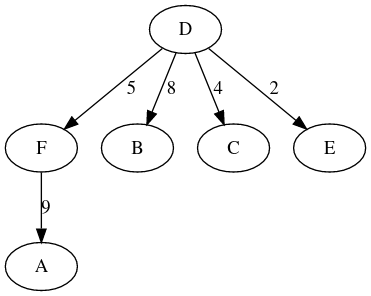
Test n°3
On obtient le graphe ci-dessous :>>> arbre3 = reconstruire_chemin(G1, 'C') >>> print(arbre3) digraph G { B -> F [label=1] ; E -> B [label=2] ; E -> D [label=5] ; C -> E [label=2] ; }