Aller au contenu

TP - Rendu de Monnaie☘

Le problème du rendu de monnaie a été étudié en 1ère. À l'époque, vous l'aviez résolu grâce à un algorithme glouton non optimal.
Ce TP a pour but de vous faire programmer une version optimale utilisant le paradigme de programmation dynamique.

Conseil

Il est conseillé de se munir des résultats du TD effectué en classe.

Téléchargez le fichier « à trous » : TPE03.20.py (clic droit -> [Enregistrer sous]) et enregistrez-le dans le répertoire [E03-Prog_Dynamique].

Présentation du problème☘

On dispose d'un tableau d'entiers distincts strictement positifs. Ce tableau, nommé pieces, est trié par ordre croissant et son premier élément vaut 1.

Exemples

On peut avoir : 

1
pieces = [1, 7, 18]

ou bien : 

1
pieces = [1, 2, 5, 10, 20, 50, 100, 200]

ou encore : 

1
pieces = [1, ...]

Ce tableau représente les différentes valeurs de pièces possibles, chacune est disponible en quantité illimité.

On dispose aussi du montant d'une somme d'argent à rendre, nommé montant.
Comment déterminer le nombre minimal de pièces nécessaires à la décomposition de ce montant ?

Vous avez vu en TD qu'une méthode dynamique pour répondre à cette question consiste à créer et compléter le contenu d'un tableau 2D nb_pieces de dimensions len(pieces) et montant + 1.

Exemple

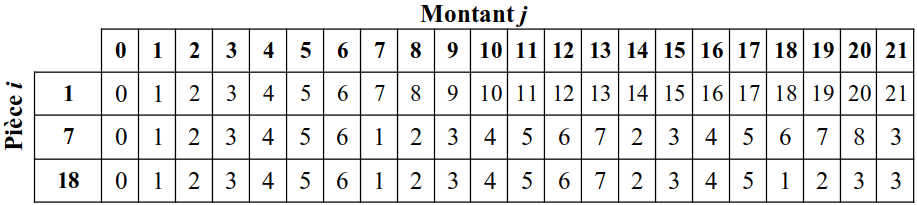
Si le montant vaut 21 et le tableau pieces est [1, 7, 18], alors on peut construire le tableau : Tableau

D'après ce tableau, le montant 21 nécessite 3 pièces de notre système monétaire : 3 pièces de valeur 7.

La relation de récurrence permettant de construire le tableau nb_pieces est :

nb_{pieces}(i, j) = \left\{ \begin{array}{ll} nb_{pieces}(i-1, j) & si \; pieces[i] > j \\ min(nb_{pieces}(i-1, j), 1 + nb_{pieces}(i, j-pieces[i]) & sinon \\ \end{array} \right.

Partie 1 - Programmation itérative « Bottom-Up »☘

  1. Complétez la définition de la fonction creer_tab_nb_pieces() qui doit renvoyer le tableau 2D présenté dans la partie précédente.

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
    def creer_tab_nb_pieces(montant, pieces):
    """
    montant - int, entier positif ou nul
    pieces - list, tableau d'entiers positifs distincts, triés par ordre croissant
                   Le plus petit entier DOIT avoir pour valeur 1
    Sortie: list - Tableau de len(pieces) tableaux ayant chacun montant+1 éléments
            La case de coordonnées [i][j] contient le nombre minimal de pièces
            nécessaires pour décomposer le montant j avec des valeurs de pièces
            prises dans le sous-tableau pieces[0..i]
            Version itérative "Bottom-Up"
    >>> pieces = [1, 7, 18]
    >>> creer_tab_nb_pieces(21, pieces)
    [[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21], [0, 1, 2, 3, 4, 5, 6, 1, 2, 3, 4, 5, 6, 7, 2, 3, 4, 5, 6, 7, 8, 3], [0, 1, 2, 3, 4, 5, 6, 1, 2, 3, 4, 5, 6, 7, 2, 3, 4, 5, 1, 2, 3, 3]]
    """
    Des pistes

    1. Commencez par initialiser un tableau dont toutes les cases contiennent la même valeur. Celle-ci ne doit pas être un nombre de pièces possible pour la décomposition de montant.

    2. Quelle pièce renvoie la décomposition la plus grande en nombre de pièces ? Quelle décomposition est alors la plus grande ?
      Augmentez-la un peu et vous pourrez initialiser le tableau.

    3. Complétez la première ligne et la première colonne.

    4. Utilisez la relation de récurrence pour compléter les autres cases du tableau.

  2. Pour mieux visaliser le tableau obtenu, complétez la définition de la fonction affiche_tab_2D().
    Utilisez le test ci-dessous pour adapter cet affichage.

    Test d'affichage

    >>> affiche_tab_2D([[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]])
1   2   3   
4   5   6   
7   8   9   
10  11  12

  3. Utilisez les deux fonctions précédentes pour tester votre travail.

    Exemple de test

    >>> tab = creer_tab_nb_pieces(21, [1, 2, 5, 10, 20, 50])
>>> affiche_tab_2D(tab)
0   1   2   3   4   5   6   7   8   9   10  11  12  13  14  15  16  17  18  19  20  21  
0   1   1   2   2   3   3   4   4   5   5   6   6   7   7   8   8   9   9   10  10  11  
0   1   1   2   2   1   2   2   3   3   2   3   3   4   4   3   4   4   5   5   4   5   
0   1   1   2   2   1   2   2   3   3   1   2   2   3   3   2   3   3   4   4   2   3   
0   1   1   2   2   1   2   2   3   3   1   2   2   3   3   2   3   3   4   4   1   2   
0   1   1   2   2   1   2   2   3   3   1   2   2   3   3   2   3   3   4   4   1   2

  4. Complétez la définition de la fonction decomposition_mini() qui doit renvoyer la plus petite décomposition de montant obtenue à partir du système monétaire donné par le tableau pieces.

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
    def decomposition_mini(montant, pieces):
    """
    montant - int, entier positif ou nul
    pieces - list, tableau d'entiers positifs distincts, triés par ordre croissant
                   Le plus petit entier DOIT avoir pour valeur 1
    Sortie: list - Tableau des valeurs de la décomposition de montant utilisant
                    le minimum de pièces

    >>> pieces = [1, 7, 18]
    >>> decomposition_mini(21, pieces)
    [7, 7, 7]
    """
    Des pistes

    1. Parcourez le tableau créé en question 1. à partir de la dernière case puis « remontez » dans ce tableau en suivant la décomposition minimale.

    2. Distinguez une décomposition identique avec un montant de pièce plus petit.

    3. Sinon, effectuez un « décalage » sur la même ligne de pièce.

    Exemple de test

    >>> pieces = [1, 2, 5, 10, 20, 50]
>>> decomposition_mini(21, pieces)
[20, 1]

Partie 2 - Programmation récursive « Top-Down »☘

  1. Complétez la définition de la fonction creer_tab_nb_pieces_rec() qui doit renvoyer le tableau 2D présenté dans la partie précédente, avec un tableau complété récursivement.

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
    def creer_tab_nb_pieces_rec(montant, pieces):
    """
    montant - int, entier positif ou nul
    pieces - list, tableau d'entiers positifs distincts, triés par ordre croissant
                   Le plus petit entier DOIT avoir pour valeur 1
    Sortie: list - Tableau de len(pieces) tableaux ayant chacun montant+1 éléments
            La case de coordonnées [i][j] contient le nombre minimal de pièces
            nécessaires pour décomposer le montant j avec des valeurs de pièces
            prises dans le sous-tableau pieces[0..i]
            Version récursive "Top-Down"

    >>> pieces = [1, 7, 18]
    >>> creer_tab_nb_pieces_rec(21, pieces)
    [[0, 22, 22, 3, 22, 22, 22, 7, 22, 22, 22, 22, 22, 22, 14, 22, 22, 22, 22, 22, 22, 21], [0, 22, 22, 3, 22, 22, 22, 1, 22, 22, 22, 22, 22, 22, 2, 22, 22, 22, 22, 22, 22, 3], [22, 22, 22, 3, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 3]]
    """

    Exemple de test

    >>> pieces = [1, 2, 5, 10, 20, 50]
>>> tab = creer_tab_nb_pieces_rec(21, pieces)
>>> affiche_tab_2D(tab)
0   1   2   3   4   5   6   7   8   9   10  11  12  13  14  15  16  17  22  19  22  21  
0   1   1   2   2   3   3   4   4   5   5   6   6   7   7   8   8   9   22  10  22  11  
22  1   22  22  22  22  2   22  22  22  22  3   22  22  22  22  4   22  22  22  22  5   
22  1   22  22  22  22  22  22  22  22  22  2   22  22  22  22  22  22  22  22  22  3   
22  1   22  22  22  22  22  22  22  22  22  22  22  22  22  22  22  22  22  22  22  2   
22  22  22  22  22  22  22  22  22  22  22  22  22  22  22  22  22  22  22  22  22  2

  2. Expliquez à l'enseignant pourquoi autant de cases contiennent la valeur 22.

  3. Est-ce gênant pour la recherche de la décomposition ?
    Testez-le en adaptant la fonction decomposition_mini() pour qu'elle fasse appel au tableau renvoyé par la fonction creer_tab_nb_pieces_rec().