Relation de récurrence

Vocabulaire

Dans cette page, on assimile un pixel à ses coordonnées dans l'image.
En d'autres termes, l'expression « le pixel (x, y) » signifie en fait « le pixel de coordonnées (x, y) ».

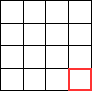
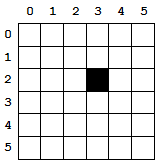
Afin de visualiser les pixels, on va représenter l'image dans un quadrillage. Ainsi, dans l'image ci-dessous, seul le pixel (3, 2) est noir.

Partie 1 - Parcours de l'image

On a vu, au cours des pages précédentes, comment parcourir les pixels de l'image, de gauche à droite et de haut en bas :

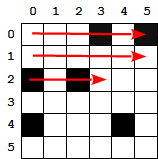
Chaque nouveau pixel exploré peut donc tirer parti des pixels déjà explorés. Pour comprendre comment, on va associer un tableau à cette image. Pour chaque nouveau pixel, on écrira dans ce tableau :

• 0 si le pixel est noir,
• 1 s'il est blanc et permet de réaliser un carré blanc de côté 1 pixel (donc lui-même),
• 2 s'il permet de réaliser un carré de côté 2 pixels,
• etc...

Un exemple de parcours

Vous allez rechercher le (ou les) plus grands carrés blancs dans l'image suivante :

1. Les pixels de la première ligne ont comme seule information leur voisin de gauche (sauf le premier de la ligne). Cependant deux pixels côte à côte ne permettent pas de constituer un carré de côté 2. La première ligne ne peut donc contenir que des « 0 » ou des « 1 ».
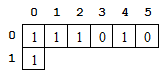
   Sur votre cahier, recopiez et remplissez la première ligne du tableau suivant les règles définies dans le paragraphe « Parcours de l'image » :
   

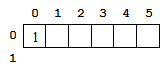
   Une réponse

   

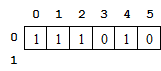
2. On passe à la deuxième ligne. Le pixel (0, 1) de la colonne de gauche ne connaît que son voisin du dessus. A eux deux, ils ne peuvent pas constituer un carré blanc.
   Complétez votre tableau avec la valeur à placer dans la case en ligne 1 et colonne 0.

   Une réponse

   

3. On passe au pixel (1, 1) :
   
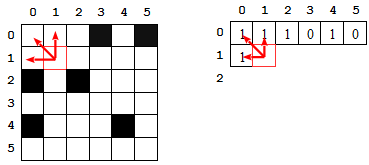
   Ce pixel « connaît » suffisamment de voisins pour déterminer si, à eux quatre, ils forment un carré blanc de taille 2. Dans ce cas, il semble intéressant d'écrire « 2 » plutôt que « 1 » dans la case correspondante du tableau. Cela permettra d'indiquer que ce pixel est le coin bas-droite d'un carré blanc de taille 2.
   Justifiez les valeurs de la ligne n°1 du tableau :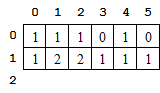

   Une réponse

   • Comme indiqué dans l'énoncé, le pixel (1, 1) est le coin bas-droit d'un carré blanc de taille 2. On écrit donc « 2 » dans la case correspondante du tableau.
   • Le pixel (2, 1) est le coin bas-droit d'un carré blanc de taille 2. On écrit donc « 2 » dans la case correspondante du tableau.
   • Le pixel (3, 1) est « surmonté » d'un pixel noir. Même si (3, 1) est blanc, il ne peut pas être le coin bas-droit d'un carré blanc de taille 2. On écrit donc « 1 » dans la case correspondante du tableau.
   • Le pixel (4, 1) est blanc et a pour voisin haut-gauche un pixel noir. Même si (4, 0) et (3, 1) sont blancs, (4, 1) ne peut pas être le coin bas-droit d'un carré blanc de taille 2. On écrit donc « 1 » dans la case correspondante du tableau.
   • Par un raisonnement analogue, le pixel (5, 1) ne peut pas être le coin bas-droit d'un carré blanc de taille 2. On écrit donc « 1 » dans la case correspondante du tableau.

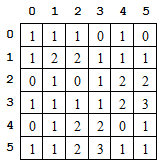
4. Complétez à présent entièrement les cases du tableau en identifiant éventuellement les carrés de taille supérieure à 2.

   Une réponse

   

Partie 2 - Étude du tableau associé à l'image

Dans cette partie, on s'intéresse au tableau de représentation des pixels.

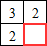
1. La case bas-droite entourée en rouge ci-contre correspond à un pixel blanc dans l'image. Quelle valeur faut-il placer dans cette case ?
   Dessinez une image contenant des pixels noirs et blancs et qui peut être associée à ces quatre cases.

   Réponse du 1.

   Les plus petits carrés blancs autour du pixel considéré sont de taille 2 donc, en associant le pixel bas-droit supplémentaire, on forme un carré blanc de taille 3.

   Le tableau :

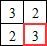
   Un exemple d'image associée :

   

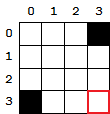
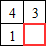
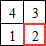
2. La case bas-droite entourée en rouge ci-contre correspond à un pixel blanc dans l'image. Quelle valeur faut-il placer dans cette case ?
   Dessinez une image contenant des pixels noirs et blancs et qui peut être associée à ces quatre cases.

   Réponse du 2.

   Les plus petits carrés blancs autour du pixel considéré sont de taille 1 donc, en associant le pixel bas-droit supplémentaire, on forme un carré blanc de taille 2.

   Le tableau :

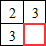
   Un exemple d'image associée (les quatre cases du tableau ne nous donnent pas assez d'information pour déterminer la couleur des pixels identifiés par des points d'interrogation) :

   

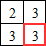
3. La case bas-droite entourée en rouge ci-contre correspond à un pixel blanc dans l'image. Quelle valeur faut-il placer dans cette case ?
   Dessinez une image contenant des pixels noirs et blancs et qui peut être associée à ces quatre cases.

   Réponse du 3.

   Les plus petits carrés blancs autour du pixel considéré sont de taille 2 donc, en associant le pixel bas-droit supplémentaire, on forme un carré blanc de taille 3.

   Le tableau :

   Un exemple d'image associée :

   

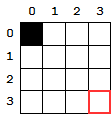
4. On considère le pixel représenté par la case bas-droite entourée en rouge ci-contre.

   1. À quelle(s) condition(s) cette case contiendra-t-elle la valeur 2 ?
   2. À quelle(s) condition(s) cette case contiendra-t-elle la valeur 3 ?
   3. Soit $n$ un entier strictement positif.
      À quelle(s) condition(s) cette case contiendra-t-elle la valeur $n$ ?
   Réponses du 4.

   a. Pour que la case bas-droite contienne un « 2 », il faut :
   - qu'elle corresponde à un pixel blanc dans l'image,
   - qu'au moins une des cases au-dessus, à gauche et haut-gauche contienne un « 1 ».
   Elles peuvent toutes contenir « 1 », mais ce n'est pas obligatoire : un seul suffit.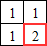

   b. Pour que la case bas-droite contienne un « 3 », il faut :
   - qu'elle corresponde à un pixel blanc dans l'image,
   - qu'au moins une des cases au-dessus, à gauche et haut-gauche contienne un « 2 ».
   Elles peuvent toutes contenir « 2 », mais ce n'est pas obligatoire : un seul suffit.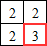

   c. Pour que la case bas-droite contienne un « n », il faut :
   - qu'elle corresponde à un pixel blanc dans l'image,
   - qu'au moins une des cases au-dessus, à gauche et haut-gauche contienne un « n-1 ».
   Elles peuvent toutes contenir « n-1 », mais ce n'est pas obligatoire : un seul suffit.
   

5. Voici le tableau d'association complet pour une image noir et blanc de dimensions $10 \times 10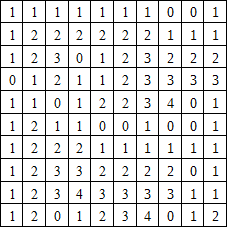$ : En utilisant les informations données par ce tableau, dessinez l'image correspondante sur votre cahier.

   Réponses du 5.

   Il suffit de remplacer chaque « 0 » par un pixel noir...

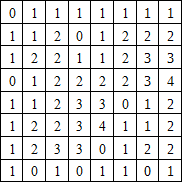
6. Réalisez sur votre cahier le tableau de correspondance de l'image suivante :

   Réponse du 6.

   

Partie 3 - Généralisation

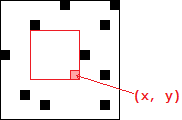
Les observations précédentes permettent de modifier légèrement la problématique initiale :

Déterminer la taille du plus grand carré blanc dont le pixel en bas à droite a pour coordonnées (x, y).

1. On souhaite savoir si, dans l'image, un carré de côté $n$ pixels est blanc.
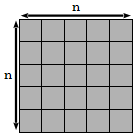   A l'aide du travail déjà réalisé, donnez les conditions (en fonction de $n$) qu'il faut vérifier pour que ce carré soit effectivement blanc puis prouvez ces conditions à l'aide de dessins. Pour cela, on pourra s'intéresser aux carrés voisins de taille $(n-1)$.

   Réponse

   Un carré de côté $n$ pixels est blanc si et seulement si :

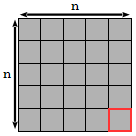
   • Le pixel en bas à droite de ce carré est blanc :

   • Les trois carrés de côté $(n-1)$ pixels en bas à gauche, en haut à gauche et en haut à droite sont blancs :

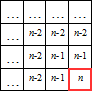
   Cela correspond au tableau de représentation obtenu en fin de question 4. dans la partie précédente :

2. Dans le tableau de tableau de représentation des pixels, on a la configuration suivante :

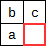
   a. Que représentent les nombres a, b et c dans ce tableau ?
   b. On admet que la case bas-droite entourée en rouge correspond à un pixel blanc dans l'image.
   Quelle valeur faut-il placer dans cette case ?

   Conclusion

   • Le nombre a signifie que le pixel correspondant dans l'image est le pixel bas-droit d'un carré blanc de côté a pixels.

   • Le nombre b signifie que le pixel correspondant dans l'image est le pixel bas-droit d'un carré blanc de côté b pixels.

   • Le nombre c signifie que le pixel correspondant dans l'image est le pixel bas-droit d'un carré blanc de côté c pixels.

   • Dans la case entourée en rouge, il faut placer la valeur 1 + min(a, b, c) car ce pixel blanc permet d'agrandir de 1 le côté du carré blanc formé à partir du plus petit des trois carrés blancs qui l'entourent.