Exercices d'entraînement

Ces exercices doivent être utilisés pour vous entraîner à programmer. Ils sont généralement accompagnés d'aide et de leur solution pour vous permettre de progresser.

Avant de vous précipiter sur ces solutions dès la première difficulté, n'oubliez pas les conseils suivants :

• Avez-vous bien fait un schéma au brouillon pour visualiser le problème posé ?
• Avez-vous essayé de rédiger un algorithme en français, avec vos propres mots, avant de vous lancer dans la programmation sur machine ?
• Avez-vous utilisé des affichages intermédiaires, des print(), pour visualiser au fur et à mesure le contenu des variables ?
• Avez-vous testé le programme avec les propositions de tests donnés dans l'exercice ?
• Avez-vous testé le programme avec de nouveaux tests, différents de ceux proposés ?

Rappels

• Chaque programme Python doit être sauvegardé sous forme de fichier texte avec l'extension .py.
  Enregistrez ce fichier dans le dossier [E03-Prog_Dynamique] avec le nom donné à l'exercice : ProgE03.51.py, ProgE03.52.py, etc...
• Pour exécuter ce programme, il suffit de le sauvegarder puis d'appuyer sur la touche [F5].
• Le programme principal doit contenir un appel au module doctest :

  ##----- Programme principal et tests -----##
  if __name__ == '__main__':
      import doctest
      doctest.testmod()
  

ProgE03.51 - Sous tableau maximum

Étant donné un tableau tab de n nombres entiers (positifs ou négatifs), on cherche la plus grande somme d'éléments contigus du tableau, c'est-à-dire la plus grande somme de sous-tableaux tab[i..j] avec i $\leqslant$ j.

Exemples

1. Soit tab = [4, -6, 7, -1, 8, -50, 3].
   La plus grande somme trouvée dans ce tableau est 14, elle est obtenue avec le sous-tableau tab[2..4] = [7, -1, 8].

2. Pour tab = [-2, -3, -4], la plus grande somme est -2.

Complément

Les fonctions min() et max() de Python sont autorisées dans cet exercice.

1. Copiez/collez et complétez le corps de la fonction itérative somme_max() à l'aide de la relation de récurrence étudiée en TD.

   def somme_max(tab):
       """
       tab - list, tableau d'entiers naturels
       Sortie: int - Plus grande somme des sous-tableaux d'éléments contigus de tab
       >>> somme_max([4 , -6 , 7 , -1 , 8 , -50 , 3])
       14
       >>> somme_max([-2, -3, -4])
       -2
       """ 
   

   Une solution

   def somme_max(tab):
       """
       tab - list, tableau d'entiers naturels
       Sortie: int - Plus grande somme des sous-tableaux d'éléments contigus de tab
       >>> somme_max([4 , -6 , 7 , -1 , 8 , -50 , 3])
       14
       >>> somme_max([-2, -3, -4])
       -2
       """ 
       n = len(tab)
   
       M = [0] * n
       M[0] = tab[0] 
   
       for j in range(1, n):
           M[j] = max(tab[j], M[j-1] + tab[j])
   
       return max(M)
   

2. Copiez/collez et complétez le corps de la fonction itérative sous_tab_max() qui renvoie le sous-tableau maximum du tableau tab passé en paramètre.

   def sous_tab_max(tab):
       """
       tab - list, tableau d'entiers naturels
       Sortie: list - Sous-tableau de tab ayant la plus grande somme d'éléments contigus
       >>> sous_tab_max([4 , -6 , 7 , -1 , 8 , -50 , 3])
       [7, -1, 8]
       >>> sous_tab_max([-2, -3, -4])
       [-2]
       """ 
   

   Une solution

   def sous_tab_max(tab):
       """
       tab - list, tableau d'entiers naturels
       Sortie: list - Sous-tableau de tab ayant la plus grande somme d'éléments contigus
       >>> sous_tab_max([4 , -6 , 7 , -1 , 8 , -50 , 3])
       [7, -1, 8]
       >>> sous_tab_max([-2, -3, -4])
       [-2]
       """ 
       n = len(tab)
   
       M = [0] * n
       M[0] = tab[0] 
   
       for j in range(1, n):
           M[j] = max(tab[j], M[j-1] + tab[j])
   
       indice_max = 0
       for i in range(1, n):
           if M[i] > M[indice_max]:
               indice_max = i
   
       i = indice_max
       sous_tab = [tab[i]]
       somme = tab[i]
       while somme != M[indice_max]:
           i = i-1
           somme += tab[i]
           sous_tab = [tab[i]] + sous_tab
       return sous_tab
   

3. Copiez/collez et complétez le corps de la fonction somme_max_rec() qui renvoie la plus grande somme des sous-tableaux d'éléments contigus de tab à l'aide d'une programmation « Top-Down », c'est-à-dire en faisant appel à une fonction récursive auxiliaire.

   def somme_max_rec(tab):
       """
       tab - list, tableau d'entiers naturels
       Sortie: int - Plus grande somme des sous-tableaux d'éléments contigus de tab
       >>> somme_max_rec([4 , -6 , 7 , -1 , 8 , -50 , 3])
       14
       >>> somme_max_rec([-2, -3, -4])
       -2
       """ 
   

   Une solution avec une sous-fonction récursive

   def somme_max_rec(tab):
       """
       tab - list, tableau d'entiers naturels
       Sortie: int - Plus grande somme des sous-tableaux d'éléments contigus de tab
       >>> somme_max_rec([4 , -6 , 7 , -1 , 8 , -50 , 3])
       14
       >>> somme_max_rec([-2, -3, -4])
       -2
       """ 
       n = len(tab)
       M = [None] * n
       M[0] = tab[0] 
   
       def calcul(i):
           if M[i] is None:
               M[i] = tab[i] + max(0, calcul(i-1))
           return M[i]
   
       calcul(n-1)
       return max(M)
   

   Une solution avec une fonction auxiliaire récursive

   def calcul_sommes(memo, tab, i):
       if memo[i] is None:
           memo[i] = tab[i] + max(0, calcul_sommes(memo, tab, i-1))
       return memo[i]
   
   def somme_max_rec2(tab):
       """
       tab - list, tableau d'entiers naturels
       Sortie: int - Plus grande somme des sous-tableaux d'éléments contigus de tab
       >>> somme_max_rec2([4 , -6 , 7 , -1 , 8 , -50 , 3])
       14
       >>> somme_max_rec2([-2, -3, -4])
       -2
       """ 
       n = len(tab)
       M = [None] * n
       M[0] = tab[0] 
   
       calcul_sommes(M, tab, n-1)
       return max(M)
   

ProgE03.52 - Coefficients binomiaux

Une expérience aléatoire comportant deux issues (succès et échec) est répétée $n$ fois de manière identique et indépendante. On peut représenter cette répétition par un arbre binaire :

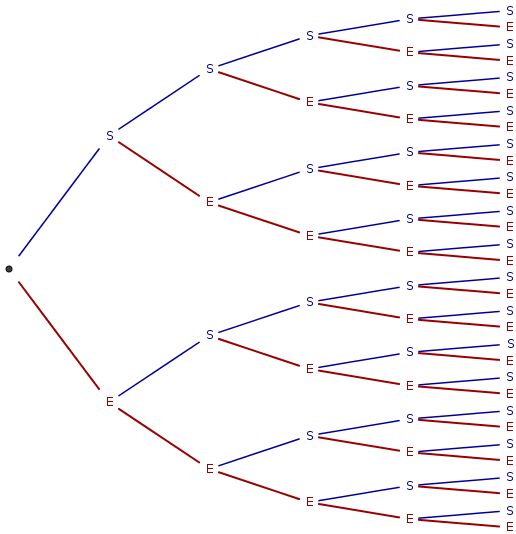
On appelle coefficient binomial $\begin{pmatrix} n\\ p \end{pmatrix}$ (se lit « $p$ parmi $n$) le nombre de chemins avec $p$ succès dans l'arbre précédent. Par exemple, le coefficient $\begin{pmatrix} 5\\ 2 \end{pmatrix}$ vaut 10 :

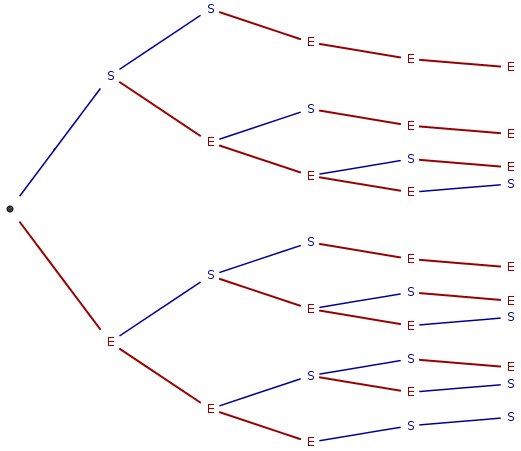
Le triangle de Pascal permet d'obtenir ces coefficients à l'aide de la relation de récurrence suivante : pour tout entier naturel $p$ tel que $0 \leq p \leq n$, on a $\begin{pmatrix} n\\ 0 \end{pmatrix} = \begin{pmatrix} n\\ n \end{pmatrix} = 1$ et $\begin{pmatrix} n\\ p \end{pmatrix} = \begin{pmatrix} n-1\\ p \end{pmatrix} + \begin{pmatrix} n-1\\ p-1 \end{pmatrix}$.

Cette relation permet d'établir le tableau ci-dessous :

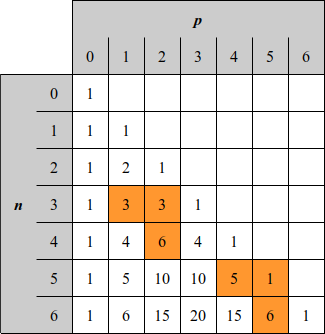
Le but de cet exercice est de programmer le calcul du coefficient $\begin{pmatrix} n\\ p \end{pmatrix}$, en utilisant le paradigme de programmation dynamique. Pour cela, vous utiliserez un dictionnaire permettant de conserver les résultats déjà calculés dans un dictionnaire dont les clés sont les couples $(p, n)$.

Copiez, collez et complétez la définition de la fonction coeff_bin() en suivant ce principe.

def coeff_bin(p, n):
    """
    p, n - int, entiers strictement positifs tels que 0 <= p <= n
    Sortie: int - Coefficient binomial "p parmi n"
    >>> coeff_bin(1, 3)
    3
    >>> coeff_bin(4, 6)
    15
    >>> coeff_bin(5, 14)
    2002
    """ 

Attention, l'appel ci-dessous doit renvoyer une erreur :

>>> coeff_bin(5, 3)
AssertionError: index out of range

Une solution « récursive » en programmation Top-Down

def coeff_bin(p, n):
    """
    p, n - int, entiers strictement positifs tels que 0 <= p <= n
    Sortie: int - Coefficient binomial "p parmi n"
    >>> coeff_bin(1, 3)
    3
    >>> coeff_bin(4, 6)
    15
    >>> coeff_bin(5, 14)
    2002
    """
    assert 0 <= p <= n, "index out of range"
    dico = {(0, i):1 for i in range(n+1)}
    for i in range(n+1):
        dico[(i, i)]=1

    def pascal(p, n):
        if (p, n) not in dico.keys():
            dico[(p, n)] = pascal(p, n-1) + pascal(p-1, n-1)
        return dico[(p, n)]

    return pascal(p, n)

Une solution « itérative » en programmation Bottom-Up

def coeff_bin_bis(p, n):
    """
    p, n - int, entiers strictement positifs tels que 0 <= p <= n
    Sortie: int - Coefficient binomial "p parmi n"
    >>> coeff_bin_bis(1, 3)
    3
    >>> coeff_bin_bis(4, 6)
    15
    >>> coeff_bin_bis(5, 14)
    2002
    """
    assert 0 <= p <= n, "index out of range"
    dico = {(0, i):1 for i in range(n+1)}
    for i in range(n+1):
        dico[(i, i)]=1

    for i in range(2, n+1):
        for j in range(1, i):
            dico[(j, i)] = dico[(j, i-1)] + dico[(j-1, i-1)]

    return dico[(p, n)]

ProgE03.53 - Découper une pizza

Important

Pas de solutions dans cet exercice. Essayez de trouver seul.
À ce stade de l'année, vous en êtes capable !

Une ville réalise chaque année un défi pour obtenir le record de la plus grande pizza du monde. Une fois la pizza réalisée, celle-ci est vendue a des tarifs différents selon la taille des parts. Ces tarifs sont imposés par la ville mais chacun des participants pour préparer les parts qu’il souhaite.

Les services de la ville proposent les tarifs suivants pour des parts allant jusqu’à 10 mètres :

Taille i de la part	0	1	2	3	4	5	6	7	8	9	10
Prix de vente pi	0	2	4	5	6	8	9	11	12	13	14

Un participant souhaite pré-découper des parts dans son morceau de pizza afin d’en retirer le bénéfice maximum.

Exemples

1. Avec un morceau mesurant 3 mètres, le découpage apportant le plus grand bénéfice correspond à trois parts de 1 mètre.

2. Avec un morceau mesurant 5 mètres, le découpage apportant le plus grand bénéfice correspond à deux parts de 2 mètres et une part de 1 mètre.

Complément

Les fonctions min() et max() de Python sont autorisées dans cet exercice.

1. Copiez/collez et complétez le corps de la fonction impérative benef_maximal() à l'aide de la relation de récurrence étudiée en TD.

   def benef_maximal(n, prix):
       """
       n - int, longueur (en mètre) du morceau initial à partager
       prix - list, tableau des prix proposés par la ville
                    Les indices correspondent à la taille de la part découpée
       Sortie: int - Bénéfice maximal obtenu pour un découpage en parts
               de taille entière du morceau initial de taille n
               Version impérative "Bottom-Up"
       >>> benef_maximal(4, [0, 2, 6, 8, 9])
       12
       >>> benef_max_rec(4, [0, 1, 5, 8, 9, 10])
       10
       """
   

   tests supplémentaires

   Vous pouvez utiliser la liste de prix ci-dessous pour effectuer vos tests, ou bien inventer votre propore liste.

   prix = [0, 1, 2, 4, 5, 6, 8, 9, 10, 12, 13]
   

2. Copiez/collez et complétez le corps de la fonction itérative decoupage_optimal() qui reprend le principe de la fonction précédente et l'améliore en renvoyant, en plus du bénéfice optimal, la liste des découpes à réaliser dans le morceau de pizza pour obtenir ce bénéfice.

   def decoupage_optimal(n, prix):
       """
       n - int, longueur (en mètre) du morceau initial à partager
       prix - list, tableau des prix proposés par la ville
                    Les indices correspondent à la taille de la part découpée
       Sortie: tuple - couple constitué du :
                       - Bénéfice maximal obtenu pour un découpage en parts
                           de taille entière du morceau initial de taille n
                       - tableau des découpages à réaliser
       >>> decoupage_optimal(4, [0, 2, 6, 8, 9])
       (12, [2, 2])
       >>> decoupage_optimal(4, [0, 1, 5, 8, 9, 10])
       (10, [2, 2])
       """
   

   Une piste

   Mémorisez aussi les découpages en utilisant un tableau de supplémentaire de mémorisation.

3. Copiez/collez et complétez le corps de la fonction benef_max_rec() qui renvoie le plus grand bénéfice obtenu pour la découpe d'un morceau de taille n à l'aide d'une programmation « Top-Down », c'est-à-dire en faisant appel à une fonction récursive auxiliaire.

   def benef_max_rec(n, prix):
       """
       n - int, longueur (en mètre) du morceau initial à partager
       prix - list, tableau des prix proposés par la ville
                    Les indices correspondent à la taille de la part découpée
       Sortie: int - Bénéfice maximal obtenu pour un découpage en parts
               de taille entière du morceau initial de taille n
               Version récursive "Top-Down"
       >>> benef_max_rec(4, [0, 2, 6, 8, 9])
       12
       >>> benef_max_rec(4, [0, 1, 5, 8, 9, 10])
       10
       """
   

   Attention

   Seul le bénéfice nous intéresse ici, le résultat à obtenir est le même qu'en question 1.