Programmation dynamique récursive☘
Question n°1☘
On considère l'image ci-contre  de dimension 12×12 dont voici une version agrandie :
de dimension 12×12 dont voici une version agrandie :

- Téléchargez cette image et sauvegardez-la dans votre dossier personnel.
-
Téléchargez le programme suivant.
Que pouvez-vous dire de la fonctionpgcb_rec()?Le code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55
from PIL import Image def pgcb_rec(source, x, y): """ source - référence d'une image carrée (au format 'L') déjà importée à l'aide de PIL au format 'L' La "couleur" d'un pixel noir est 0, celle d'un pixel blanc est 255 x, y - coordonnées entières du pixel en cours d'étude Sortie: valeur de memo[y][x] """ couleur = source.getpixel( (x, y) ) if couleur == 0: return 0 elif x==0 or y==0: return 1 else: return 1 + min(pgcb_rec(source, x-1, y), pgcb_rec(source, x-1, y-1), pgcb_rec(source, x, y-1)) def recherche_pgcb_rec(source): """ source - référence d'une image carrée (au format 'L') déjà importée à l'aide de PIL au format 'L' La "couleur" d'un pixel noir est 0, celle d'un pixel blanc est 255 Sortie: tuple - taille du côté du (ou des) plus grand(s) carré(s) blanc(s) de cette image et liste des coordonnées des coins haut/gauche de ceux-ci """ largeur, hauteur = source.size # Création du tableau d'association memo = [[0 for i in range(largeur)] for j in range(hauteur)] # On complète récursivement le tableau d'association for x in range(largeur): for y in range(hauteur): memo[y][x] = pgcb_rec(source, x, y) print(memo[y][x]) for ligne in memo: print(ligne) # On parcourt ce tableau pour déterminer les PGCB taille_max = 0 liste_coor = [] for x in range(largeur): for y in range(hauteur): if (taille_max != 0) and memo[x][y] == taille_max: liste_coor.append((y, x)) # Transposition elif memo[x][y] > taille_max: taille_max = memo[x][y] liste_coor = [(y, x)] # Transposition liste_coor = [(coor[0]-taille_max+1, coor[1]-taille_max+1) for coor in liste_coor] return (taille_max, liste_coor) ##----- Programe principal -----## source = Image.open('Ex_00_Image_12x12.png') result = recherche_pgcb_rec(source) print(result)Réponse du 2.
La fonction
pgcb_rec()est récursive, elle implémente exactement la relation de récurrence déterminée auparavant :- Si le pixel
(x, y)est noir, alors
memo[y][x] = 0. - Si
(x, y)est blanc et qu'il appartient à la première ligne (en haut) ou la première colonne (à gauche), alors
memo[y][x] = 1. - Si
(x, y)est blanc et qu'il n'est pas dans le cas précédent, alors
memo[y][x] = 1 + min(memo[y][x-1], memo[y-1][x-1], memo[y-1][x]).
- Si le pixel
-
Exécutez ce code.
-
Ce programme est-il efficace, c'est-à-dire détermine-t-il correctement la taille et les positions des plus grands carrés blancs de l'image ?
Réponse du 3. a.
Ce programme est efficace. Pour l'image donné en exemple, il renvoie le même tuple que les algorithmes étudiés jusqu'à présent, hormis l'algorithme glouton (qui lui, n'est pas efficace).
(5, [(7, 0), (7, 1)]) -
Ce programme est-il rapide ? Justifiez (vous pouvez faire des dessins pour cela)
Réponse du 3. b.
Ce programme devient très vite très lent. En effet, la pile d'appels récursifs devient vite très importante.
Voici un exemple des appels réalisés pour un carré blanc de taille 3×3.
- Le pixel entouré de rouge est celui sur lequel la fonction
pgcb_rec()est appelé. - Le carré entouré de bleu correspond aux appels récursifs qui seront effectués ensuite.
- Le pixel colorié en vert est un pixel de la première ligne ou de la première colonne. On peut déterminer sa valeur donc les appels récursifs s'arrêtent.
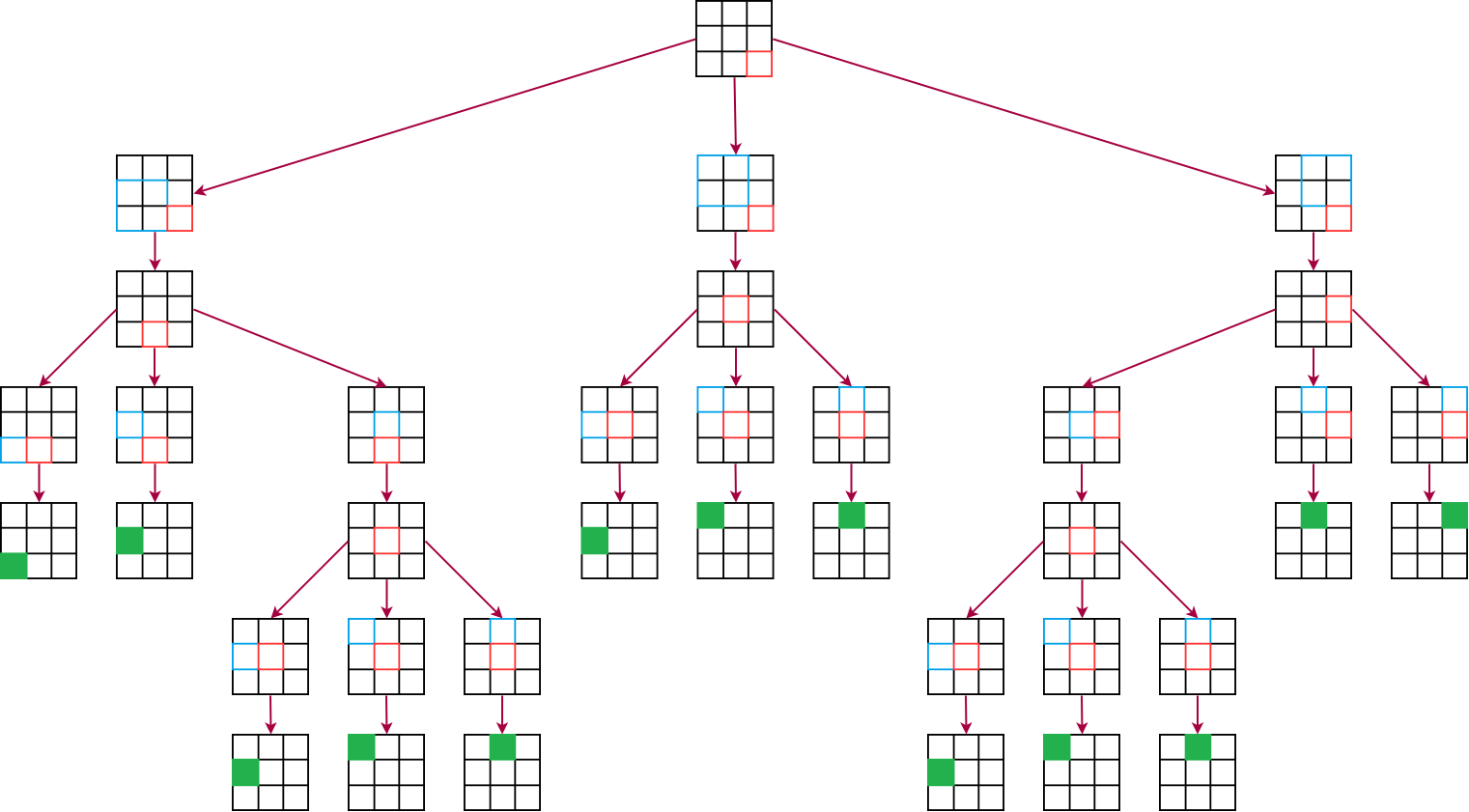
Avec cet exemple, on peut constater que des appels sont recommencés pour des valeurs de pixels sur le bord gauche ou sur la ligne du haut qui ont déjà été calculées :
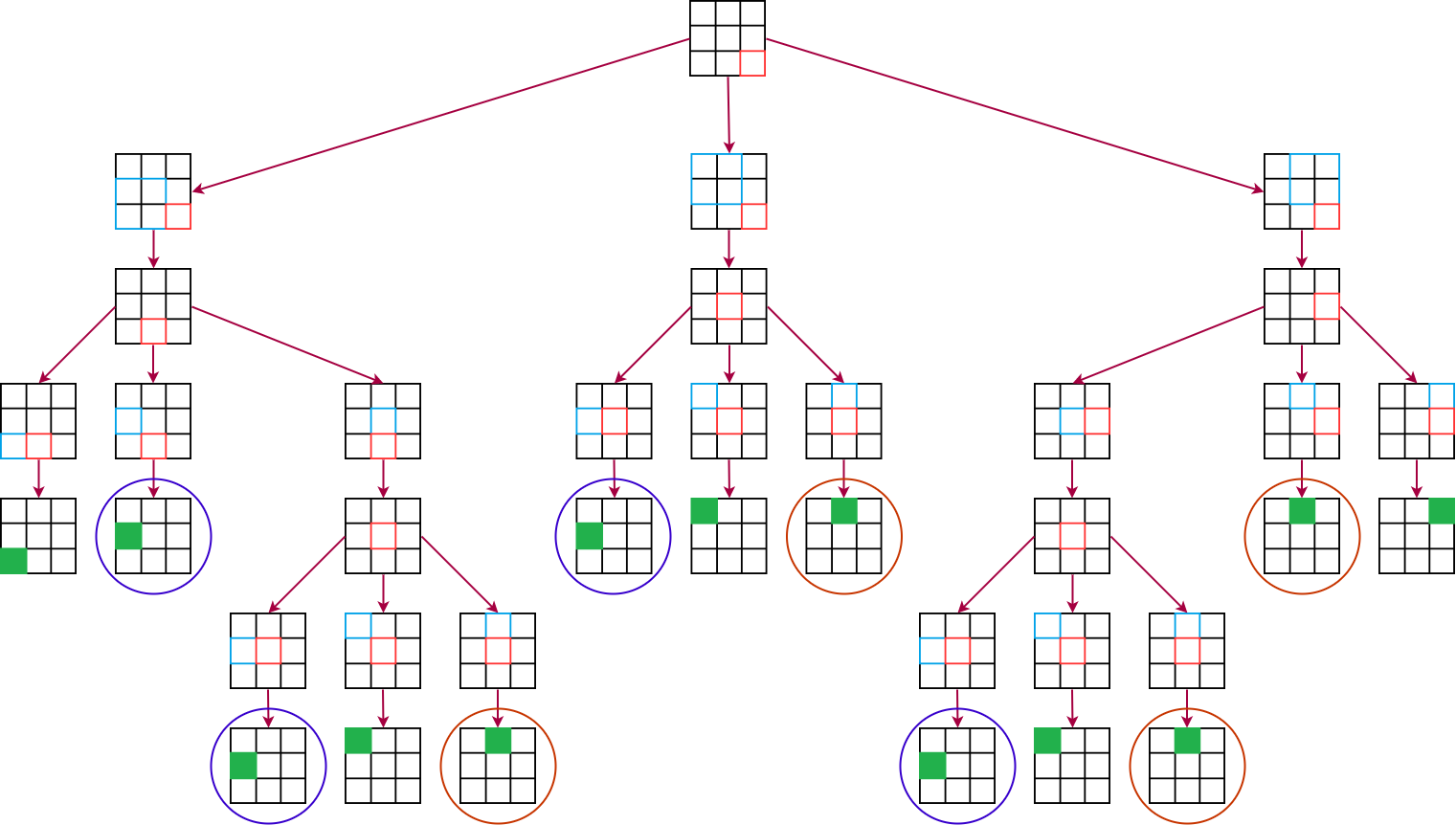
Encore pire, on recommence entièrement des appels récursifs qui ont déjà été réalisés auparavant :
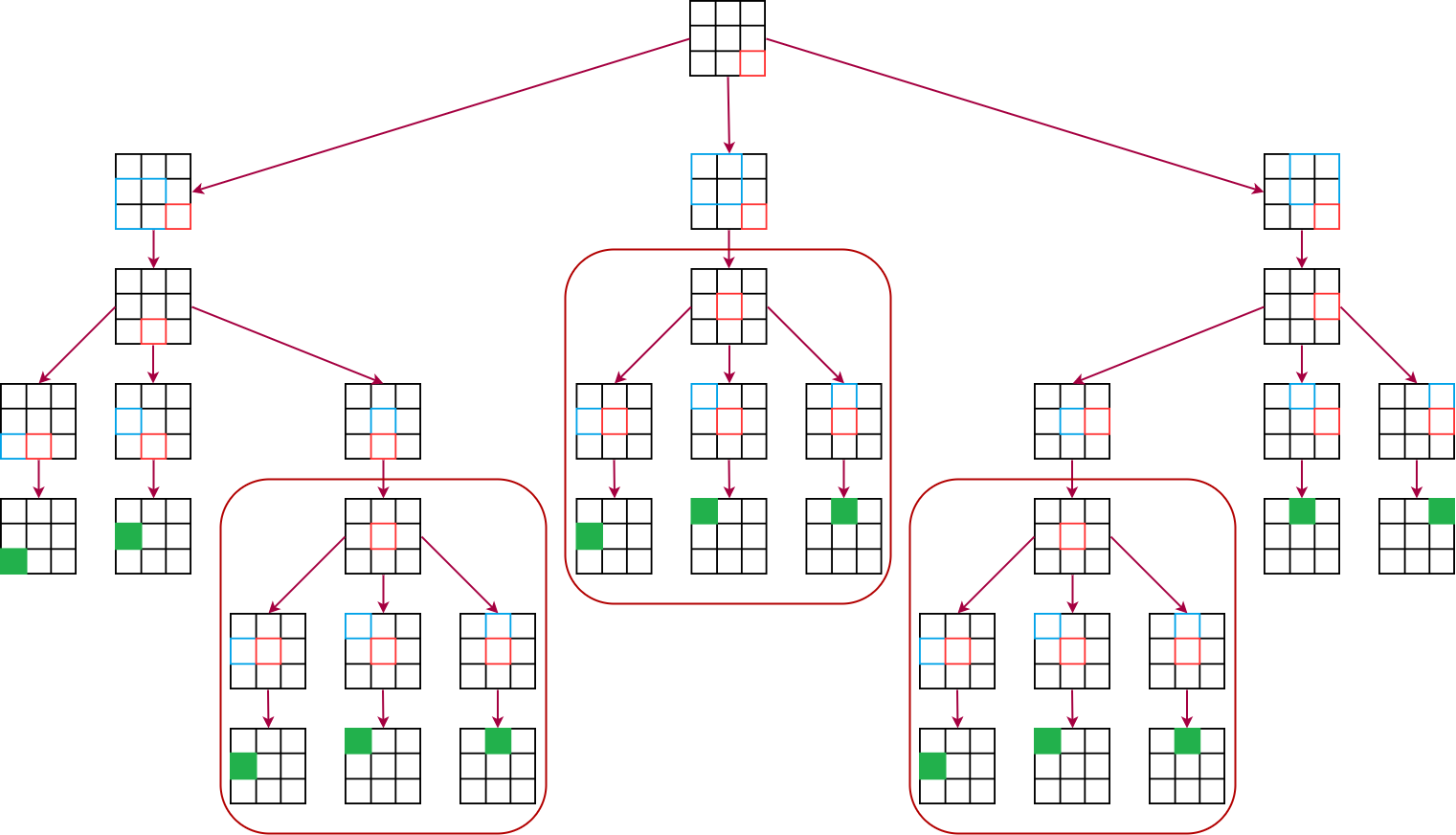
Ce phénomène explique que notre programme soit de plus en plus lent (et encore, notre exemple n'est constitué que d'une image en 12×12. Vous pouvez tester avec cette image en 15×15 : soyez très patients...).
Pour éviter cet encombrement de l'espace mémoire, l'exercice suivant va permettre d'améliorer ce programme en mémorisant les résultats dans le tableau dès qu'ils sont obtenus.
- Le pixel entouré de rouge est celui sur lequel la fonction
-
Question n°2 - mémoïsation☘
-
Complétez la nouvelle définition de la fonction
pgcb_rec()en respectant la spécification proposée1 2 3 4 5 6 7 8 9
def pgcb_rec(source, memo, x, y): """ source - référence d'une image carrée (au format 'L') déjà importée à l'aide de PIL au format 'L' La "couleur" d'un pixel noir est 0, celle d'un pixel blanc est 255 memo - tableau d'association entre chaque pixel de l'image et la longueur du côté du plus grand carré blanc qu'il permet de définir x, y - coordonnées entières du pixel en cours d'étude Sortie: valeur de memo[y][x] """Une solution
Attention à l'indentation du dernier
return...1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
def pgcb_rec(source, memo, x, y): """ source - référence d'une image carrée (au format 'L') déjà importée à l'aide de PIL au format 'L' La "couleur" d'un pixel noir est 0, celle d'un pixel blanc est 255 memo - tableau d'association entre chaque pixel de l'image et la longueur du côté du plus grand carré blanc qu'il permet de définir x, y - coordonnées entières du pixel en cours d'étude Sortie: valeur de memo[y][x] """ if memo[y][x] >= 0: return memo[y][x] else: couleur = source.getpixel( (x, y) ) if couleur == 0: memo[y][x] = 0 elif x==0 or y==0: memo[y][x] = 1 else: memo[y][x] = 1 + min(pgcb_rec(source, memo, x-1, y), pgcb_rec(source, memo, x-1, y-1), pgcb_rec(source, memo, x, y-1)) return memo[y][x] -
Complétez votre programme en lui ajoutant des lignes permettant de tester la fonction
pgcb_rec()en utilisant les images ou
ou  .
.Tableau renvoyé pour la première image
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1] [1, 2, 2, 2, 2, 0, 1, 2, 0, 1, 2, 2, 2, 2, 1, 1, 2, 2, 2, 2] [1, 2, 3, 0, 0, 1, 1, 2, 1, 1, 2, 3, 3, 0, 1, 2, 2, 3, 3, 3] [0, 1, 0, 1, 0, 0, 1, 2, 2, 2, 2, 3, 0, 1, 1, 2, 3, 3, 4, 4] [0, 1, 1, 1, 1, 0, 1, 2, 3, 3, 3, 0, 1, 1, 2, 2, 3, 4, 4, 5] [1, 1, 2, 2, 0, 1, 1, 2, 3, 4, 4, 1, 1, 2, 2, 3, 3, 4, 5, 5] [1, 2, 2, 3, 1, 1, 2, 2, 3, 4, 0, 1, 2, 2, 3, 3, 4, 4, 5, 6] [1, 2, 0, 1, 2, 0, 1, 0, 1, 2, 1, 1, 2, 3, 3, 4, 4, 5, 0, 1] [1, 0, 1, 0, 1, 1, 1, 0, 1, 2, 2, 2, 2, 3, 4, 4, 5, 5, 1, 1] [1, 0, 1, 1, 1, 2, 2, 1, 1, 2, 3, 3, 3, 3, 0, 1, 2, 3, 0, 1] [1, 1, 1, 2, 0, 1, 2, 2, 2, 2, 3, 4, 4, 0, 1, 1, 2, 3, 1, 1] [1, 2, 2, 2, 1, 1, 2, 3, 3, 3, 3, 4, 5, 0, 1, 2, 2, 3, 2, 0] [1, 2, 3, 3, 2, 2, 0, 1, 2, 3, 4, 4, 5, 1, 1, 2, 3, 3, 3, 1] [1, 2, 3, 4, 3, 3, 1, 1, 2, 3, 4, 5, 5, 2, 2, 2, 3, 0, 1, 2] [1, 2, 0, 1, 2, 3, 2, 2, 2, 3, 4, 5, 6, 0, 1, 2, 3, 1, 1, 2] [1, 2, 1, 1, 2, 3, 3, 0, 1, 2, 0, 1, 2, 1, 1, 2, 3, 2, 2, 2] [1, 2, 2, 2, 2, 3, 4, 1, 1, 2, 1, 1, 2, 0, 1, 2, 3, 0, 0, 1] [1, 2, 3, 3, 3, 3, 4, 0, 1, 2, 2, 0, 1, 1, 1, 2, 3, 1, 1, 1] [1, 0, 1, 2, 3, 4, 0, 1, 1, 2, 3, 1, 1, 2, 2, 2, 3, 2, 2, 0] [0, 1, 1, 2, 0, 1, 1, 0, 1, 2, 3, 2, 2, 2, 0, 1, 2, 3, 3, 1]Tableau renvoyé pour la seconde image
[1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1] [1, 2, 2, 2, 2, 2, 2, 1, 1, 2, 2, 2, 0, 1, 2, 2, 0, 0, 0, 0, 1, 2, 2, 2, 2, 0, 1, 1, 1, 2] [1, 2, 3, 3, 3, 3, 3, 0, 1, 2, 3, 3, 1, 1, 2, 3, 1, 1, 1, 1, 0, 1, 2, 3, 3, 1, 1, 0, 1, 2] [1, 2, 3, 4, 4, 4, 4, 1, 1, 2, 3, 4, 2, 2, 2, 3, 2, 2, 2, 0, 0, 1, 2, 3, 4, 2, 2, 0, 1, 2] [1, 2, 3, 4, 5, 5, 5, 2, 0, 1, 2, 3, 3, 3, 3, 3, 3, 3, 3, 0, 1, 0, 0, 1, 2, 0, 1, 1, 1, 0] [1, 2, 3, 4, 5, 6, 6, 3, 1, 1, 2, 3, 4, 4, 0, 1, 2, 3, 4, 1, 1, 1, 1, 0, 1, 1, 1, 2, 2, 1] [1, 2, 3, 4, 5, 6, 7, 4, 2, 2, 2, 3, 4, 5, 1, 0, 1, 2, 3, 2, 2, 2, 0, 1, 1, 2, 2, 2, 3, 0] [0, 1, 2, 3, 4, 5, 6, 5, 3, 3, 3, 3, 4, 5, 2, 1, 1, 2, 3, 3, 3, 3, 1, 1, 2, 2, 3, 0, 1, 1] [1, 1, 2, 3, 4, 5, 6, 6, 4, 4, 4, 4, 4, 5, 3, 2, 0, 0, 1, 2, 0, 1, 0, 1, 2, 3, 0, 1, 1, 0] [1, 2, 2, 3, 4, 5, 6, 7, 5, 0, 0, 1, 2, 3, 4, 3, 0, 1, 1, 2, 1, 0, 1, 1, 2, 3, 1, 1, 2, 1] [1, 2, 3, 3, 0, 1, 0, 1, 0, 1, 1, 1, 2, 3, 4, 4, 1, 1, 2, 2, 0, 1, 1, 2, 2, 0, 1, 2, 0, 1] [1, 2, 3, 4, 1, 1, 0, 1, 1, 1, 2, 2, 2, 0, 1, 2, 2, 2, 2, 3, 0, 1, 2, 2, 3, 1, 1, 2, 1, 1] [1, 2, 3, 4, 2, 2, 1, 1, 2, 2, 2, 0, 1, 1, 0, 1, 2, 3, 3, 3, 1, 0, 1, 0, 1, 2, 2, 2, 2, 2] [1, 2, 3, 0, 1, 2, 2, 2, 0, 0, 1, 1, 1, 2, 1, 1, 2, 3, 0, 1, 0, 1, 1, 0, 1, 2, 3, 3, 3, 3] [1, 2, 0, 1, 1, 2, 3, 3, 1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 1, 1, 1, 1, 0, 1, 1, 2, 3, 4, 4, 4] [1, 2, 1, 0, 1, 2, 3, 4, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 2, 2, 2, 2, 1, 1, 2, 2, 3, 4, 0, 1] [1, 2, 2, 1, 1, 2, 3, 4, 3, 3, 3, 3, 3, 4, 0, 1, 2, 3, 3, 3, 3, 3, 2, 2, 2, 3, 3, 4, 1, 1] [1, 2, 3, 2, 2, 2, 3, 4, 4, 4, 4, 0, 1, 2, 0, 1, 2, 0, 1, 2, 3, 4, 0, 1, 0, 1, 2, 0, 1, 2] [1, 2, 3, 3, 3, 0, 1, 2, 3, 4, 5, 1, 0, 0, 1, 1, 2, 1, 1, 2, 3, 4, 1, 1, 1, 0, 1, 1, 1, 2] [0, 1, 2, 3, 0, 1, 1, 2, 3, 4, 0, 1, 1, 1, 1, 2, 2, 0, 1, 2, 3, 4, 2, 2, 2, 1, 1, 2, 2, 2] [1, 1, 2, 3, 1, 1, 2, 2, 3, 4, 1, 1, 2, 2, 2, 2, 3, 1, 1, 2, 0, 1, 2, 3, 3, 2, 2, 2, 3, 3] [1, 2, 2, 3, 2, 2, 2, 0, 1, 2, 2, 2, 2, 3, 3, 3, 3, 2, 2, 2, 0, 1, 2, 3, 4, 3, 3, 3, 3, 4] [1, 2, 3, 3, 3, 3, 3, 1, 0, 1, 2, 3, 3, 3, 4, 4, 4, 0, 1, 2, 1, 1, 0, 1, 2, 3, 4, 4, 4, 4] [1, 2, 3, 4, 4, 4, 4, 0, 1, 1, 2, 3, 4, 4, 4, 5, 5, 1, 1, 2, 2, 2, 1, 1, 2, 3, 4, 5, 5, 5] [1, 2, 3, 4, 5, 5, 5, 1, 1, 0, 1, 2, 3, 4, 5, 5, 6, 2, 2, 2, 3, 3, 2, 2, 2, 3, 4, 5, 6, 6] [1, 0, 1, 2, 0, 0, 1, 2, 2, 0, 1, 2, 3, 4, 5, 6, 6, 3, 3, 0, 1, 2, 0, 1, 2, 3, 4, 5, 6, 7] [1, 1, 0, 1, 1, 1, 0, 1, 2, 1, 1, 2, 3, 4, 5, 6, 7, 4, 4, 1, 1, 2, 1, 1, 0, 1, 2, 3, 4, 5] [1, 2, 1, 1, 2, 2, 1, 1, 2, 2, 0, 1, 2, 3, 4, 5, 6, 5, 5, 2, 2, 2, 0, 1, 1, 1, 2, 3, 4, 5] [1, 2, 2, 2, 2, 3, 2, 2, 2, 0, 1, 1, 2, 3, 4, 5, 6, 6, 6, 3, 0, 1, 1, 1, 2, 2, 0, 0, 1, 2] [1, 2, 3, 3, 3, 3, 3, 3, 3, 1, 0, 0, 1, 2, 3, 4, 5, 6, 7, 4, 1, 1, 2, 2, 2, 3, 0, 1, 1, 2]Une solution
On peut commencer par initialiser à
-1chaque case d'un tableau denlignes etncolonnes, oùnest le nombre de pixels d'un des côtés de l'image carrée :1 2 3 4 5 6 7 8
source = Image.open('Ex_00_Image_12x12.png') largeur, hauteur = source.size memo = [[-1 for i in range(largeur)] for j in range(hauteur)] for x in range(largeur-1, -1, -1): for y in range(hauteur-1, -1, -1): memo[y][x] = pgcb_rec(source, memo, x, y) for ligne in memo: print(ligne)
Question n°3☘
-
A l'aide du travail réalisé dans la question précédente, réécrire le code de la fonction
recherche_pgcb_rec().Réponse du 1.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
def recherche_pgcb_rec(source): """ source - référence d'une image carrée (au format 'L') déjà importée à l'aide de PIL au format 'L' La "couleur" d'un pixel noir est 0, celle d'un pixel blanc est 255 Sortie: tuple - taille du côté du (ou des) plus grand(s) carré(s) blanc(s) de cette image et liste des coordonnées des coins haut/gauche de ceux-ci """ largeur, hauteur = source.size # Le tableau d'association est remplit de négatifs memo = [[-1 for i in range(largeur)] for j in range(hauteur)] # On complète récursivement le tableau d'association en partant de la dernière case : for x in range(largeur-1, -1, -1): for y in range(hauteur-1, -1, -1): memo[y][x] = pgcb_rec(source, memo, x, y) # On parcourt ce tableau pour déterminer les PGCB taille_max = 0 liste_coor = [] for x in range(largeur): for y in range(hauteur): if (taille_max != 0) and memo[x][y] == taille_max: liste_coor.append((y, x)) # Transposition elif memo[x][y] > taille_max: taille_max = memo[x][y] liste_coor = [(y, x)] # Transposition liste_coor = [(coor[0]-taille_max+1, coor[1]-taille_max+1) for coor in liste_coor] return (taille_max, liste_coor) -
En utilisant le module
time, comparez le temps de calcul de la fonctionrecherche_pgcb_rec(), avec celui des fonctionsrecherche_pgcb_iter(),recherche_pgcb_for(),recherche_pgcb_while()etrecherche_pgcb_glouton()pour chacune des images ci-dessous :Image n°1 Image n°2 Image n°3 


Réponse du 2.
Voici un exemple de résultats. On peut remarquer que l'algorithme dynamique récursif est très rapide et fiable en comparaison des algorithmes naïfs mais qu'il est un peu moins rapide que l'algorithme dynamique itératif :
Affichage des temps d'exécution pour trouver le plus grand carré blanc dans une image ===== Test des temps pour Image_100_40_test.png ===== (5, [(63, 11), (44, 72)]) Durée Boucle For : 1.198068380355835 secs (5, [(63, 11), (44, 72)]) Durée Boucle While : 0.239013671875 secs (3, [(3, 2)]) Durée Glouton : 0.0 secs (5, [(63, 11), (44, 72)]) Durée Dynamique Itératif : 0.021001100540161133 secs (5, [(63, 11), (44, 72)]) Durée Dynamique Récursif : 0.02800154685974121 secs ===== Test des temps pour Image_200_30_test.png ===== (6, [(60, 86)]) Durée Boucle For : 7.850449085235596 secs (6, [(60, 86)]) Durée Boucle While : 1.3810789585113525 secs (3, [(6, 2), (42, 2), (60, 2), (75, 2), (84, 2), (114, 2), (126, 2)]) Durée Glouton : 0.002000093460083008 secs (6, [(60, 86)]) Durée Dynamique Itératif : 0.08300471305847168 secs (6, [(60, 86)]) Durée Dynamique Récursif : 0.12200713157653809 secs ===== Test des temps pour Image_300_40_test.png ===== (5, [(117, 84), (223, 194), (134, 230)]) Durée Boucle For : 11.380650758743286 secs (5, [(117, 84), (223, 194), (134, 230)]) Durée Boucle While : 2.152122974395752 secs (3, [(42, 2)]) Durée Glouton : 0.002000093460083008 secs (5, [(117, 84), (223, 194), (134, 230)]) Durée Dynamique Itératif : 0.18301057815551758 secs (5, [(117, 84), (223, 194), (134, 230)]) Durée Dynamique Récursif : 0.2590148448944092 secsVous trouverez ci-dessous un exemple de programme permettant d'obtenir ces résultats :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252
from PIL import Image import time # Fonctions def recherche_pgcb_for(source): """ source - référence d'une image carrée (au format 'L') déjà importée à l'aide de PIL au format 'L' La "couleur" d'un pixel noir est 0, celle d'un pixel blanc est 255 Sortie: list - tableau d'association entre chaque pixel de l'image et la longueur du côté du plus grand carré blanc qu'il permet de définir """ largeur, hauteur = source.size # L'image est carrée donc largeur = hauteur coordonnees = [] taille_max = 1 for taille_max in range(1, min(largeur, hauteur)): # On cherche un carré. On aurait pu écrire largeur au lieu de min(largeur, hauteur) if taille_max == 1: # La détection d'un carré de 1px de côté est plus simple for y in range(hauteur): for x in range(largeur): if source.getpixel((x,y)) == 255: # Si je trouve un blanc j'ajoute à la liste coordonnees.append((x, y)) else: # Détection carré > 1px for y in range(hauteur - taille_max): for x in range(largeur - taille_max): coin = (x,y) compte = 0 # compteur de pixels noirs for j in range(0,taille_max): for i in range(0,taille_max): if source.getpixel((x+i,y+j)) != 255: # si c'est différent d'un pixel blanc compte += 1 if compte == 0: # si que des pixels blanc coordonnees.append(coin) if len(coordonnees) == 0: # Une taille de carrée plus grande ne retourne rien return taille_max-1, liste_a_retourner # Je retourne la liste précédente, décrémenter de 1 à cause de mon passage sans rien trouver à taille_max+1 else: liste_a_retourner = coordonnees # Je stocke l'état de coordonnees pour un éventuel return dans la boucle d'après taille_max += 1 # je passe à la taille à détecter suivante coordonnees = [] # Je remets à zéro ma liste def recherche_pgcb_while(source): """ source - référence d'une image carrée (au format 'L') déjà importée à l'aide de PIL au format 'L' La "couleur" d'un pixel noir est 0, celle d'un pixel blanc est 255 Sortie: list - tableau d'association entre chaque pixel de l'image et la longueur du côté du plus grand carré blanc qu'il permet de définir """ largeur, hauteur = source.size # L'image est carrée donc largeur = hauteur coordonnees = [] taille_max = 1 for taille_max in range(1, min(largeur, hauteur)): # On cherche un carré. On aurait pu écrire largeur au lieu de min(largeur, hauteur) if taille_max == 1: # La détection d'un carré de 1px de côté est plus simple for y in range(hauteur): for x in range(largeur): if source.getpixel((x,y)) == 255: # Si je trouve un blanc j'ajoute à la liste coordonnees.append((x, y)) else: # Détection carré > 1px for y in range(hauteur - taille_max): for x in range(largeur - taille_max): coin = (x,y) j = 0 compte = 0 # compteur de pixels noirs while compte == 0 and j < taille_max: i = 0 while compte == 0 and i < taille_max: if source.getpixel((x+i,y+j)) != 255: compte += 1 i += 1 j += 1 if compte == 0: # si que des pixels blanc coordonnees.append(coin) if len(coordonnees) == 0: # Une taille de carrée plus grande ne retourne rien return taille_max-1, liste_a_retourner # Je retourne la liste précédente, décrémenter de 1 à cause de mon passage sans rien trouver à taille_max+1 else: liste_a_retourner = coordonnees # Je stocke l'état de coordonnees pour un éventuel return dans la boucle d'après taille_max += 1 # je passe à la taille à détecter suivante coordonnees = [] # Je remets à zéro ma liste def recherche_pgcb_glouton(source): """ source - référence d'une image carrée (au format 'L') déjà importée à l'aide de PIL au format 'L' La "couleur" d'un pixel noir est 0, celle d'un pixel blanc est 255 Sortie: list - tableau d'association entre chaque pixel de l'image et la longueur du côté du plus grand carré blanc qu'il permet de définir """ largeur, hauteur = source.size # L'image est carrée donc largeur = hauteur coordonnees = [] taille_max = 1 for y in range(0, hauteur - taille_max, taille_max): for x in range(0, largeur - taille_max, taille_max): coin = (x,y) j = 0 compte = 0 # compteur de pixels noirs while compte == 0 and j < taille_max: i = 0 while compte == 0 and i < taille_max: if source.getpixel((x+i,y+j)) != 255: compte += 1 i += 1 j += 1 if compte == 0: # si que des pixels blanc coordonnees.append(coin) if len(coordonnees) == 0: # Une taille de carrée plus grande ne retourne rien return taille_max-1, liste_a_retourner # Je retourne la liste précédente, décrémenter de 1 à cause de mon passage sans rien trouver à taille_max+1 else: liste_a_retourner = coordonnees # Je stocke l'état de coordonnees pour un éventuel return dans la boucle d'après taille_max += 1 # je passe à la taille à détecter suivante coordonnees = [] def pgcb_iter(source): """ source - référence d'une image carrée (au format 'L') déjà importée à l'aide de PIL au format 'L' La "couleur" d'un pixel noir est 0, celle d'un pixel blanc est 255 Sortie: list - tableau d'association entre chaque pixel de l'image et la longueur du côté du plus grand carré blanc qu'il permet de définir """ largeur, hauteur = source.size # On initialise tous les pixels comme s'ils étaient noirs memo = [[0 for y in range(largeur)] for x in range(hauteur)] for x in range(largeur): # parcours des abscisses for y in range(largeur): # parcours des ordonnées couleur = source.getpixel( (x, y) ) if couleur == 0: # Test inutile par initialisation mais important à écrire # car il correspond au 1er cas de la relation de récurrence memo[y][x] = 0 # Transposition elif (x == 0) or (y == 0): memo[y][x] = 1 else: memo[y][x] = 1 + min(memo[y][x-1], memo[y-1][x-1], memo[y-1][x]) return memo def recherche_pgcb_iter(source): """ source - référence d'une image carrée (au format 'L') déjà importée à l'aide de PIL au format 'L' La "couleur" d'un pixel noir est 0, celle d'un pixel blanc est 255 Sortie: tuple - taille du côté du (ou des) plus grand(s) carré(s) blanc(s) de cette image et liste des coordonnées des coins haut/gauche de ceux-ci """ largeur, hauteur = source.size # Création de la matrice de memoisation memo = pgcb_iter(source) taille_max = 0 liste_coor = [] for x in range(largeur): for y in range(hauteur): if (taille_max != 0) and memo[x][y] == taille_max: liste_coor.append((y, x)) # Transposition elif memo[x][y] > taille_max: taille_max = memo[x][y] liste_coor = [(y, x)] # Transposition liste_coor = [(coor[0]-taille_max+1, coor[1]-taille_max+1) for coor in liste_coor] return (taille_max, liste_coor) def pgcb_rec(source, memo, x, y): """ source - référence d'une image carrée (au format 'L') déjà importée à l'aide de PIL au format 'L' La "couleur" d'un pixel noir est 0, celle d'un pixel blanc est 255 memo - tableau d'association entre chaque pixel de l'image et la longueur du côté du plus grand carré blanc qu'il permet de définir x, y - coordonnées entières du pixel en cours d'étude Sortie: valeur de memo[y][x] """ if memo[y][x] >= 0: return memo[y][x] else: couleur = source.getpixel( (x, y) ) if couleur == 0: memo[y][x] = 0 elif x==0 or y==0: memo[y][x] = 1 else: memo[y][x] = 1 + min(pgcb_rec(source, memo, x-1, y), pgcb_rec(source, memo, x-1, y-1), pgcb_rec(source, memo, x, y-1)) return memo[y][x] def recherche_pgcb_rec(source): """ source - référence d'une image carrée (au format 'L') déjà importée à l'aide de PIL au format 'L' La "couleur" d'un pixel noir est 0, celle d'un pixel blanc est 255 Sortie: tuple - taille du côté du (ou des) plus grand(s) carré(s) blanc(s) de cette image et liste des coordonnées des coins haut/gauche de ceux-ci """ largeur, hauteur = source.size # Le tableau d'association est remplit de négatifs memo = [[-1 for i in range(largeur)] for j in range(hauteur)] # On complète récursivement le tableau d'association en partant de la dernière case : for x in range(largeur-1, -1, -1): for y in range(hauteur-1, -1, -1): memo[y][x] = pgcb_rec(source, memo, x, y) # On parcourt ce tableau pour déterminer les PGCB taille_max = 0 liste_coor = [] for x in range(largeur): for y in range(hauteur): if (taille_max != 0) and memo[x][y] == taille_max: liste_coor.append((y, x)) # Transposition elif memo[x][y] > taille_max: taille_max = memo[x][y] liste_coor = [(y, x)] # Transposition liste_coor = [(coor[0]-taille_max+1, coor[1]-taille_max+1) for coor in liste_coor] return (taille_max, liste_coor) ############################## ### Programme Principal ###### ############################## noms = ['Image_100_40_test.png', 'Image_200_30_test.png', 'Image_300_40_test.png'] print("Affichage des temps d'exécution pour trouver le plus grand carré blanc dans une image") for nom_fichier in noms : print(f'===== Test des temps pour {nom_fichier} =====\n') source = Image.open(nom_fichier) start = time.time() print(recherche_pgcb_for(source)) end = time.time() print(f"Durée Boucle For : {end - start} secs") start = time.time() print(recherche_pgcb_while(source)) end = time.time() print(f"Durée Boucle While : {end - start} secs") start = time.time() print(recherche_pgcb_glouton(source)) end = time.time() print(f"Durée Glouton : {end - start} secs") start = time.time() print(recherche_pgcb_iter(source)) end = time.time() print(f"Durée Dynamique Itératif : {end - start} secs") start = time.time() print(recherche_pgcb_rec(source)) end = time.time() print(f"Durée Dynamique Récursif : {end - start} secs") print('\n\n')