Aller au contenu

Programmation dynamique itérative☘

Modélisation☘

Dans la partie précédente, nous avons associé un pixel de l'image à une valeur entière :

  • 0 si ce pixel est noir,
  • 1 s'il est le coin bas-droite d'un carré blanc de côté 1 ;
  • 2 s'il est le coin bas-droite d'un carré blanc de côté 2 ;
  • etc...

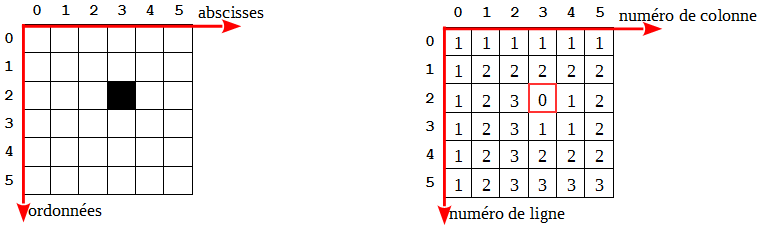
Ainsi, l'image ci-dessous à gauche peut être modélisée par le tableau ci-dessous à droite : image pixels

En Python, le tableau de droite va être modélisé sous la forme d'un tableau de tableau (une matrice) nommée memo (par exemple) et sera défini ainsi : 

1
2
3
4
5
6
memo = [[1, 1, 1, 1, 1, 1],
        [1, 2, 2, 2, 2, 2],
        [1, 2, 3, 0, 1, 2],
        [1, 2, 3, 1, 1, 2],
        [1, 2, 3, 2, 2, 2],
        [1, 2, 3, 3, 3, 3] ]

  • Dans l'image de gauche, les coordonnées du pixel noir sont (3, 2) : on donne d'abord l'abscisse, puis l'ordonnée.
  • Dans le tableau de droite, qui modélise l'image, la valeur « 0 » représente le pixel noir. « 0 » est donc la valeur de l'élément memo[2][3] : on écrit d'abord le numéro de ligne, puis le numéro de colonne.

A retenir

Le pixel (x, y) de l'image sera associé à un entier placé dans la case memo[y][x] du tableau.

Rappel☘

On désigne par memo le tableau qui, à une image carrée composée de pixels noirs et blancs, associe pour chaque pixel (x, y) une valeur entière selon la relation de récurrence suivante :

Relation de récurrence

  • Si le pixel (x, y) est noir, alors
    memo[y][x] = 0.
  • Si (x, y) est blanc et qu'il appartient à la première ligne (en haut) ou la première colonne (à gauche), alors
    memo[y][x] = 1.
  • Si (x, y) est blanc et qu'il n'est pas dans le cas précédent, alors
    memo[y][x] = 1 + min(memo[y][x-1], memo[y-1][x-1], memo[y-1][x]).

Question n°1☘

A l'aide de la relation de récurrence précédente, complétez le code de la fonction pgcb_iter() spécifiée ci-dessous afin qu'elle renvoie le tableau memo associé à l'image source.

1
2
3
4
5
6
7
def pgcb_iter(source):
    """
    source - référence d'une image carrée (au format 'L') déjà importée à l'aide de PIL au format 'L'
            La "couleur" d'un pixel noir est 0, celle d'un pixel blanc est 255
    Sortie: list - tableau d'association entre chaque pixel de l'image et la longueur
            du côté du plus grand carré blanc qu'il permet de définir
    """
Un premier exemple pour tester

Effectuez un clic droit sur l'image ci-contre afin de l'enregistrer . Voici une version agrandie de cette image : Exemple 01 agrandi

Vérifiez que le tableau renvoyé pour cette image est : 

[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1]
[1, 2, 2, 2, 2, 0, 1, 2, 0, 1, 2, 2, 2, 2, 1, 1, 2, 2, 2, 2]
[1, 2, 3, 0, 0, 1, 1, 2, 1, 1, 2, 3, 3, 0, 1, 2, 2, 3, 3, 3]
[0, 1, 0, 1, 0, 0, 1, 2, 2, 2, 2, 3, 0, 1, 1, 2, 3, 3, 4, 4]
[0, 1, 1, 1, 1, 0, 1, 2, 3, 3, 3, 0, 1, 1, 2, 2, 3, 4, 4, 5]
[1, 1, 2, 2, 0, 1, 1, 2, 3, 4, 4, 1, 1, 2, 2, 3, 3, 4, 5, 5]
[1, 2, 2, 3, 1, 1, 2, 2, 3, 4, 0, 1, 2, 2, 3, 3, 4, 4, 5, 6]
[1, 2, 0, 1, 2, 0, 1, 0, 1, 2, 1, 1, 2, 3, 3, 4, 4, 5, 0, 1]
[1, 0, 1, 0, 1, 1, 1, 0, 1, 2, 2, 2, 2, 3, 4, 4, 5, 5, 1, 1]
[1, 0, 1, 1, 1, 2, 2, 1, 1, 2, 3, 3, 3, 3, 0, 1, 2, 3, 0, 1]
[1, 1, 1, 2, 0, 1, 2, 2, 2, 2, 3, 4, 4, 0, 1, 1, 2, 3, 1, 1]
[1, 2, 2, 2, 1, 1, 2, 3, 3, 3, 3, 4, 5, 0, 1, 2, 2, 3, 2, 0]
[1, 2, 3, 3, 2, 2, 0, 1, 2, 3, 4, 4, 5, 1, 1, 2, 3, 3, 3, 1]
[1, 2, 3, 4, 3, 3, 1, 1, 2, 3, 4, 5, 5, 2, 2, 2, 3, 0, 1, 2]
[1, 2, 0, 1, 2, 3, 2, 2, 2, 3, 4, 5, 6, 0, 1, 2, 3, 1, 1, 2]
[1, 2, 1, 1, 2, 3, 3, 0, 1, 2, 0, 1, 2, 1, 1, 2, 3, 2, 2, 2]
[1, 2, 2, 2, 2, 3, 4, 1, 1, 2, 1, 1, 2, 0, 1, 2, 3, 0, 0, 1]
[1, 2, 3, 3, 3, 3, 4, 0, 1, 2, 2, 0, 1, 1, 1, 2, 3, 1, 1, 1]
[1, 0, 1, 2, 3, 4, 0, 1, 1, 2, 3, 1, 1, 2, 2, 2, 3, 2, 2, 0]
[0, 1, 1, 2, 0, 1, 1, 0, 1, 2, 3, 2, 2, 2, 0, 1, 2, 3, 3, 1]

Un second exemple pour tester

Effectuez un clic droit sur l'image ci-contre afin de l'enregistrer . Voici une version agrandie de cette image : Exemple 02 agrandi

Vérifiez que le tableau renvoyé pour cette image est : 

[1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1]
[1, 2, 2, 2, 2, 2, 2, 1, 1, 2, 2, 2, 0, 1, 2, 2, 0, 0, 0, 0, 1, 2, 2, 2, 2, 0, 1, 1, 1, 2]
[1, 2, 3, 3, 3, 3, 3, 0, 1, 2, 3, 3, 1, 1, 2, 3, 1, 1, 1, 1, 0, 1, 2, 3, 3, 1, 1, 0, 1, 2]
[1, 2, 3, 4, 4, 4, 4, 1, 1, 2, 3, 4, 2, 2, 2, 3, 2, 2, 2, 0, 0, 1, 2, 3, 4, 2, 2, 0, 1, 2]
[1, 2, 3, 4, 5, 5, 5, 2, 0, 1, 2, 3, 3, 3, 3, 3, 3, 3, 3, 0, 1, 0, 0, 1, 2, 0, 1, 1, 1, 0]
[1, 2, 3, 4, 5, 6, 6, 3, 1, 1, 2, 3, 4, 4, 0, 1, 2, 3, 4, 1, 1, 1, 1, 0, 1, 1, 1, 2, 2, 1]
[1, 2, 3, 4, 5, 6, 7, 4, 2, 2, 2, 3, 4, 5, 1, 0, 1, 2, 3, 2, 2, 2, 0, 1, 1, 2, 2, 2, 3, 0]
[0, 1, 2, 3, 4, 5, 6, 5, 3, 3, 3, 3, 4, 5, 2, 1, 1, 2, 3, 3, 3, 3, 1, 1, 2, 2, 3, 0, 1, 1]
[1, 1, 2, 3, 4, 5, 6, 6, 4, 4, 4, 4, 4, 5, 3, 2, 0, 0, 1, 2, 0, 1, 0, 1, 2, 3, 0, 1, 1, 0]
[1, 2, 2, 3, 4, 5, 6, 7, 5, 0, 0, 1, 2, 3, 4, 3, 0, 1, 1, 2, 1, 0, 1, 1, 2, 3, 1, 1, 2, 1]
[1, 2, 3, 3, 0, 1, 0, 1, 0, 1, 1, 1, 2, 3, 4, 4, 1, 1, 2, 2, 0, 1, 1, 2, 2, 0, 1, 2, 0, 1]
[1, 2, 3, 4, 1, 1, 0, 1, 1, 1, 2, 2, 2, 0, 1, 2, 2, 2, 2, 3, 0, 1, 2, 2, 3, 1, 1, 2, 1, 1]
[1, 2, 3, 4, 2, 2, 1, 1, 2, 2, 2, 0, 1, 1, 0, 1, 2, 3, 3, 3, 1, 0, 1, 0, 1, 2, 2, 2, 2, 2]
[1, 2, 3, 0, 1, 2, 2, 2, 0, 0, 1, 1, 1, 2, 1, 1, 2, 3, 0, 1, 0, 1, 1, 0, 1, 2, 3, 3, 3, 3]
[1, 2, 0, 1, 1, 2, 3, 3, 1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 1, 1, 1, 1, 0, 1, 1, 2, 3, 4, 4, 4]
[1, 2, 1, 0, 1, 2, 3, 4, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 2, 2, 2, 2, 1, 1, 2, 2, 3, 4, 0, 1]
[1, 2, 2, 1, 1, 2, 3, 4, 3, 3, 3, 3, 3, 4, 0, 1, 2, 3, 3, 3, 3, 3, 2, 2, 2, 3, 3, 4, 1, 1]
[1, 2, 3, 2, 2, 2, 3, 4, 4, 4, 4, 0, 1, 2, 0, 1, 2, 0, 1, 2, 3, 4, 0, 1, 0, 1, 2, 0, 1, 2]
[1, 2, 3, 3, 3, 0, 1, 2, 3, 4, 5, 1, 0, 0, 1, 1, 2, 1, 1, 2, 3, 4, 1, 1, 1, 0, 1, 1, 1, 2]
[0, 1, 2, 3, 0, 1, 1, 2, 3, 4, 0, 1, 1, 1, 1, 2, 2, 0, 1, 2, 3, 4, 2, 2, 2, 1, 1, 2, 2, 2]
[1, 1, 2, 3, 1, 1, 2, 2, 3, 4, 1, 1, 2, 2, 2, 2, 3, 1, 1, 2, 0, 1, 2, 3, 3, 2, 2, 2, 3, 3]
[1, 2, 2, 3, 2, 2, 2, 0, 1, 2, 2, 2, 2, 3, 3, 3, 3, 2, 2, 2, 0, 1, 2, 3, 4, 3, 3, 3, 3, 4]
[1, 2, 3, 3, 3, 3, 3, 1, 0, 1, 2, 3, 3, 3, 4, 4, 4, 0, 1, 2, 1, 1, 0, 1, 2, 3, 4, 4, 4, 4]
[1, 2, 3, 4, 4, 4, 4, 0, 1, 1, 2, 3, 4, 4, 4, 5, 5, 1, 1, 2, 2, 2, 1, 1, 2, 3, 4, 5, 5, 5]
[1, 2, 3, 4, 5, 5, 5, 1, 1, 0, 1, 2, 3, 4, 5, 5, 6, 2, 2, 2, 3, 3, 2, 2, 2, 3, 4, 5, 6, 6]
[1, 0, 1, 2, 0, 0, 1, 2, 2, 0, 1, 2, 3, 4, 5, 6, 6, 3, 3, 0, 1, 2, 0, 1, 2, 3, 4, 5, 6, 7]
[1, 1, 0, 1, 1, 1, 0, 1, 2, 1, 1, 2, 3, 4, 5, 6, 7, 4, 4, 1, 1, 2, 1, 1, 0, 1, 2, 3, 4, 5]
[1, 2, 1, 1, 2, 2, 1, 1, 2, 2, 0, 1, 2, 3, 4, 5, 6, 5, 5, 2, 2, 2, 0, 1, 1, 1, 2, 3, 4, 5]
[1, 2, 2, 2, 2, 3, 2, 2, 2, 0, 1, 1, 2, 3, 4, 5, 6, 6, 6, 3, 0, 1, 1, 1, 2, 2, 0, 0, 1, 2]
[1, 2, 3, 3, 3, 3, 3, 3, 3, 1, 0, 0, 1, 2, 3, 4, 5, 6, 7, 4, 1, 1, 2, 2, 2, 3, 0, 1, 1, 2]

Une piste

On peut commencer par initialiser un tableau de n lignes et n colonnes, où n est le nombre de pixels d'un des côtés de l'image carrée

Une solution
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def pgcb_iter(source):
    """
    source - référence d'une image carrée (au format 'L') déjà importée à l'aide de PIL au format 'L'
            La "couleur" d'un pixel noir est 0, celle d'un pixel blanc est 255
    Sortie: list - tableau d'association entre chaque pixel de l'image et la longueur
            du côté du plus grand carré blanc qu'il permet de définir
    """
    largeur, hauteur = source.size
    # On initialise tous les pixels comme s'ils étaient noirs
    memo = [[0 for y in range(largeur)] for x in range(hauteur)]

    for x in range(largeur):            # parcours des abscisses
        for y in range(largeur):        # parcours des ordonnées
            couleur = source.getpixel( (x, y) )

            if couleur == 0:            # Test inutile par initialisation mais important à écrire
                                        # car il correspond au 1er cas de la relation de récurrence
                memo[y][x] = 0          # Transposition
            elif (x == 0) or (y == 0):
                memo[y][x] = 1
            else:
                memo[y][x] = 1 + min(memo[y][x-1], memo[y-1][x-1], memo[y-1][x])
    return memo

Question n°2☘

Une lecture du tableau memo permet de rapidement identifier la taille des plus grands carrés blancs et leur position. Ainsi :

  • pour cette première image (à gauche), on peut identifier les carrés mis en valeur à droite : Mise en valeur

  • pour cette seconde image (à gauche), on peut identifier les carrés mis en valeur à droite : Mise en valeur

En utilisant la fonction pgcb_iter() programmée dans la question précédente, complétez le code de la fonction recherche_pgcb qui renvoie la taille (en pixels) d'un côté du plus grand carré blanc de l'image, ainsi que la listes des pixels haut-gauche de ce (ou ces) carré(s).

1
2
3
4
5
6
7
def recherche_pgcb_iter(source):
    """
    source - référence d'une image carrée (au format 'L') déjà importée à l'aide de PIL au format 'L'
            La "couleur" d'un pixel noir est 0, celle d'un pixel blanc est 255
    Sortie: tuple - taille du côté du (ou des) plus grand(s) carré(s) blanc(s) de cette image
            et liste des coordonnées des coins haut/gauche de ceux-ci
    """
Un premier exemple pour tester

Avec l'image ci-contre dont la version agrandie est : Exemple 01 agrandi

on obtient le tuple : 

(6, [(14, 1), (7, 9)])

Un second exemple pour tester

Avec l'image ci-contre dont la version agrandie est : Exemple 02 agrandi

on obtient le tuple : 

(7, [(0, 0), (1, 3), (23, 19), (10, 20), (12, 23)])

Une piste

On peut commencer par rechercher la liste des coordonnées des pixels bas/droite.

  • Pour l'exemple n°1, cette liste est : [(19, 6), (12, 14)].
  • Pour l'exemple n°2, cette liste est : [(6, 6), (7, 9), (29, 35), (16, 26), (18, 29)].
Une solution

On a le tableau des coordonnées des pixels bas-droite ainsi que la dimension des côtés des plus grands carrés blancs. On peut donc en déduire les coordonnées des pixels haut-gauche de ces carrés... 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
def recherche_pgcb_iter(source):
    """
    source - référence d'une image carrée (au format 'L') déjà importée à l'aide de PIL au format 'L'
            La "couleur" d'un pixel noir est 0, celle d'un pixel blanc est 255
    Sortie: tuple - taille du côté du (ou des) plus grand(s) carré(s) blanc(s) de cette image
            et liste des coordonnées des coins haut/gauche de ceux-ci
    """
    largeur, hauteur = source.size
    # Création du tableau d'association
    memo = pgcb_iter(source)

    taille_max = 0
    liste_coor = []
    for x in range(largeur):
        for y in range(hauteur):
            if (taille_max != 0) and memo[x][y] == taille_max:
                liste_coor.append((y, x))       # Transposition
            elif memo[x][y] > taille_max:
                taille_max = memo[x][y]
                liste_coor = [(y, x)]           # Transposition
    liste_coor = [(coor[0]-taille_max+1, coor[1]-taille_max+1) for coor in liste_coor]
    return (taille_max, liste_coor)

Question n°3☘

En utilisant le module time, comparez le temps de calcul de la fonction recherche_pgcb_iter() avec celui des fonctions recherche_pgcb_for(), recherche_pgcb_while() et recherche_pgcb_glouton() pour chacune des images ci-dessous :

Image n°1 Image n°2 Image n°3
alt text alt text alt text
Programmes à comparer
  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
from PIL import Image
import time

# Fonctions

def recherche_pgcb_for(source):
    """
    source - référence d'une image carrée (au format 'L') déjà importée à l'aide de PIL au format 'L'
            La "couleur" d'un pixel noir est 0, celle d'un pixel blanc est 255
    Sortie: list - tableau d'association entre chaque pixel de l'image et la longueur
            du côté du plus grand carré blanc qu'il permet de définir
    """
    largeur, hauteur = source.size                          # L'image est carrée donc largeur = hauteur
    coordonnees = []
    taille_max = 1
    for taille_max in range(1, min(largeur, hauteur)):      # On cherche un carré. On aurait pu écrire largeur au lieu de min(largeur, hauteur)
        if taille_max == 1:                                 # La détection d'un carré de 1px de côté est plus simple
            for y in range(hauteur):
                for x in range(largeur):
                    if source.getpixel((x,y)) == 255:       # Si je trouve un blanc j'ajoute à la liste
                        coordonnees.append((x, y))

        else:                                               # Détection carré > 1px
            for y in range(hauteur - taille_max):
                for x in range(largeur - taille_max):
                    coin = (x,y)
                    compte = 0                              # compteur de pixels noirs
                    for j in range(0,taille_max):
                        for i in range(0,taille_max):
                            if source.getpixel((x+i,y+j)) != 255:   # si c'est différent d'un pixel blanc
                                compte += 1
                    if compte == 0:                                 # si que des pixels blanc
                        coordonnees.append(coin)

        if len(coordonnees) == 0:                           # Une taille de carrée plus grande ne retourne rien
            return taille_max-1, liste_a_retourner          # Je retourne la liste précédente, décrémenter de 1 à cause de mon passage sans rien trouver à taille_max+1
        else:
            liste_a_retourner = coordonnees                 # Je stocke l'état de coordonnees pour un éventuel return dans la boucle d'après
            taille_max += 1                                 # je passe à la taille à détecter suivante
            coordonnees = []                                # Je remets à zéro ma liste


def recherche_pgcb_while(source):
    """
    source - référence d'une image carrée (au format 'L') déjà importée à l'aide de PIL au format 'L'
            La "couleur" d'un pixel noir est 0, celle d'un pixel blanc est 255
    Sortie: list - tableau d'association entre chaque pixel de l'image et la longueur
            du côté du plus grand carré blanc qu'il permet de définir
    """
    largeur, hauteur = source.size                          # L'image est carrée donc largeur = hauteur
    coordonnees = []
    taille_max = 1
    for taille_max in range(1, min(largeur, hauteur)):      # On cherche un carré. On aurait pu écrire largeur au lieu de min(largeur, hauteur)
        if taille_max == 1:                                 # La détection d'un carré de 1px de côté est plus simple
            for y in range(hauteur):
                for x in range(largeur):
                    if source.getpixel((x,y)) == 255:       # Si je trouve un blanc j'ajoute à la liste
                        coordonnees.append((x, y))
        else:                                               # Détection carré > 1px
            for y in range(hauteur - taille_max):
                for x in range(largeur - taille_max):
                    coin = (x,y)
                    j = 0
                    compte = 0                              # compteur de pixels noirs
                    while compte == 0 and j < taille_max:
                        i = 0
                        while compte == 0 and i < taille_max:
                            if source.getpixel((x+i,y+j)) != 255:
                                compte += 1
                            i += 1
                        j += 1
                    if compte == 0:                         # si que des pixels blanc
                        coordonnees.append(coin)
        if len(coordonnees) == 0:                           # Une taille de carrée plus grande ne retourne rien
            return taille_max-1, liste_a_retourner          # Je retourne la liste précédente, décrémenter de 1 à cause de mon passage sans rien trouver à taille_max+1
        else:
            liste_a_retourner = coordonnees                 # Je stocke l'état de coordonnees pour un éventuel return dans la boucle d'après
            taille_max += 1                                 # je passe à la taille à détecter suivante
            coordonnees = []                                # Je remets à zéro ma liste


def recherche_pgcb_glouton(source):
    """
    source - référence d'une image carrée (au format 'L') déjà importée à l'aide de PIL au format 'L'
            La "couleur" d'un pixel noir est 0, celle d'un pixel blanc est 255
    Sortie: list - tableau d'association entre chaque pixel de l'image et la longueur
            du côté du plus grand carré blanc qu'il permet de définir
    """
    largeur, hauteur = source.size                          # L'image est carrée donc largeur = hauteur
    coordonnees = []
    taille_max = 1
    for y in range(0, hauteur - taille_max, taille_max):
        for x in range(0, largeur - taille_max, taille_max):
            coin = (x,y)
            j = 0
            compte = 0                                      # compteur de pixels noirs
            while compte == 0 and j < taille_max:
                i = 0
                while compte == 0 and i < taille_max:
                    if source.getpixel((x+i,y+j)) != 255:
                        compte += 1
                    i += 1
                j += 1
            if compte == 0:                                 # si que des pixels blanc
                coordonnees.append(coin)
        if len(coordonnees) == 0:                           # Une taille de carrée plus grande ne retourne rien
            return  taille_max-1, liste_a_retourner         # Je retourne la liste précédente, décrémenter de 1 à cause de mon passage sans rien trouver à taille_max+1
        else:
            liste_a_retourner = coordonnees                 # Je stocke l'état de coordonnees pour un éventuel return dans la boucle d'après
            taille_max += 1                                 # je passe à la taille à détecter suivante
            coordonnees = []


def pgcb_iter(source):
    """
    source - référence d'une image carrée (au format 'L') déjà importée à l'aide de PIL au format 'L'
            La "couleur" d'un pixel noir est 0, celle d'un pixel blanc est 255
    Sortie: list - tableau d'association entre chaque pixel de l'image et la longueur
            du côté du plus grand carré blanc qu'il permet de définir
    """
    largeur, hauteur = source.size
    # On initialise tous les pixels comme s'ils étaient noirs
    memo = [[0 for y in range(largeur)] for x in range(hauteur)]

    for x in range(largeur):            # parcours des abscisses
        for y in range(largeur):        # parcours des ordonnées
            couleur = source.getpixel( (x, y) )

            if couleur == 0:            # Test inutile par initialisation mais important à écrire
                                        # car il correspond au 1er cas de la relation de récurrence
                memo[y][x] = 0          # Transposition
            elif (x == 0) or (y == 0):
                memo[y][x] = 1
            else:
                memo[y][x] = 1 + min(memo[y][x-1], memo[y-1][x-1], memo[y-1][x])
    return memo

def recherche_pgcb_iter(source):
    """
    source - référence d'une image carrée (au format 'L') déjà importée à l'aide de PIL au format 'L'
            La "couleur" d'un pixel noir est 0, celle d'un pixel blanc est 255
    Sortie: tuple - taille du côté du (ou des) plus grand(s) carré(s) blanc(s) de cette image
            et liste des coordonnées des coins haut/gauche de ceux-ci
    """
    largeur, hauteur = source.size
    # Création du tableau d'association
    memo = pgcb_iter(source)

    taille_max = 0
    liste_coor = []
    for x in range(largeur):
        for y in range(hauteur):
            if (taille_max != 0) and memo[x][y] == taille_max:
                liste_coor.append((y, x))       # Transposition
            elif memo[x][y] > taille_max:
                taille_max = memo[x][y]
                liste_coor = [(y, x)]           # Transposition
    liste_coor = [(coor[0]-taille_max+1, coor[1]-taille_max+1) for coor in liste_coor]
    return (taille_max, liste_coor)
Une solution

Voici un exemple de résultats. On peut à nouveau remarquer que l'algorithme glouton est très rapide mais pas du tout fiable tandis que notre algorithme dynamique est très rapide en comparaison des algorithmes naïfs : 

Affichage des temps d'exécution pour trouver le plus grand carré blanc dans une image
===== Test des temps pour Image_100_40_test.png =====

(5, [(63, 11), (44, 72)])
Durée Boucle For : 1.2100694179534912  secs
(5, [(63, 11), (44, 72)])
Durée Boucle While : 0.24201393127441406  secs
(3, [(3, 2)])
Durée Glouton : 0.0009999275207519531  secs
(5, [(63, 11), (44, 72)])
Durée Dynamique Itératif : 0.021001100540161133  secs



===== Test des temps pour Image_200_30_test.png =====

(6, [(60, 86)])
Durée Boucle For : 7.8124470710754395  secs
(6, [(60, 86)])
Durée Boucle While : 1.3790786266326904  secs
(3, [(6, 2), (42, 2), (60, 2), (75, 2), (84, 2), (114, 2), (126, 2)])
Durée Glouton : 0.0009999275207519531  secs
(6, [(60, 86)])
Durée Dynamique Itératif : 0.08200478553771973  secs



===== Test des temps pour Image_300_40_test.png =====

(5, [(117, 84), (223, 194), (134, 230)])
Durée Boucle For : 11.509658336639404  secs
(5, [(117, 84), (223, 194), (134, 230)])
Durée Boucle While : 2.1801247596740723  secs
(3, [(42, 2)])
Durée Glouton : 0.002000093460083008  secs
(5, [(117, 84), (223, 194), (134, 230)])
Durée Dynamique Itératif : 0.18301033973693848  secs

Vous trouverez ci-dessous un exemple de programme permettant d'obtenir ces résultats : 

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
from PIL import Image
import time

# Fonctions

def recherche_pgcb_for(source):
    """
    source - référence d'une image carrée (au format 'L') déjà importée à l'aide de PIL au format 'L'
            La "couleur" d'un pixel noir est 0, celle d'un pixel blanc est 255
    Sortie: list - tableau d'association entre chaque pixel de l'image et la longueur
            du côté du plus grand carré blanc qu'il permet de définir
    """
    largeur, hauteur = source.size                          # L'image est carrée donc largeur = hauteur
    coordonnees = []
    taille_max = 1
    for taille_max in range(1, min(largeur, hauteur)):      # On cherche un carré. On aurait pu écrire largeur au lieu de min(largeur, hauteur)
        if taille_max == 1:                                 # La détection d'un carré de 1px de côté est plus simple
            for y in range(hauteur):
                for x in range(largeur):
                    if source.getpixel((x,y)) == 255:       # Si je trouve un blanc j'ajoute à la liste
                        coordonnees.append((x, y))

        else:                                               # Détection carré > 1px
            for y in range(hauteur - taille_max):
                for x in range(largeur - taille_max):
                    coin = (x,y)
                    compte = 0                              # compteur de pixels noirs
                    for j in range(0,taille_max):
                        for i in range(0,taille_max):
                            if source.getpixel((x+i,y+j)) != 255:   # si c'est différent d'un pixel blanc
                                compte += 1
                    if compte == 0:                                 # si que des pixels blanc
                        coordonnees.append(coin)

        if len(coordonnees) == 0:                           # Une taille de carrée plus grande ne retourne rien
            return taille_max-1, liste_a_retourner          # Je retourne la liste précédente, décrémenter de 1 à cause de mon passage sans rien trouver à taille_max+1
        else:
            liste_a_retourner = coordonnees                 # Je stocke l'état de coordonnees pour un éventuel return dans la boucle d'après
            taille_max += 1                                 # je passe à la taille à détecter suivante
            coordonnees = []                                # Je remets à zéro ma liste


def recherche_pgcb_while(source):
    """
    source - référence d'une image carrée (au format 'L') déjà importée à l'aide de PIL au format 'L'
            La "couleur" d'un pixel noir est 0, celle d'un pixel blanc est 255
    Sortie: list - tableau d'association entre chaque pixel de l'image et la longueur
            du côté du plus grand carré blanc qu'il permet de définir
    """
    largeur, hauteur = source.size                          # L'image est carrée donc largeur = hauteur
    coordonnees = []
    taille_max = 1
    for taille_max in range(1, min(largeur, hauteur)):      # On cherche un carré. On aurait pu écrire largeur au lieu de min(largeur, hauteur)
        if taille_max == 1:                                 # La détection d'un carré de 1px de côté est plus simple
            for y in range(hauteur):
                for x in range(largeur):
                    if source.getpixel((x,y)) == 255:       # Si je trouve un blanc j'ajoute à la liste
                        coordonnees.append((x, y))
        else:                                               # Détection carré > 1px
            for y in range(hauteur - taille_max):
                for x in range(largeur - taille_max):
                    coin = (x,y)
                    j = 0
                    compte = 0                              # compteur de pixels noirs
                    while compte == 0 and j < taille_max:
                        i = 0
                        while compte == 0 and i < taille_max:
                            if source.getpixel((x+i,y+j)) != 255:
                                compte += 1
                            i += 1
                        j += 1
                    if compte == 0:                         # si que des pixels blanc
                        coordonnees.append(coin)
        if len(coordonnees) == 0:                           # Une taille de carrée plus grande ne retourne rien
            return taille_max-1, liste_a_retourner          # Je retourne la liste précédente, décrémenter de 1 à cause de mon passage sans rien trouver à taille_max+1
        else:
            liste_a_retourner = coordonnees                 # Je stocke l'état de coordonnees pour un éventuel return dans la boucle d'après
            taille_max += 1                                 # je passe à la taille à détecter suivante
            coordonnees = []                                # Je remets à zéro ma liste


def recherche_pgcb_glouton(source):
    """
    source - référence d'une image carrée (au format 'L') déjà importée à l'aide de PIL au format 'L'
            La "couleur" d'un pixel noir est 0, celle d'un pixel blanc est 255
    Sortie: list - tableau d'association entre chaque pixel de l'image et la longueur
            du côté du plus grand carré blanc qu'il permet de définir
    """
    largeur, hauteur = source.size                          # L'image est carrée donc largeur = hauteur
    coordonnees = []
    taille_max = 1
    for y in range(0, hauteur - taille_max, taille_max):
        for x in range(0, largeur - taille_max, taille_max):
            coin = (x,y)
            j = 0
            compte = 0                                      # compteur de pixels noirs
            while compte == 0 and j < taille_max:
                i = 0
                while compte == 0 and i < taille_max:
                    if source.getpixel((x+i,y+j)) != 255:
                        compte += 1
                    i += 1
                j += 1
            if compte == 0:                                 # si que des pixels blanc
                coordonnees.append(coin)
        if len(coordonnees) == 0:                           # Une taille de carrée plus grande ne retourne rien
            return  taille_max-1, liste_a_retourner         # Je retourne la liste précédente, décrémenter de 1 à cause de mon passage sans rien trouver à taille_max+1
        else:
            liste_a_retourner = coordonnees                 # Je stocke l'état de coordonnees pour un éventuel return dans la boucle d'après
            taille_max += 1                                 # je passe à la taille à détecter suivante
            coordonnees = []


def pgcb_iter(source):
    """
    source - référence d'une image carrée (au format 'L') déjà importée à l'aide de PIL au format 'L'
            La "couleur" d'un pixel noir est 0, celle d'un pixel blanc est 255
    Sortie: list - tableau d'association entre chaque pixel de l'image et la longueur
            du côté du plus grand carré blanc qu'il permet de définir
    """
    largeur, hauteur = source.size
    # On initialise tous les pixels comme s'ils étaient noirs
    memo = [[0 for y in range(largeur)] for x in range(hauteur)]

    for x in range(largeur):            # parcours des abscisses
        for y in range(largeur):        # parcours des ordonnées
            couleur = source.getpixel( (x, y) )

            if couleur == 0:            # Test inutile par initialisation mais important à écrire
                                        # car il correspond au 1er cas de la relation de récurrence
                memo[y][x] = 0          # Transposition
            elif (x == 0) or (y == 0):
                memo[y][x] = 1
            else:
                memo[y][x] = 1 + min(memo[y][x-1], memo[y-1][x-1], memo[y-1][x])
    return memo

def recherche_pgcb_iter(source):
    """
    source - référence d'une image carrée (au format 'L') déjà importée à l'aide de PIL au format 'L'
            La "couleur" d'un pixel noir est 0, celle d'un pixel blanc est 255
    Sortie: tuple - taille du côté du (ou des) plus grand(s) carré(s) blanc(s) de cette image
            et liste des coordonnées des coins haut/gauche de ceux-ci
    """
    largeur, hauteur = source.size
    # Création du tableau d'association
    memo = pgcb_iter(source)

    taille_max = 0
    liste_coor = []
    for x in range(largeur):
        for y in range(hauteur):
            if (taille_max != 0) and memo[x][y] == taille_max:
                liste_coor.append((y, x))       # Transposition
            elif memo[x][y] > taille_max:
                taille_max = memo[x][y]
                liste_coor = [(y, x)]           # Transposition
    liste_coor = [(coor[0]-taille_max+1, coor[1]-taille_max+1) for coor in liste_coor]
    return (taille_max, liste_coor)



##############################
### Programme Principal ######
##############################

noms = ['Image_100_40_test.png', 'Image_200_30_test.png', 'Image_300_40_test.png']


print("Affichage des temps d'exécution pour trouver le plus grand carré blanc dans une image")
for nom_fichier in noms :
    print(f'===== Test des temps pour {nom_fichier} =====\n')
    source = Image.open(nom_fichier)

    start = time.time()
    print(recherche_pgcb_for(source))
    end = time.time()
    print(f"Durée Boucle For : {end - start}  secs")

    start = time.time()
    print(recherche_pgcb_while(source))
    end = time.time()
    print(f"Durée Boucle While : {end - start}  secs")

    start = time.time()
    print(recherche_pgcb_glouton(source))
    end = time.time()
    print(f"Durée Glouton : {end - start}  secs")

    start = time.time()
    print(recherche_pgcb_iter(source))
    end = time.time()
    print(f"Durée Dynamique Itératif : {end - start}  secs")

    print('\n\n')

Question n°4☘

Déterminez la complexité du code réalisé en programmation dynamique.

Une réponse

On désigne par n le nombre de pixels sur un côté de l'image. Puisque l'image est carrée, ses dimensions sont n\times n.

On appelle la fonction recherche_pgcb_iter().

  • Cette fonction appelle la fonction pgcb_iter(). Dans pgcb_iter(), chaque pixel de l'image est parcouru une fois et une seule afin de compléter le tableau memo. Les instructions incluses dans la double boucle for sont toutes élémentaires donc la complexité temporelle de cette fonction est en O(n^2).
  • Une fois cet appel terminé, on parcourt chaque élément du tableau memo une fois et une seule afin de rechercher le maximum de ce tableau. Or memo comporte n lignes et n colonnes et les instructions incluses dans la double boucle for sont toutes élémentaires donc on est à nouveau en présence d'une complexité en O(n^2).

Par conséquent, la complexité temporelle de la fonction recherche_pgcb_iter() est en O(n^2), ce qui est bien meilleur que la complexité des algorithmes naïf.

On peut aussi remarque que la complexité en mémoire est en O(n^2) : elle correspond à la taille du tableau de mémoïsation memo.

Question n°5 - Pour aller plus loin☘

Complétez le corps de la fonction suivante : 

1
2
3
4
5
def visualisation(source):
    """
    source - référence d'une image carrée (au format 'L') déjà importée à l'aide de PIL au format 'L'
    Sortie: Image source dans laquelle les plus grand carrés blanc sont coloriés... en gris
    """

Un premier exemple pour tester

Avec l'image ci-contre dont la version agrandie est : Exemple 01 agrandi

on obtient l'image dont la version agrandie est : Exemple 01 gris agrandi

Un second exemple pour tester

Avec l'image ci-contre dont la version agrandie est : Exemple 02 agrandi

on obtient l'image dont la version agrandie est : Exemple 02 gris agrandi

Une solution
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
def visualisation(source):
    """
    source - référence d'une image carrée (au format 'L') déjà importée à l'aide de PIL au format 'L'
    Sortie: Image source dans laquelle les plus grand carrés blanc sont coloriés... en gris
    """
    taille_max, liste_coor = recherche_pgcb_iter(source)
    for coor in liste_coor:
        for i in range(taille_max):
            for j in range(taille_max):
                source.putpixel( (coor[0]+i, coor[1]+j), 200)
    return source