Un soupçon de C☘

Ces exercices doivent être utilisés pour vous entraîner à comprendre/travailler avec un nouveau langage de programmation. Les questions sont accompagnés de leur solution pour vous permettre de progresser.
Cependant, il ne vous sera pas demandé de savoir coder en C cette année (ni l'année prochaine d'ailleurs).

Ne vous précipitez pas sur ces solutions dès la première difficulté, vous êtes capable de trouver par vous-mêmes.

Le langage C est un langage important créé au début des années 1970, fondamental dans les systèmes UNIX. De nombreux langages héritent, d'une façon ou d'une autre, de ce langage C.

Nous allons utiliser ce langage pour travailler sur la représentation des entiers relatifs en machine.

ExerciceA03.51 - Les entiers en C☘

En Python, les nombres entiers sont de type int et ... c'est tout ! Le langage gère « tout seul » la mémoire nécessaire pour travailler sur ces entiers.

En C, ils existent plusieurs types différents pour les entiers, selon la place en mémoire qu'ils vont occuper :

Type	Description	Taille en mémoire
`signed char`	Entier signé	1 octet
`unsigned char`	Entier positif	1 octet
`signed short`	Entier standard signé	2 octets
`unsigned short`	Entier standard positif	2 octets
`signed long`	Entier long signé	4 octets
`unsigned long`	Entier long positif	4 octets

Les entiers de type signed short ou unsigned short sont codés sur deux octets.

Combien d'entiers distincts peut-on coder sur deux octets ?

Une piste
Un octet (en anglais : byte) correspond à 8 bits.
Un bit peut prendre deux valeurs (0 ou 1).

Réponse
Sur deux octets, c'est à dire 16 bits, on dispose de $2^{16} = 65536$ codes différents. On peut donc a priori coder 65536 entiers sur ces deux octets.
Un entier de type signed short a une valeur comprise entre $-2^{15} = -32768$ et $2^{15}-1 = 32767$ .
A-t-on codé 65536 entiers distincts sur ces deux octets ?

Réponse
32768 entiers sont strictement négatifs et 32767 entiers sont strictement positifs. En prenant en compte 0, cela fait bien un total de 65536 entiers.

ProgA03.52 - Exécuter du C☘

Pour éviter d'avoir à installer sur vos machines le nécessaire pour compiler du C, on utilisera des compilateurs en ligne.

Par exemple:

Questions☘

Connectez-vous sur le site online_c_compiler.
Ce site s'ouvre sur un court exemple de programme. Testez-le.

Copiez/collez le code C ci-dessous dans le compilateur en ligne :

#include <stdio.h>

int main() {
    /* On déclare une variable x de type signed char
    puis on lui affecte la valeur 10. */
    signed char x = 10 ; 

    /* On déclare une variable y de type signed char
    puis on lui affecte la valeur 25. */
    signed char y = 25 ;

    /* On déclare une variable z de type signed char
    puis on lui affecte la valeur x+y. */
    signed char z = x + y ;

    /* On affiche le contenu de z : */
    printf("Somme x + y = %hd", z) ;
}

Anticipez le texte qui sera affiché à l'écran puis exécutez le code afin de confirmer votre réponse.
Réponse
On obtient, sans surprise :
```
Somme x + y = 35
```

Modifiez le code pour ajouter les nombres 112 et 25.
Anticipez le texte qui sera affiché à l'écran puis exécutez le code afin de confirmer votre réponse.

Réponse

On obtient, avec surprise :

Somme x + y = -119

En fait, ce n'est pas si surprenant si vous vous souvenez le travail réalisé sur le dépassement de capacité dans une plage de représentation binaire par complément à 2 sur un octet.

Rappel

retenues	1	1	1
	0	1	1	1	0	0
+	0	0	0	1	1	1
	1	0	0	0	1	1

Or $(1000 \; 1001)_2$ est la représentation binaire en complément à deux d'un entier négatif.

L'entier positif qui correspond à cette représentation binaire « usuelle » est $137$ .
On soustrait à cet entier $2^8$ : $137 - 256 = -119$ .
Dès lors, la somme de la représentation par complément à 2 sur un octet des entiers $112$ et $25$ donne $-119$ .

En effet, on a dépassé la valeur du plus grand entier représenté par complément à 2 sur un octet donc on a continué sur la « roue »

Remarque

On aurait pu s'attendre à un message d'erreur du type « dépassement de capacité ».
Sans un tel message, on voit que c'est au programmeur de gérer ce type de dépassement ce qui n'est pas sans poser problèmes (bugs...).

ProgA03.53 - `max+1 = min`☘

Connectez-vous sur le site online_c_compiler.

Copiez/collez le code C de l'exercice précédent puis modifiez ce code pour ajouter les nombres 127 et 1.

Réponse

Le code modifié (sans les commentaires) :

int main() {
    signed char x = 127;

    signed char y = 1;

    signed char z = x + y;

    printf("Somme x + y = %hd", z);
}

Anticipez le texte qui sera affiché à l'écran avant d'exécutez le code pour confirmer votre réponse.
Réponse
On obtient:
```
Somme x + y = -128
```
Vous avez bien vu : il y a un signe « - » devant le résultat !
Pouvait-on s'attendre au résultat obtenu ?

Réponse
Bien sûr !
Il y a un nouveau dépassement de capacité : l'entier relatif qui suit $127$ sur la roue dans une représentation par complément à 2 sur un octet est $-128$ .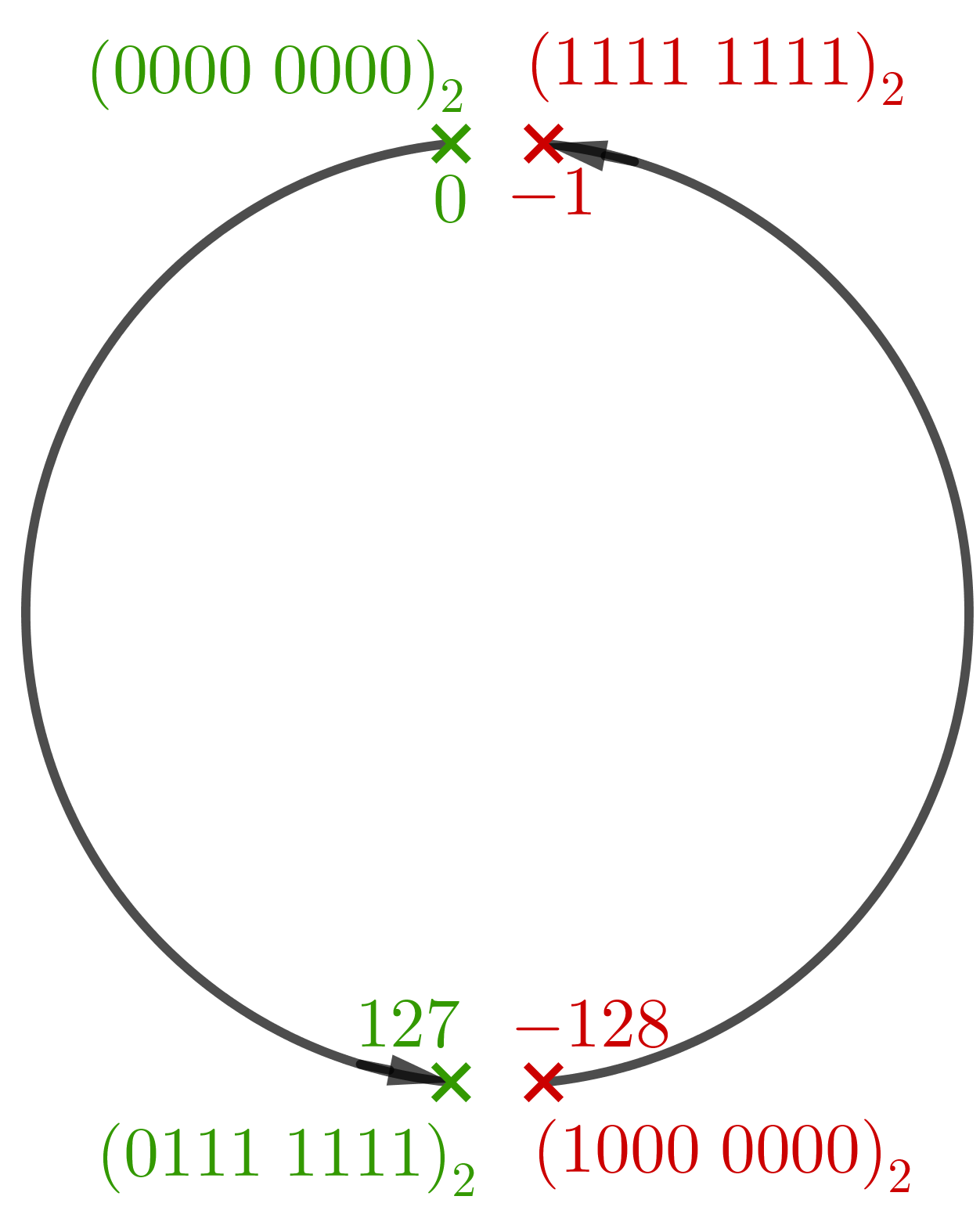

ProgA03.54 - Et sur deux octets ?☘

On rappelle que les signed short du langage C sont des entiers codés en complément à deux sur 16 bits.

Connectez-vous sur le site online_c_compiler.

Copiez/collez puis exécutez le code C ci-dessous dans le compilateur en ligne :

#include <stdio.h>

int main() {
    /* On déclare une variable x de type signed short
    puis on lui affecte la valeur 10. */
    signed short x = 10 ; 

    /* On déclare une variable y de type signed short
    puis on lui affecte la valeur 25. */
    signed short y = 25 ;

    /* On déclare une variable z de type signed short
    puis on lui affecte la valeur x+y. */
    signed short z = x + y ;

    /* On affiche le contenu de z : */
    printf("Somme x + y = %hd", z) ;
}

Modifiez le code pour ajouter les nombres 112 et 25.
Anticipez le texte qui sera affiché à l'écran puis exécutez le code afin de confirmer votre réponse.
Réponse
On obtient, sans surprise :
```
Somme x + y = 137
```
Modifiez le code pour ajouter les nombres 32767 et 1.
Anticipez le texte qui sera affiché à l'écran puis exécutez le code afin de confirmer votre réponse.
Réponse
On obtient :
```
Somme x + y = -32768
```
A nouveau, on a fait apparaître un dépassement de capacité !

Justifiez, sur le cahier, le résultat obtenu à la question précédente.

Réponse

Les entiers de types signed short sont compris entre $-2^{15} = -32768$ et $2^{15}-1 = 32767$ .

La représentation en complément à 2 sur 16 bits de 32767 est donc $(0111 \; 1111 \; 1111 \; 1111)_2$ .

La représentation de 1 est $(0000 \; 0000 `\; 0000 \; 0001)_2$ .

Effectuons la somme :

retenues	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
	0	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
+	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1
	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0

On obtient $(1000 \; 0000 \; 0000 \; 0000)_2$ .

Or $(1000 \; 0000 \; 0000 \; 0000)_2 = 2^{15} = 32768$ et l'entier maximal représenté en complément à deux sur 16 bit est 32767.

Puisque $32768 - 2^{16} = -32768$ , le code $(1000 \; 0000 \; 0000 \; 0000)_2$ est donc la représentation de l'entier $-32768$ .

Modifiez le code pour ajouter les nombres -11256 et -25343.
Anticipez le texte qui sera affiché à l'écran puis exécutez le code afin de confirmer votre réponse.
Réponse
On obtient :
```
Somme x + y = 28937
```
Justifiez ce résultat sur votre cahier.

Réponse
La somme (en base 10) de -11256 et -25343 donne -36599.

Or le plus petit entier représenté par complément à 2 sur deux octets est -32768. Il y a donc un dépassement de capacité.

Lorsqu'on prend « à rebours » la roue des représentations sur deux octets, le précédent de -32768 est 32767.

Puisque la différence entre -32768 et -36599 est 3831, il faut effectuer 3831 pas « à rebours » sur cette roue, soit 3830 pas depuis 32767.

Or $32767 - 3830 = 28937$ , ce qui confirme le résultat renvoyé par le programme rédigé en C.

Un soupçon de C☘

ExerciceA03.51 - Les entiers en C☘

ProgA03.52 - Exécuter du C☘

Questions☘

ProgA03.53 - max+1 = min☘

ProgA03.54 - Et sur deux octets ?☘

ProgA03.53 - `max+1 = min`☘