Complément à deux

Pour faciliter la manipulation, on explique le codage utilisé en machine pour représenter les entiers signés sur un octet (type signed char en langage C).

Représenter des entiers relatifs sur un octet

1. Combien d'entiers distincts peut-on coder sur 8 bits ?

   Une réponse

   On dispose de 2⁸ = 256 codes différents.

2. Si on décide de coder uniquement des entiers positifs :

   1. quel sera le plus petit entier codé ?
   2. quel sera le plus grand entier codé ?
   Une réponse

   On code les entiers de $(0000 \; 0000)_2 = 0$ à $(1111 \; 1111)_2 = 255$.

3. Si on décide de coder les entiers signés d'un intervalle [ e_min; e_max] comportant autant d'entiers strictement négatifs que d'entiers positifs ou nul :

   1. quelle sera la valeur de e_min ?
   2. quelle sera la valeur de e_max ?
   Une réponse

   Le plus petit sera -2⁷ = -128.
   Le plus grand sera 2⁷ - 1 = 127.

Comment sont-ils codés en machine ?

Pour représenter les entiers relatifs de $-128$ à $127$ sur un octet, le codage utilisé est le suivant :

• Les entiers positifs de $0$ à $127$ sont représentés en binaire « comme d'habitude » :

  • $(0000 \; 0000)_2$ représente $0$ ;
  • $(0000 \; 0001)_2$ représente $1$ ;
  • $(0000 \; 0010)_2$ représente $2$ ;
  • $(0000 \; 0011)_2$ représente $3$ ;
  • ... ;
  • $(0111 \; 1110)_2$ représente $126$ ;
  • $(0111 \; 1111)_2$ représente $127$ ;

• Les entiers négatifs de $-128$ à $-1$ sont obtenus par « complément à rebours » :

  A retenir

  Le nombre négatif $x$ a pour représentation binaire celle de l'entier positif $2^8 + x$.

  L'idée est la suivante : après la représentation $(0111 \; 1111)_2$ qui désigne $+127$ (le dernier positif), on repart à $-128$ qui est représenté par $(1000 \; 0000)_2$. Ainsi :

  • $(1000 \; 0000)_2$ représente $-128$ car $2^8-128 = 128$ ;
  • $(1000 \; 0001)_2$ représente $-127$ car $2^8-127 = 129$ ;
  • $(1000 \; 0010)_2$ représente $-126$ car $2^8-126 = 130$ ;
  • ... ;
  • $(1111 \; 1110)_2$ représente $-2$ car $2^8-2 = 254$ ;
  • $(1111 \; 1111)_2$ représente $-1$ car $2^8-1 = 255$ ;

Avantages

1. Les représentations binaires ayant un « 0 » à gauche désignent les positifs tandis que les représentations ayant un « 1 » à gauche désignent les négatifs.
2. On peut illustrer cette représentation par une « roue » :

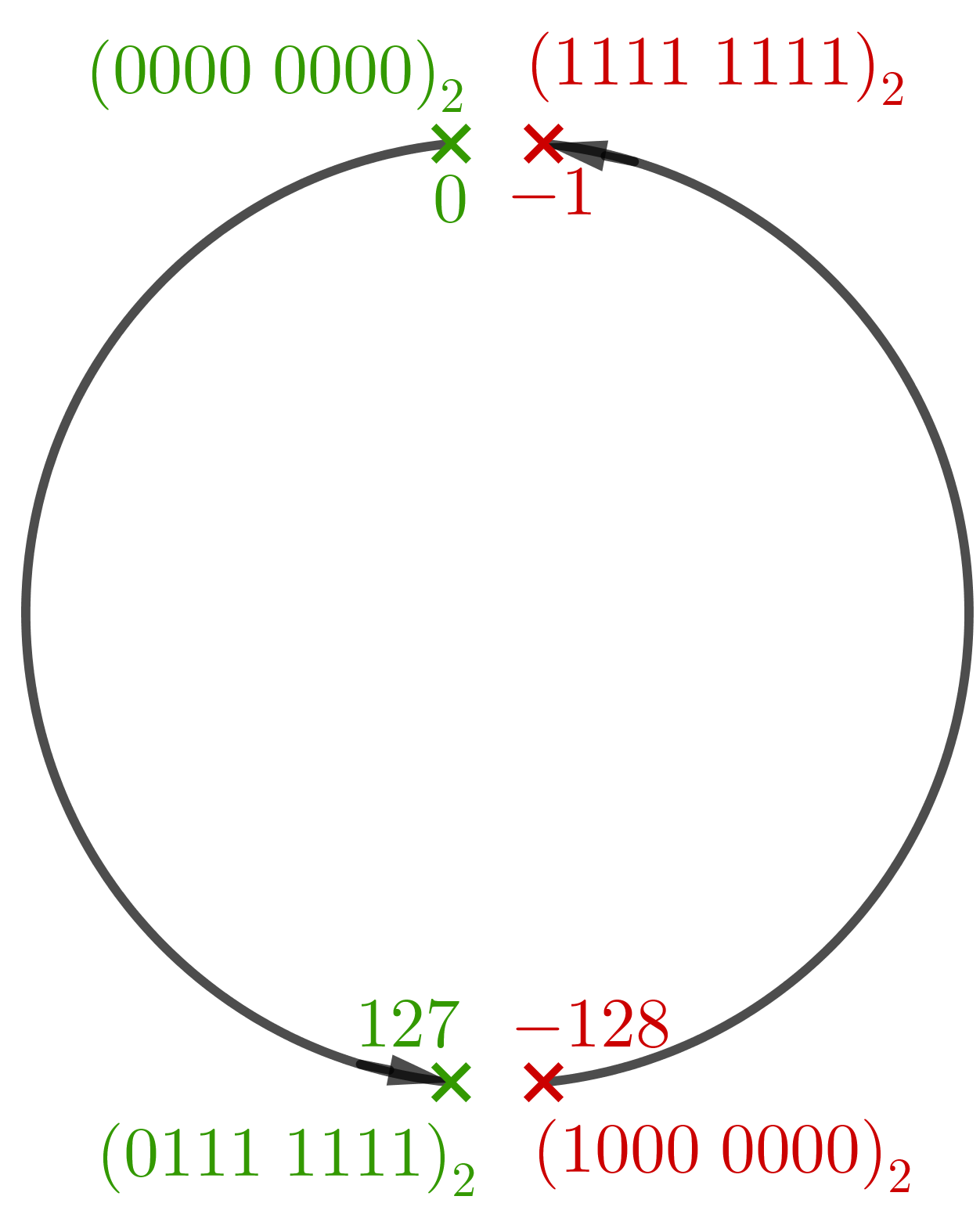
Utiliser ce graphique

On peut imaginer que l'on tourne sur un cercle :

• dans un sens, on compte les pas en positif ;
• dans l'autre sens on les compte en négatif.

En complément à 2 sur 8 bits, on découpe en $2^8 = 256$ arcs de même longueur :

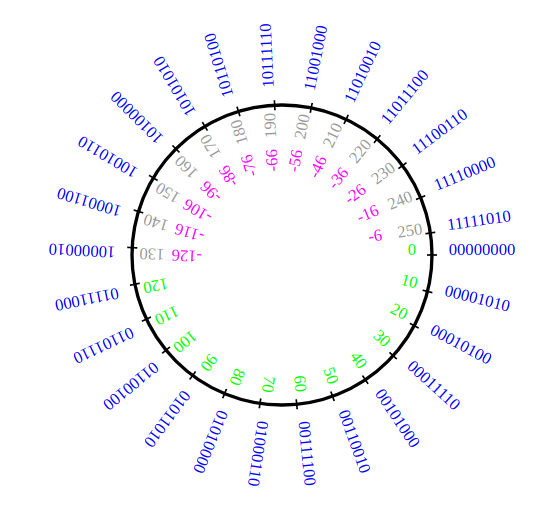
Cette image montre que $-1$ va correspondre avec $255$ et sera donc représenté par l'écriture binaire de $255$.

Si on pense « en tour », on observe qu'il faut un tour complet pour passer de $-1$ à $255$ : il faut donc ajouter $256 = 2^8$ à $-1$ pour obtenir l'entier positif donnant le code de $-1$.

De même, si l'on fait un tour complet dans le sens positif à partir de $-6$, on tombe sur $250$. C'est donc l'écriture binaire de $250$ qui donne la représentation par complément à 2 sur 8 bits de $-6$.

Important

L’octet $(1001 1100)_2$ représente $156$ dans le codage binaire des entiers positifs.
L’octet $(1001 1100)_2$ représente $–100$ dans le codage par complément à 2 des entiers relatifs.

Un même code binaire peut donc représenter deux entiers distincts !

Il est impératif de savoir de quel codage il s'agit !

En langage C, la valeur d'une variable de type signed short (entier signé sur 2 octets) sera codée en complément à deux sur 16 bits, tandis que la valeur d'une variable de type unsigned short (entier positif sur 2 octets) sera codée par son écriture usuelle en base deux.
C'est le type de la variable (indiqué par le programmeur en langage C) qui permet de savoir si le code doit être lu comme un code « complément deux » ou comme un code « écriture binaire usuelle ».