Somme de deux entiers sur un octet

Le choix de la représentation en complément à deux a été motivé par ses avantages lors de l'addition de deux entiers avec cette écriture.

Voyons quelques exemples sur un octet.

Somme de 37 et 22.

1. Donner le code binaire de 37 et le code binaire de 22 en complément à deux sur 8 bits.

   Réponse

   37 et 22 sont des entiers positifs, ils sont codés par leur écriture binaire usuelle.

   37 est représenté par $(0010 \; 0101)_2$.

   22 est représenté par $(0001 \; 0110)_2$.

2. Additionner 37 et 22 à l'aide de ces codes.
   Donner l'entier décimal correspondant.

   Réponse

   On effectue la somme comme appris à l'école élémentaire (mais en base deux) :

   retenues					1
   	0	0	1	0	0	1	0	1
   +	0	0	0	1	0	1	1	0
   	0	0	1	1	1	0	1	1

   Et $(0011 \; 1011)_2$ représente $(59)_{10}$.

Somme de 40 et -20.

1. Donner le code binaire de 40 et le code binaire de -20 en complément à deux sur 8 bits.

   Réponse

   40 est un entier positif, il est représenté par son écriture binaire usuelle : $(0010 \; 1000)_2$.

   -20 est négatif. Son code binaire par complément à 2 est donné par l'écriture binaire de $-20 + 2^8 = 236$.
   Or $(236)_{10}$ est représenté usuellement par $(1110 \; 1100)_2$.

   Le code en complément à 2 sur 8 bits de -20 est donc $(1110 \; 1100)_2$.

2. Additionner 40 et -20 à l'aide de ces codes.
   Donner l'entier décimal correspondant.

   Réponse

   Les représentations n'étant pas les codes binaires usuels, il n'y a aucune raison pour qu'une addition binaire usuelle donne le bon résultat.

   Toutefois, l'une des raisons du choix de la représentation des entiers relatifs en complément à deux est qu'elle préserve un algorithme d'addition très simple. Il suffit d'additionner (au sens usuel en binaire) les deux représentations pour obtenir le résultat :

   retenues	1	1	1		1
   		0	0	1	0	1	0	0	0
   +		1	1	1	0	1	1	0	0
   	1	0	0	0	1	0	1	0	0

   Comme la représentation est sur 8 bits, le « 1 » à gauche généré par une retenue disparaît et le code binaire restant sur un octet est $(0001 \; 0100)_2$.

   Or $(0001 \; 0100)_2$ est la représentation binaire en complément à deux de l'entier $2^4 + 2^2 = 20$, c'est-à-dire $40-20$.

Somme de -90 et -20.

Vérifier de même que la somme de $-90$ et $-20$ peut s'effectuer par une simple addition binaire sur les codes de ces deux entiers en complément à deux.

Solution

On a vu que -20 est représenté en complément à deux (sur 8 bits) par $(1110 \; 1100)_2$.

$-90 + 2^8 = 166 = (1010 \; 0110)_2$.
Le code en complément à deux de $-90$ sur 8 bits est $(1010 \; 0110)_2$.

L'addition :

retenues	1	1	1		1	1
		1	0	1	0	0	1	1	0
+		1	1	1	0	1	1	0	0
	1	1	0	0	1	0	0	1	0

Le résultat est donc $(1001 \; 0010)_2$ puisque le 1 à gauche généré par la retenue n'est pas conservé sur 8 bits.

Pour retrouver l'entier négatif représenté par $(1001 \; 0010)_2$, on peut appliquer, à rebours, l'algorithme présenté dans la page précédente :

1. On enlève 1 : $(1001 \; 0001)_2$
2. On inverse tous les bits : $(0110 \; 1110)_2$
3. On lit la valeur absolue de l'entier relatif : 64+32+8+4+2 = 110
4. On en déduit que $(1001 \; 0010)_2$ représente l'entier $-110$ par complément à 2 sur un octet.

Vérification décimale : on a bien $-90 -20 = -110$.

Dépassement de capacité

On considère les entiers $87$ et $62$.

1. Déterminez leur représentation binaire par complément à 2 sur un octet.

   Réponse

   87 et 62 sont des entiers positifs, ils sont codés par leur écriture binaire usuelle.

   87 est codé par $(0101 \; 0111)_2$.

   62 est codé par $(0011 \; 1110)_2$.

2. La somme de ces représentations binaires est-elle la représentation par complément à 2 sur un octet de $149$ ? Justifier.

   Réponse

   retenues		1	1	1	1	1	1
   		0	1	0	1	0	1	1	1
   +		0	0	1	1	1	1	1	0
   		1	0	0	1	0	1	0	1

   Or $(1001 \; 0101)_2$ est la représentation binaire en complément à deux d'un entier négatif.

   1. L'entier positif qui correspond à cette représentation binaire « usuelle » est $149$.
   2. On soustrait à cet entier $2^8$ : $149 - 256 = -107$.
   3. Dès lors, la somme de la représentation par complément à 2 sur un octet des entiers $87$ et $62$ donne $-107$.

   En effet, on a dépassé la valeur du plus grand entier représenté par complément à 2 sur un octet donc on a continué sur la « roue » :

   

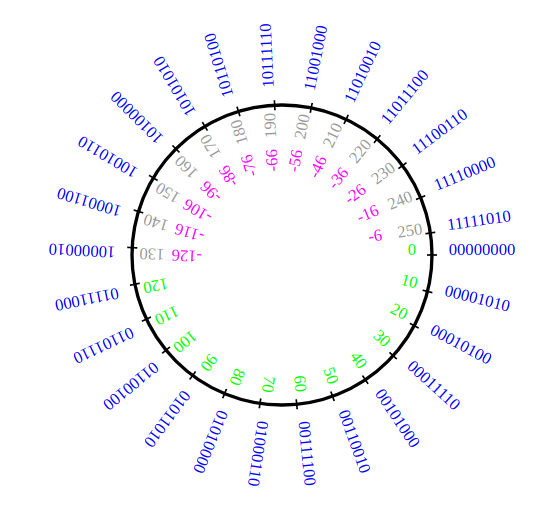
Important

La représentation par complément à 2 permet de conserver l'algorithme usuel d'addition sur la plage de représentation de ces entiers signés.

Lorsque le calcul renvoie un entier qui « sort » de cette plage de représentation, on poursuit le tour de la roue (dans un sens ou dans l'autre) :

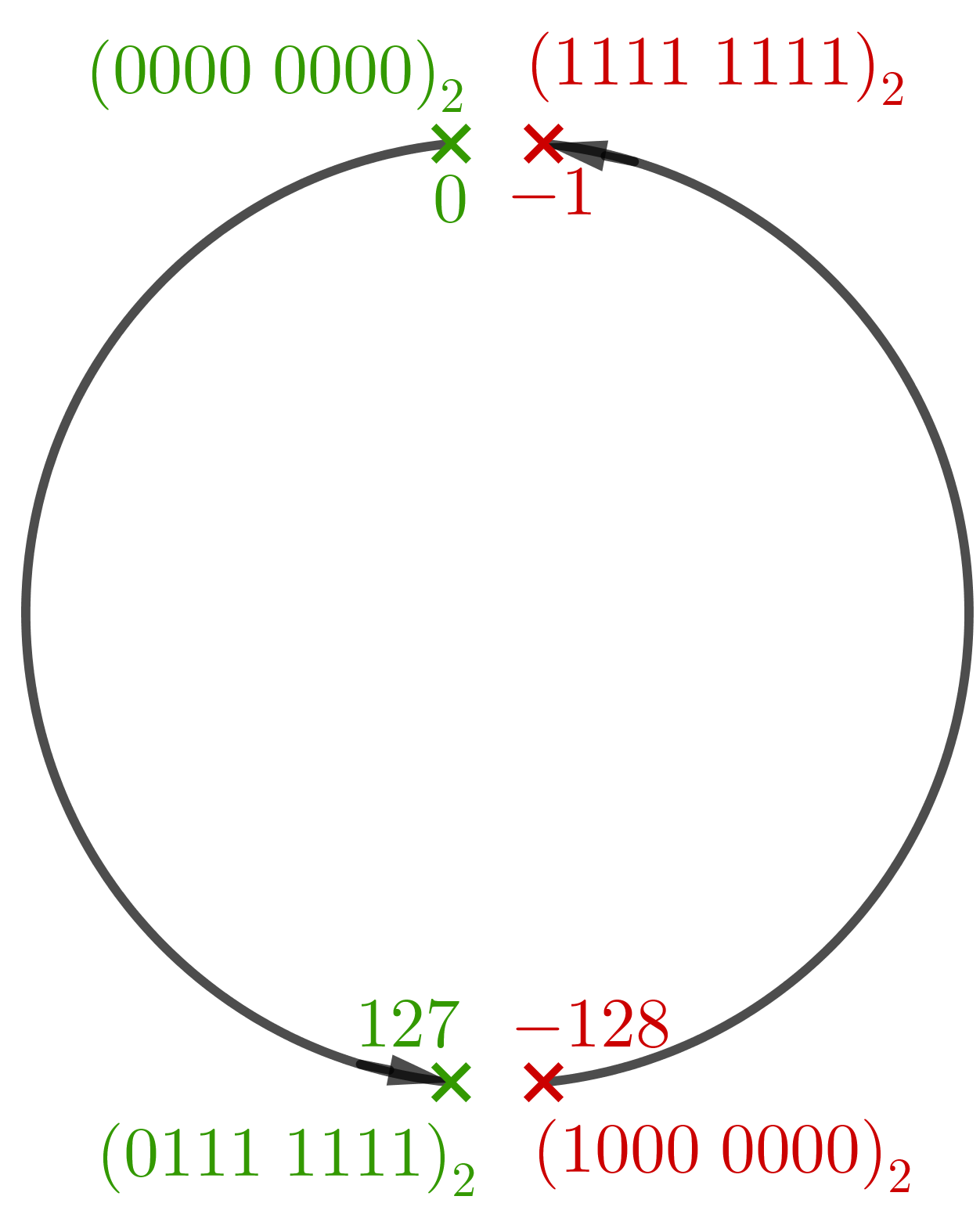
Un peu de culture générale

Ce type de dépassement est fréquent dans les appareils et services numériques, même les plus utilisés.

• Les GPS : tapez "bug du 6 avril 2019" dans un moteur de recherche.

• Youtube : Vous pouvez lire cet article tiré du journal Libération