Sujet n°35
Sujet original
Pour télécharger l'énoncé original, cliquer ici.
Exercice n°1
L'opérateur « ou exclusif » entre deux bits renvoie 0 si les deux bits sont
égaux et 1 s'ils sont différents. Il est symbolisé par le caractère ⊕.
Ainsi :
- 0 ⊕ 0 = 0
- 0 ⊕ 1 = 1
- 1 ⊕ 0 = 1
- 1 ⊕ 1 = 0
On représente ici une suite de bits par un tableau contenant des 0 et des 1.
Exemples
a = [1, 0, 1, 0, 1, 1, 0, 1]
b = [0, 1, 1, 1, 0, 1, 0, 0]
c = [1, 1, 0, 1]
d = [0, 0, 1, 1]
Écrire la fonction ou_exclusif qui prend en paramètres deux tableaux de même
longueur et qui renvoie un tableau où l’élément situé à position i est le
résultat, par l’opérateur « ou exclusif », des éléments à la position i des
tableaux passés en paramètres.
En considérant les quatre exemples ci-dessus, cette fonction doit passer les
tests suivants :
Exemples
>>> ou_exclusif(a, b)
[1, 1, 0, 1, 1, 0, 0, 1]
>>> ou_exclusif(c, d)
[1, 1, 1, 0]
Commentaires
La table de vérité aurait pu être présentée dans un tableau pour plus
de lisibilité
Une solution
Dans cette solution, on ajoute une assertion pour vérifier que les deux
tableaux ont la même longueur.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31 | def ou_exclusif(bits_a, bits_b):
"""
bits_a, bits_b - list, tableaux de bits de même longueur
Sortie: list - tableau de bits construit bit à bit en appliquant
l'opérateur xor entre les bits correspondants de bits_a et bits_b
"""
assert len(bits_a) == len(bits_b), "Les tableaux n'ont pas le même nombre de bits"
result = []
for i in range(len(bits_a)):
if bits_a[i] == bits_b[i]:
result.append(0)
else:
result.append(1)
return result
if __name__ == '__main__':
# Exemples de l'énoncé
a = [1, 0, 1, 0, 1, 1, 0, 1]
b = [0, 1, 1, 1, 0, 1, 0, 0]
c = [1, 1, 0, 1]
d = [0, 0, 1, 1]
print(ou_exclusif(a, b) == [1, 1, 0, 1, 1, 0, 0, 1])
print(ou_exclusif(c, d) == [1, 1, 1, 0])
# Exemples supplémentaires
print(ou_exclusif([0], [0]) == [0])
print(ou_exclusif([0], [1]) == [1])
print(ou_exclusif([1], [0]) == [1])
print(ou_exclusif([1], [1]) == [0])
|
Exercice n°2
Dans cet exercice, on appelle carré d’ordre n un tableau de n lignes et
n colonnes dont chaque case contient un entier naturel.
Exemples
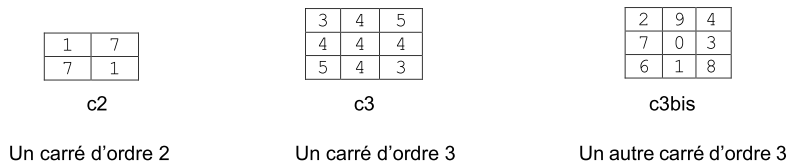
Un carré est dit semimagique lorsque les sommes des éléments situés sur chaque
ligne et chaque colonne sont égales.
- Ainsi c2 et c3 sont semimagiques car la somme de chaque ligne et chaque colonne
est égale à 8 pour c2 et 12 pour c3.
- Le carré c3bis n’est pas semimagique car la somme de la première ligne est égale
à 15 alors que celle de la deuxième ligne est égale à 10.
La classe Carre ci-après contient des méthodes qui permettent de manipuler
des carrés :
- La méthode constructeur crée un carré sous forme d’un tableau à deux dimensions
à partir d’une liste d’entiers, et d’un ordre.
- La méthode
affiche permet d’afficher le carré créé.
Exemples
>>> liste = (3, 4, 5, 4, 4, 4, 5, 4, 3)
>>> c3 = Carre(liste, 3)
>>> c3.affiche()
[3, 4, 5]
[4, 4, 4]
[5, 4, 3]
Compléter la méthode est_semimagique qui renvoie True si le carré est semimagique, False sinon.
Puis tester la fonction est_semimagique sur les carrés c2, c3 et c3bis.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39 | class Carre:
def __init__(self, liste, n):
self.ordre = n
self.tableau = [[liste[i + j * n] for i in range(n)] for
j in range(n)]
def affiche(self):
'''Affiche un carré'''
for i in range(self.ordre):
print(self.tableau[i])
def somme_ligne(self, i):
'''Calcule la somme des valeurs de la ligne i'''
somme = 0
for j in range(self.ordre):
somme = somme + self.tableau[i][j]
return somme
def somme_col(self, j):
'''Calcule la somme des valeurs de la colonne j'''
somme = 0
for i in range(self.ordre):
somme = somme + self.tableau[i][j]
return somme
def est_semimagique(self):
s = self.somme_ligne(0)
#test de la somme de chaque ligne
for i in range(...):
if ... != s:
return ...
#test de la somme de chaque colonne
for j in range(...):
if ... != s:
return ...
return ...
|
Tester la fonction est_magique sur les carrés c2, c3 et c4.
Commentaires sur le code original
Pour télécharger l'original du fichier à compléter,
cliquer ici.
Une solution
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59 | class Carre:
def __init__(self, liste, n):
self.ordre = n
self.tableau = [[liste[i + j * n] for i in range(n)] for
j in range(n)]
def affiche(self):
'''Affiche un carré'''
for i in range(self.ordre):
print(self.tableau[i])
def somme_ligne(self, i):
'''Calcule la somme des valeurs de la ligne i'''
somme = 0
for j in range(self.ordre):
somme = somme + self.tableau[i][j]
return somme
def somme_col(self, j):
'''Calcule la somme des valeurs de la colonne j'''
somme = 0
for i in range(self.ordre):
somme = somme + self.tableau[i][j]
return somme
def est_semimagique(self):
s = self.somme_ligne(0)
#test de la somme de chaque ligne
for i in range(1, self.ordre):
if self.somme_ligne(i) != s:
return False
#test de la somme de chaque colonne
for j in range(self.ordre):
if self.somme_col(j) != s:
return False
return True
if __name__ == '__main__':
# Exemple de l'énoncé
liste = (3, 4, 5, 4, 4, 4, 5, 4, 3)
c3 = Carre(liste, 3)
print(c3.est_semimagique() == True)
# Exemples supplémentaires
liste = (1, 7, 7, 1)
c2 = Carre(liste, 2)
print(c2.est_semimagique() == True)
liste = (2, 9, 4, 7, 0, 3, 6, 1, 8)
c3bis = Carre(liste, 3)
print(c3bis.est_semimagique() == False)
liste = (4, 5, 16, 9, 14, 7, 2, 11, 3, 10, 15, 6, 13, 12, 8, 1)
c4 = Carre(liste, 4)
print(c4.est_semimagique() == False)
|
