Aller au contenu

TP - Fractales☘

Dans le dossier [NSI], créez le dossier [D03-Recursivite].
Dans ce dossier, enregistrez vos fichiers avec le nom donné à l'exercice (TPD03.11.py, TPD03.12.py, ...).

Important

  1. Dans chaque fonction à programmer, remplacez le mot-clef pass par les instructions nécessaires.
  2. Pour gagner du temps, on ne lèvera pas les erreurs sur les types de données entrées par l'utilisateur. On considèrera que si la spécification indique un type int, alors ce sera bien un type int qui sera saisi.

Les TP avec une étoile peuvent être traités dans un deuxième temps...

TPD03.11 - La courbe de Von Koch☘

Ce premier TP a pour but de vous faire tracer une fractale appelée courbe de Von Koch.

Téléchargez le fichier « à trous » TPD03.11.py (clic droit -> [Enregistrer sous]) et enregistrez-le dans le dossier [D03-Recursivite].

Le processus de base☘

On part d'un segment (étape 0) :

puis on transforme ce segment ainsi (étape 1) :

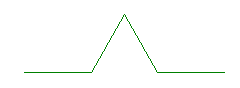
Dans cette figure transformée, chaque segment a une longueur égale au tiers de la longueur du segment de l'étape 0 et la base de la pointe a aussi cette longueur (on a donc un triangle équilatéral).

Complétez le code de la fonction etape(). Vous utiliserez uniquement les instructions left(), right() et forward().

1
2
3
4
5
6
7
def etape(stylo, cote):
    """
    stylo - une tortue
    cote - int, entier strictement positif, longueur du segment initial
    Sortie: None - La tortue trace une étape du flocon de VonKoch
    """
    pass

Testez ensuite cette fonction en effectuant un appel dans le Programme principal.

Conseil

Réalisez un dessin à la main avant de vous lancer dans la programmation pour bien identifier les angles de rotation.

La répétition☘

On réitère ensuite le processus précédent.

  • Etape 2 :
  • Etape 3 :
  • ...

En vous inspirant du travail réalisé dans la question précédente, complétez le code de la fonction récursive courbeVonKoch() qui permet de réaliser ces figures.
Attention, il ne faut pas faire appel à la fonction etape(), il faut s'inspirer de sa structure. 

1
2
3
4
5
6
7
8
def courbeVonKoch(stylo, n, cote):
    """
    stylo - une tortue
    n - int, nombre d'étapes à réaliser
    cote - int, entier strictement positif, longueur du segment initial
    Sortie: None - La tortue trace n étapes de la courbe  de VonKoch
    """
    pass
Une piste

Exprimer courbeVonKoch(stylo, n, cote) en fonction de courbeVonKoch(stylo, n-1, cote//3) :

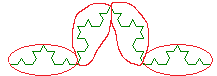
Exemple d'appel

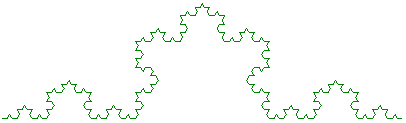
L'appel courbeVonKoch(sophie, 4, 400) permet de tracer l'image ci-dessous :

On change l'étape de base☘

On part d'un segment :

et maintenant on le tranforme comme suit :

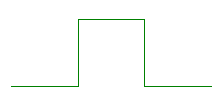
Proposez un code de répétition de ce processus comme vous l'avez fait pour la courbe de Von Koch.

1
2
3
4
5
6
7
8
def courbeCarreeVonKoch(stylo, n, cote):
    """
    stylo - une tortue
    n - int, nombre d'étapes à réaliser
    cote - int, entier strictement positif, longueur du segment initial
    Sortie: None - La tortue trace n étapes de la courbe  "carrée" de VonKoch
    """
    pass

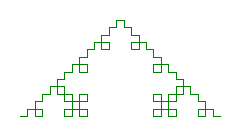
Exemple d'appel

L'appel courbeCarreeVonKoch(sophie, 3, 200) permet de tracer l'image ci-dessous :

TPD03.12 - Le triangle de Sierpinsky☘

Ce deuxième TP a pour but de vous faire tracer une fractale appelée triangle de Sierpinsky.

Téléchargez le fichier « à trous » TPD03.12.py (clic droit -> [Enregistrer sous]) et enregistrez-le dans le dossier [D03-Recursivite].

Le processus de base☘

Le triangle de Sierpinski est défini de la manière suivante :

  • On part d'un triangle équilatéral colorié (étape 0) :

  • puis on enlève le triangle central (étape 1) : Dans cette figure transformée, l'aire coloriée vaut trois fois l'aire non coloriée.

  • Complétez le code de la fonction dessine_triangle() qui trace un triangle équilatéral de longueur de côté cote. 

    3
4
5
6
7
8
9
    def dessine_triangle(stylo, cote):
    """
    stylo - une tortue
    cote, int, entier strictement positif, longueur d'un côté du triangle
    Sortie: None - La tortue trace un triangle équilatéral de longueur de côté cote
    """
    pass

  • Complétez la définition de la fonction etape() qui permet de représenter la figure de l'étape n°1. 

    12
13
14
15
16
17
18
    def etape(stylo, cote):
    """
    stylo - une tortue
    cote - int, entier strictement positif, longueur du segment initial
    Sortie: None - La tortue trace une étape du triangle de Sierpinsky
    """
    pass

La répétition☘

On réitère ensuite le processus précédent.

  • Etape 2 :

  • Etape 3 :

  • etc...

En vous inspirant du travail réalisé dans la question précédente, complétez la définition récursive de la fonction Sierpinski() qui permet de réaliser ces figures.
Attention, il ne faut pas faire appel à la fonction etape(), il faut s'inspirer de sa structure. 

21
22
23
24
25
26
27
28
def courbeVonKoch(stylo, n, cote):
    """
    stylo - une tortue
    n - int, nombre d'étapes à réaliser
    cote - int, entier strictement positif, longueur du segment initial
    Sortie: None - La tortue trace n étapes de la courbe  de VonKoch
    """
    pass

Exemple d'appel

L'appel Sierpinski(sophie, 4, 400) permet de tracer l'image ci-dessous :

TPD01.53 - La courbe du dragon☘

Auteurs

L'idée originale de ce TP provient de Messieurs LACPATIA, RUEL et SOLEILLANT, enseignants de l'académie de Lyon.

Ce dernier TP a pour but de vous faire tracer une fractale appelée courbe du Dragon.

Téléchargez le fichier « à trous » TPD03.13.py (clic droit -> [Enregistrer sous]) et enregistrez-le dans le dossier [D03-Recursivite].

Toutefois, il faut commencer par répondre à quelques questions sur son cahier...

Présentation de cette courbe☘

  • On plie une bande de papier en deux, et on la déplie, le motif obtenu est le suivant :

  • On plie une bande de papier en deux, puis à nouveau en deux (dans le même sens, arbitrairement à gauche), et on la déplie, le motif obtenu est le suivant :

  • On plie une bande de papier en deux, puis à nouveau en deux (dans le même sens, arbitrairement à gauche) et encore une troisième fois en deux, et on la déplie, le motif obtenu est le suivant :

  • On répète les pliages 4 fois de suite, on déplie la figure, on obtient le motif suivant :

  • On répète les pliages 5 fois, toujours dans le même sens et ensuite on déplie la bande de papier, on obtient le motif suivant :

Nous sommes rapidement limités au moment du 6ème ou du 7ème pliage alors même qu'il est possible d'appréhender la suite des figures ainsi obtenues :

Modélisation de la situation☘

On cherche à connaitre les différents pliages, quel que soit le numéro de l'étape, afin de pouvoir tracer le motif dessiné au bout d'un grand nombre d'itérations.

  • A l'étape 1, à l'issue du dépliage, on obtient un « coude » orienté vers la droite.
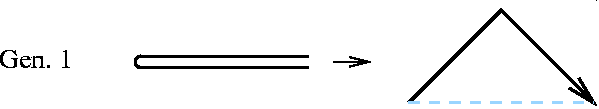    La figure ainsi obtenue sera notée D.

  • A l'étape 2, à l'issue du dépliage, on obtient trois « coudes » orientés successivement vers la droite, encore vers la droite puis vers la gauche.
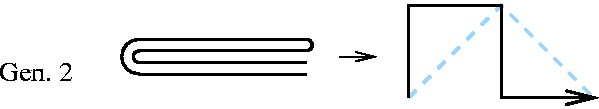    La figure ainsi obtenue sera notée D - D - G

  • A l'étape 3, à l'issue du dépliage, on obtient sept « coudes ».
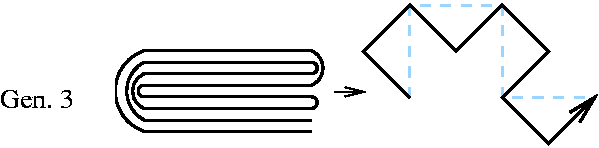    La figure ainsi obtenue sera noté D - D - G - D - D - G - G

  • etc...

Cette partie a pour but d'identifier comment passer d'une étape à la suivante à partir de ces modélisations. On peut déjà constater que le nombre de lettres est impaire dans chaque notation.

  1. Quelle est la lettre « centrale » dans chaque notation ? Pourquoi ?

  2. On a réécrit ci-contre la notation de l'étape 2 : , et celle de l'étape 3 : .
    A l'aide des indications de couleur, essayez d'identifier ce que sera la notation de l'étape 4.

  3. En déduire l'algorithme permettant de passer d'une étape à l'autre.

  4. Appelez l'enseignant pour vérifier vos réponses.

Programmation et visualisation☘

  1. Complétez la définition de la fonction inverse() qui prend comme argument une chaine de caractères constituée de 'D' et de 'G' et qui renvoie une chaine de caractères de même longueur dans laquelle les 'D' et les 'G' ont été échangés par rapport à la chaine initiale. De plus, cette deuxième chaîne est « renversée » par rapport à la première.

    3
4
5
6
7
8
9
    def inverse(chaine):
    """
    chaine - str, chaîne de caractères constituée de D et de G
    Sortie: str, chaîne de caractères de même longueur dans laquelle les D sont devenus des G
            et vice-versa, et l'ordre des lettres a été renversé
    """
    pass

    Exemple de tests

    >>> inverse('DDGDDGG')
'DDGGDGG'

>>> inverse('DDGDDGGDDDGGDGG')
'DDGDDGGGDDGGDGG'

  2. Complétez la définition récursive de la fonction dragon() qui renvoie la notation de la n-ième étape sous la forme d'une chaîne de caractères constituée de 'D' et de 'G'.

    13
14
15
16
17
18
    def dragon(n):
    """
    n - int, entier strictement positif
    Sortie: str, chaîne de caractères constituée de D et de G correspondant à la suite des pliages à l'étape n
    """
    pass

    Exemple de tests

    >>> dragon(1)
'D'

>>> dragon(3)
'DDGDDGG'

>>> dragon(6)
'DDGDDGGDDDGGDGGDDDGDDGGGDDGGDGGDDDGDDGGDDDGGDGGGDDGDDGGGDDGGDGG'

  3. En déduire la définition de la fonction dessin() qui permet de tracer la courbe du dragon avec turtle à l'étape n.

    22
23
24
25
26
27
28
    def dessin(stylo, n, dist):
    """
    stylo, une tortue
    n, dist - int, entiers strictement positifs
    Sortie: None, la tortue trace l'étape n de la courbe du dragon, avec des segments de longueur dist
    """
    pass

    Exemple

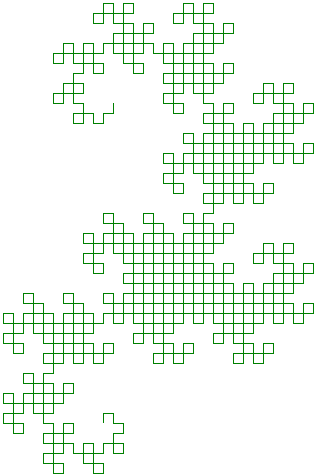
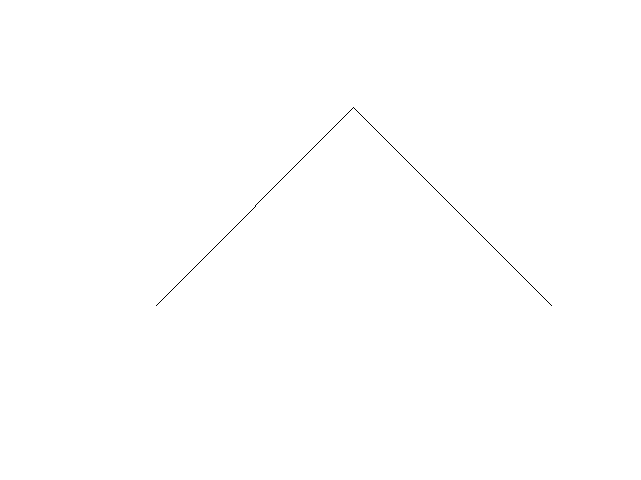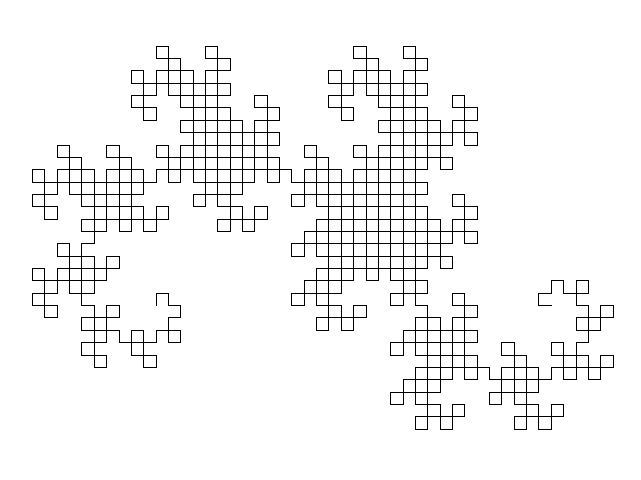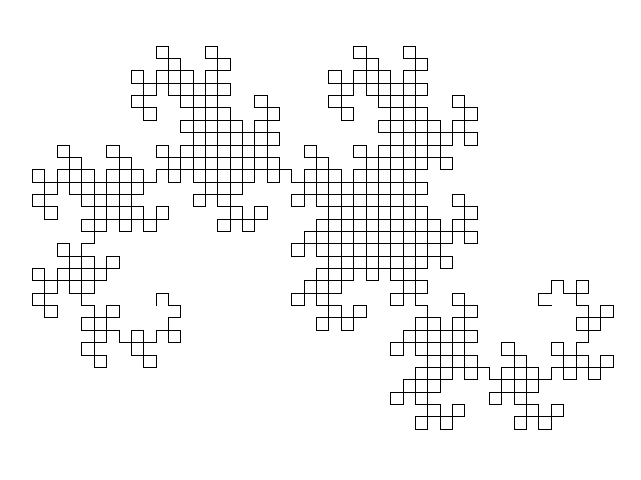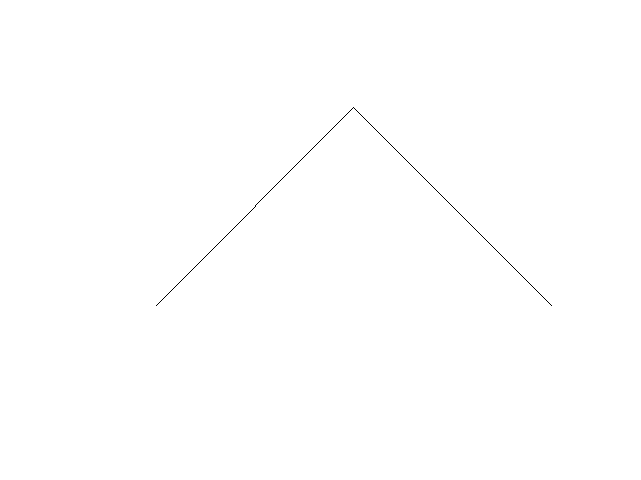
    L'appel dessin(sophie, 10, 10) renvoie la figure suivante :