Aller au contenu

Pile d'appels☘

Pour illustrer les exemples de cette partie, nous allons utiliser la fonction rectangle() définie comme suit :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
from turtle import *

def rectangle(n):
    """
    n - int, entier strictement positif
    """
    color('white', 'blue')
    begin_fill()
    for _ in range(2):
        forward(10)
        left(90)
        forward(n)
        left(90)
    end_fill()
    forward(10)


if __name__ == "__main__":
    TurtleScreen._RUNNING = True
    hideturtle()
    speed(0)
    rectangle(50)
    exitonclick()

Ordre des appels récursifs☘

Dans une fonction récursive, l'ordre d'exécution des instructions dépend des appels récursifs à la fonction. En d'autres termes, certaines instructions peuvent être exécutées immédiatement tandis que d'autres sont « mises en attente » dans une pile d'appels.

Un premier exemple☘

On considère la fonction récursive suivante :

17
18
19
20
21
22
23
def fct1(n):
    """
    n - int
    """
    if n > 10:
        rectangle(n)
        fct1(n-10)

On effectue l'appel fct1(50). Complétez la pile d'appel puis tracez la figure correspondante.

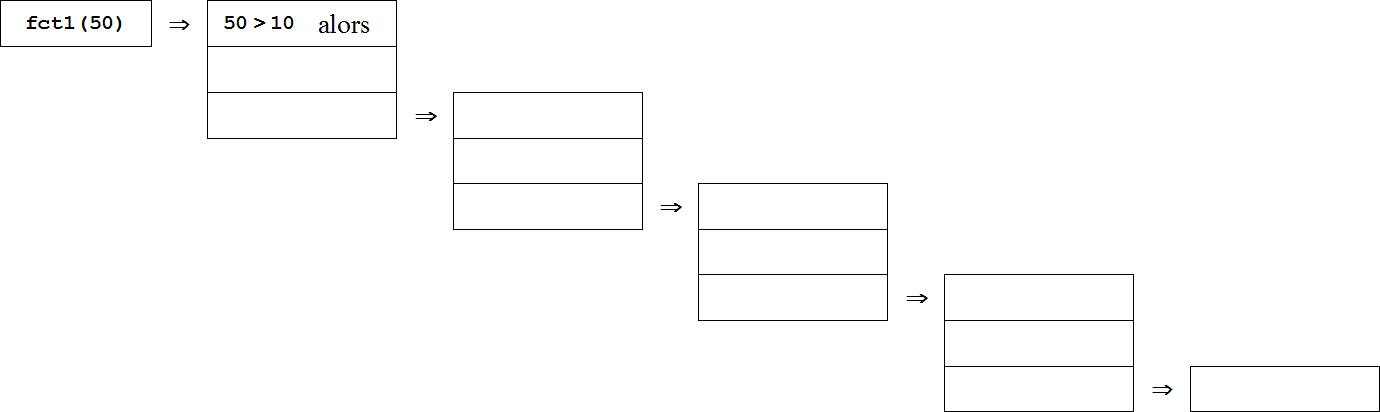
Pile d'appels 01

Le programme complet
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
from turtle import *

def rectangle(n):
    """
    n - int, entier strictement positif
    """
    color('white', 'blue')
    begin_fill()
    for _ in range(2):
        forward(10)
        left(90)
        forward(n)
        left(90)
    end_fill()
    forward(10)

def fct1(n):
    """
    n - int
    """
    if n > 10:
        rectangle(n)
        fct1(n-10)

if __name__ == "__main__":
    TurtleScreen._RUNNING = True
    hideturtle()
    speed(0)
    fct1(50)
    exitonclick()
Réponses

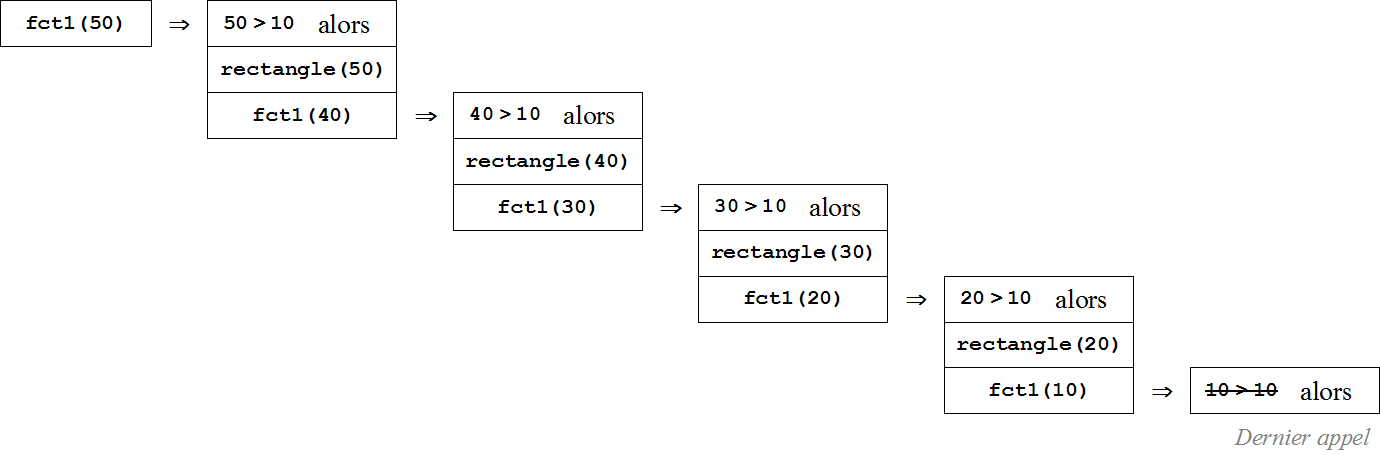
Le rectangle est tracé avant l'appel récursif suivant : Pile d'appels 01

On en déduit le dessin suivant pour l'appel fct1(50) L'escalier descend

Un second exemple☘

On échange les instructions des lignes 22 et 23 pour définir la fonction récursive suivante :

17
18
19
20
21
22
23
def fct2(n):
    """
    n - int
    """
    if n > 10:
        fct2(n-10)
        rectangle(n)

On effectue l'appel fct2(50). Complétez la pile d'appel puis tracez la figure correspondante.

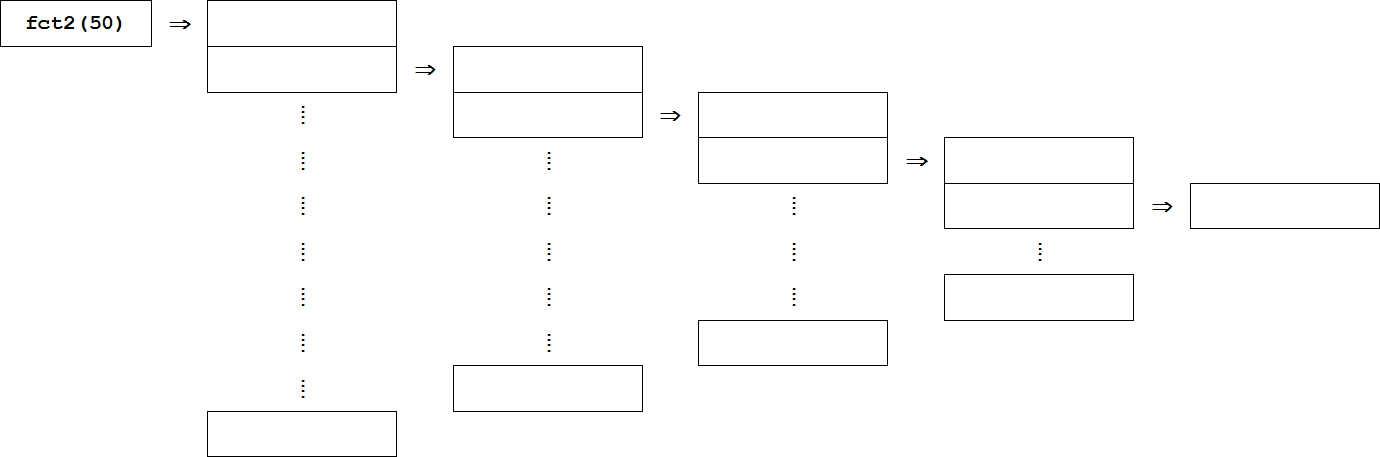
Pile d'appels 02

Le programme complet
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
from turtle import *

def rectangle(n):
    """
    n - int, entier strictement positif
    """
    color('white', 'blue')
    begin_fill()
    for _ in range(2):
        forward(10)
        left(90)
        forward(n)
        left(90)
    end_fill()
    forward(10)

def fct2(n):
    """
    n - int
    """
    if n > 10:
        fct2(n-10)
        rectangle(n)

if __name__ == "__main__":
    TurtleScreen._RUNNING = True
    hideturtle()
    speed(0)
    fct2(50)
    exitonclick()
Réponses

Lorsqu'on exécute fct2(50) :

  • On exécute fct2(40) donc on met en attente rectangle(50) ;
  • On exécute fct2(30) donc on met en attente rectangle(40) en priorité devant rectangle(50) car fct2(40) doit être exécuté avant rectangle(50) ;
  • On exécute fct2(20) donc on met en attente rectangle(30) en priorité devant rectangle(40) en priorité devant rectangle(50) ;
  • On exécute fct2(10) donc on met en attente rectangle(20) en priorité devant rectangle(30) en priorité devant rectangle(40) en priorité devant rectangle(50) ;
  • 10 n'est pas strictement supérieur à 10, les appels se terminent.
  • On dépile par ordre de priorité en traçant dans l'ordre rectangle(20), rectangle(30), rectangle(40) puis rectangle(50)

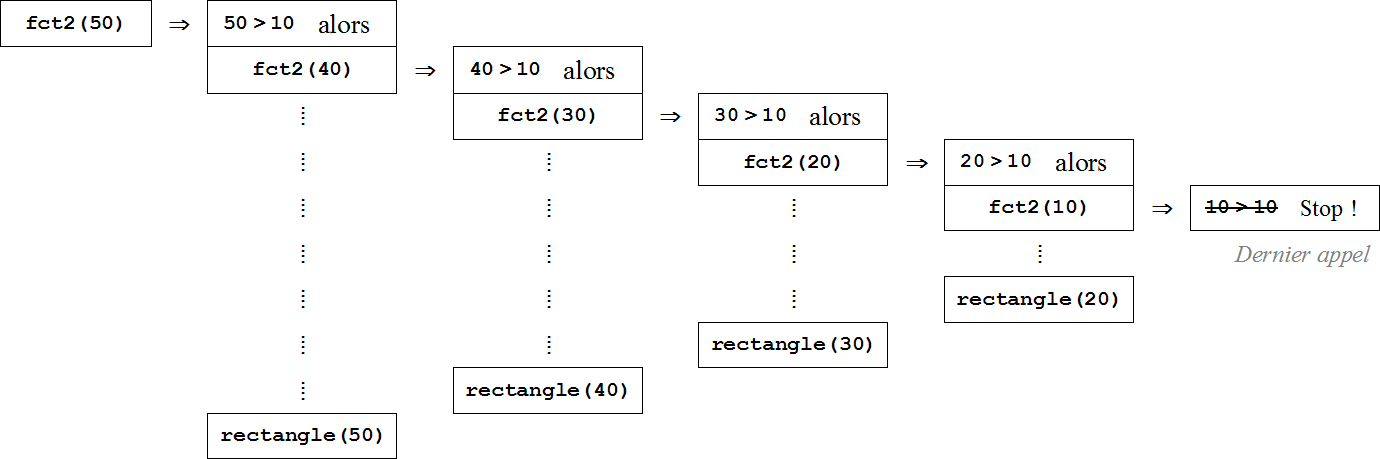
L'illustration ci-dessous permet de mieux visualiser l'empilement de ces appels : Pile d'appels 02

On en déduit le dessin suivant pour l'appel fct2(50) L'escalier descend

Complexité☘

Rappel

La complexité d'un algorithme se décompose généralement sous deux formes :

  • La complexité en temps : combien de temps prend un algorithme pour s'exécuter ?
    On ramène généralement cette question au décompte du nombre d'opérations élémentaires nécessaires pour le déroulement de l'algorithme.

  • La complexité en mémoire : quel espace en mémoire est nécessaire au déroulement de l'algorithme ?

On notera généralement n le nombre de données à traiter. La complexité est ensuite donnée comme un « ordre de grandeur » de n. Cet ordre de grandeur est souvent noté O (se lit « grand O ») :


Classe de complexité Type de complexité
O(1) constante
O(log(n)) logarithmique
O(n) linéaire
O(n × log(n)) quasi-linéaire
O(n²) quadratique
O(2n) exponentielle
O(n!) factorielle

Pour les fonctions récursives envisagées ci-dessous, on admet que la complexité en temps est proportionnelle au nombre d'appels récursifs.

Un premier exemple☘

On considère la fonction récursive suivante :

1
2
3
4
5
6
def descente(n):
    """
    n - int
    """
    if n > 0:
        descente(n-1)

  1. Combien d'appels à la fonction descente() sont réalisés lorsqu'on exécute l'instruction descente(5) ?
  2. Combien d'appels à la fonction descente() sont réalisés lorsqu'on exécute l'instruction descente(8) ?
  3. Donnez, en fonction de n, le nombre d'appels à la fonction descente() réalisés lorsqu'on exécute l'instruction descente(n).
  4. En déduire la complexité de cette fonction.
Éléments de réponse

La flèche « → » modélise l'appel suivant.

  1. descente(5) → descente(4) → descente(3) → descente(2) → descente(1) → descente(0) (0 n'est pas strictement supérieur à 0, c'est le dernier appel récursif).
    Lorsqu'on exécute l'instruction descente(5), on effectue 6 appels à la fonction descente().

  2. De la même manière, lorsqu'on exécute l'instruction descente(8), on effectue 9 appels à la fonction descente().

  3. Soit n est négatif ou nul, alors le test n > 0 n'est pas validé et il n'y a pas d'appel récursif à la fonction descente().
    Soit n est strictement positif. Les appels se déroulent alors ainsi :
    descente(n) → descente(n-1) → ... → descente(1) → descente(0).
    On effectue donc n+1 appels récursifs à la fonction descente().

  4. Ce nombre d'appels est un multiple de n : la complexité est linéaire.

Un deuxième exemple☘

On considère la fonction récursive suivante :

1
2
3
4
5
6
7
def piano(n):
    """
    n - int
    """
    if n > 0:
        piano(n-1)
        piano(n-1)

  1. Combien d'appels à la fonction piano() sont réalisés lorsqu'on exécute l'instruction piano(3) ?
  2. Combien d'appels à la fonction piano() sont réalisés lorsqu'on exécute l'instruction piano(5) ?
  3. Donnez, en fonction de n, le nombre d'appels à la fonction piano() réalisés lorsqu'on exécute l'instruction piano(n).
  4. En déduire la complexité de cette fonction.
Éléments de réponse

  1. piano(3) appelle deux fois piano(2).
    Chaque appel de piano(2) appelle deux fois piano(1).
    Chaque appel de piano(1) appelle deux fois piano(0).
    Chaque appel de piano(0) termine car 0 n'est pas strictement supérieur à 0.
    Le nombre total d'appels générés par piano(3) est donc 1+2+4+8 = 2^4 - 1.

  2. De la même manière, lorsqu'on exécute l'instruction piano(5), on effectue 2^6 - 1 appels à la fonction piano().

  3. Soit n est négatif ou nul, alors le test n > 0 n'est pas validé et il n'y a pas d'appel récursif à la fonction piano().
    Soit n est strictement positif. On note T(n) le nombre d'appels engendrés par l'exécution de piano(n). Dès lors, T(n) = 2 T(n-1) = 2 \times 2 T(n-2) = \cdots = 2^n \; T(0) appels.
    On effectue donc 2^n appels piano(0). Le nombre total d'appels engendrés par piano(n) est 1+2^1+2^2+...+2^n = 2^{n+1}-1.

  4. Ce nombre d'appels est, à une constante près, une puissance n-ième de 2 donc la complexité est exponentielle.