Aller au contenu

Exercices pour débuter☘

Les exercices ci-dessous ont pour but de vous familiariser avec la programmation de fonction récursive.
Prenez l'habitude de revenir vous entraîner régulièrement avec ces exercices tout au long de l'année. Ils sont généralement accompagnés de pistes et de leur solution pour vous permettre de progresser.

Rappels

  • Chaque programme Python doit être sauvegardé sous forme de fichier texte avec l'extension .py.
    Enregistrez ce fichier dans le dossier [D03-Récursivité] avec le nom donné à l'exercice : ProgD03.51.py, ProgD03.52.py, etc...
  • Pour exécuter ce programme, il suffit de le sauvegarder puis d'appuyer sur la touche [F5].

Prog D03.51☘

Écrire une fonction récursive Python spirale(cote, delta, angle, n) utilisant la tortue. Le paramètre cote est la longueur du premier segment tracé, delta est la quantité ajoutée à cette longueur de segment après chaque virage, le virage étant paramétré par angle. Enfin, n représente le nombre de segments tracés.

Par exemple :

  • l'appel spirale(10, 5, 90, 30) devrait donner une figure qui commence ainsi : Spirale01

  • l'appel spirale(2, 3, 120, 40) devrait donner :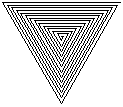 Spirale01

Ces fonctions sont appliquées à une tortue « anonyme », c'est-à-dire sans programmation orientée objet.

Une solution
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
from turtle import *

def spirale(cote, delta, angle, n = 20) :
    if n > 0 :
        forward(cote)
        right(angle)
        spirale(cote + delta, delta, angle, n-1)

if __name__ == "__main__":
    TurtleScreen._RUNNING = True
    hideturtle()
    speed(0)
    spirale(2, 3, 120, 40)
    exitonclick()

Prog D03.52☘

On veut calculer la somme S = 1+2+3+...+n où n est un entier naturel. Le but de cet exercice est de programmer une version récursive du calcul de cette somme.

  1. Déterminez le (ou les) cas de base.
  2. Exprimer somme(n) en fonction de somme(n-1).
  3. En déduire la définition récursive de la fonction somme() : 
    1
2
3
4
5
    def somme_rec(n):
    """
    n - entier positif ou nul
    Sortie: entier - la somme des entiers naturels de 1 à n
    """
Des réponses

  1. n est un entier naturel. Par conséquent, les cas de base sont somme(0) = 0 et somme(1) = 1.

  2. somme(n) = somme(n-1) + n.

  3. Version récursive de la fonction somme() : 

    1
2
3
4
5
6
7
8
9
    def somme_rec(n):
    """
    n - entier positif ou nul
    Sortie: entier - la somme des entiers naturels de 1 à n
    """
    if n <= 1 :
        return n
    else:
        return somme_rec(n-1) + n

Prog D03.53☘

La récursivité trouve une application immédiate avec les suites définies par récurrence en mathématiques.

Compléter la définition récursive de la fonction u() qui permet de calculer la valeur du terme d'indice n de la suite définie par u_0 = 2 et la formule u_{n+1} = 3 u_n.

1
2
3
4
5
def u(n):
    """
    n - entier positif ou nul
    Sortie: entier - le terme d'indice n de la suite
    """
Une solution
1
2
3
4
5
6
7
8
9
def u(n):
    """
    n - entier positif ou nul
    Sortie: entier - le terme d'indice n de la suite
    """
    if n == 0 :
        return 2
    else:
        return 3*u(n-1)

Prog D03.54☘

On appelle SECRET de protection n, une chaîne de caractères composée de n parenthèses ouvrantes, puis du mot SECRET suivi de n parenthèses fermantes. Par exemple :

  • un SECRET de protection 4 est la chaîne de caractères : 

    "((((SECRET))))"

  • un SECRET de protection 0 est la chaîne de caractères : 

    "SECRET"

Le but de cet exercice est de programmer une version récursive de la fabrication d'un SECRET de protection n.

  1. Déterminez le (ou les) cas de base.
  2. Exprimer protection(n) en fonction de protection(n-1).
  3. En déduire la définition récursive de la fonction protection() : 
    1
2
3
4
5
    def protection(n):
    """
    n - entier positif ou nul
    Sortie: str - Le mot "SECRET" encadré de n parenthèses
    """
Des réponses

  1. n est un entier naturel. Par conséquent, le cas de base est protection(0) = "SECRET".

  2. protection(n) = "(" + protection(n-1) + ")".

  3. Version récursive de la fonction protection() : 

    1
2
3
4
5
6
7
8
9
    def protection(n):
    """
    n - entier positif ou nul
    Sortie: str - Le mot "SECRET" encadré de n parenthèses
    """
    if n == 0:
        return "SECRET"
    else:
        return "(" + protection(n-1) + ")"

Prog D03.55☘

Programmer une fonction qui permet de calculer x^n, où n est un entier positif.

Une piste

Prenez le temps de réfléchir au cas de base.

Une solution
1
2
3
4
5
6
7
8
9
def puissance(x, n):
    """
    n - entier positif ou nul
    Sortie: int - x puissance n
    """
    if n == 0:
        return 1
    else:
        return x * puissance(x, n-1)

Prog D03.56☘

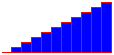escaliers Le but de cet exercice est de faire tracer un escalier par la tortue (anonyme, c'est-à-dire sans POO). Toutes les marches ont la même largeur. L'image ci-contre présente un exemple possible.

  1. Complétez la définition suivante permettant à la tortue de dessiner une marche d'escalier. 

    1
2
3
4
5
    def marche(largeur, hauteur):
    """
    largeur, hauteur - entiers strictement positifs
    Sortie: None - La tortue trace un rectangle de dimensions largeur et hauteur
    """

    Une réponse pour le 1.
     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
    from turtle import *

def marche(largeur, hauteur):
    """
    largeur, hauteur - entiers strictement positifs
    Sortie: None - La tortue trace un rectangle de dimensions largeur et hauteur
    """
    color('red', 'blue')    # contour en rouge, intérieur en bleu
    begin_fill()
    forward(largeur)
    left(90)
    forward(hauteur)
    left(90)
    forward(largeur)
    left(90)
    forward(hauteur)
    left(90)
    end_fill()

  2. Pour construire un escalier de n marches, il suffit de savoir construire une marche et un escalier de n-1 marches 😈.
    En déduire une fonction Python récursive dessinant un escalier de n marches. 

    1
2
3
4
5
6
    def escalier(largeur, n) :
    """
    largeur - int, largeur d'une marche
    n - int, nombre de marches de l'escalier
    Sortie: None - La tortue trace l'escalier de n marches
    """

    Une réponse pour le 2.
     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
    from turtle import *

def escalier(largeur, n) :
"""
largeur - int, largeur d'une marche
n - int, nombre de marches de l'escalier
Sortie: None - La tortue trace l'escalier de n marches
"""
if n > 0 :
    marche(largeur, 5*n)
    backward(largeur)
    escalier(largeur, n-1)
    Une autre réponse pour le 2.
     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
    from turtle import *

def escalier(largeur, n) :
"""
largeur - int, largeur d'une marche
n - int, nombre de marches de l'escalier
Sortie: None - La tortue trace l'escalier de n marches
"""
if n > 0 :
    escalier(largeur, n-1)
    forward(largeur)
    marche(largeur, 5*n)

  3. Vous pouvez tester vos fontions à l'aide des instructions ci-dessous : 

    14
15
16
17
18
19
    if __name__ == "__main__":
    TurtleScreen._RUNNING = True
    hideturtle()
    speed(0)
    escalier(10, 10)
    exitonclick()

    Le programme complet
     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
    from turtle import *

def marche(largeur, hauteur):
    """
    largeur, hauteur - entiers strictement positifs
    Sortie: None - La tortue trace un rectangle de dimensions largeur et hauteur
    """
    color('red', 'blue')    # contour en rouge, intérieur en bleu
    begin_fill()
    forward(largeur)
    left(90)
    forward(hauteur)
    left(90)
    forward(largeur)
    left(90)
    forward(hauteur)
    left(90)
    end_fill()

def escalier(largeur, n) :
    """
    largeur - int, largeur d'une marche
    n - int, nombre de marches de l'escalier
    Sortie: None - La tortue trace l'escalier de n marches
    """
    if n > 0 :
        marche(largeur, 5*n)
        backward(largeur)
        escalier(largeur, n-1)

def escalier2(largeur, n) :
    """
    largeur - int, largeur d'une marche
    n - int, nombre de marches de l'escalier
    Sortie: None - La tortue trace l'escalier de n marches
    """
    if n > 0 :
        escalier2(largeur, n-1)
        forward(largeur)
        marche(largeur, 5*n)


if __name__ == "__main__":
TurtleScreen._RUNNING = True
hideturtle()
speed(0)
escalier(10, 10)
exitonclick()