Exercices pour s'entraîner☘

Les exercices ci-dessous ont pour but de vous familiariser avec la programmation de fonction récursive.
Prenez l'habitude de revenir vous entraîner régulièrement avec ces exercices tout au long de l'année. Ils sont généralement accompagnés de pistes et de leur solution pour vous permettre de progresser.

Rappels

Chaque programme Python doit être sauvegardé sous forme de fichier texte avec l'extension .py.
Enregistrez ce fichier dans le dossier [D03-Récursivité] avec le nom donné à l'exercice : ProgD03.61.py, ProgD03.62.py, etc...
Pour exécuter ce programme, il suffit de le sauvegarder puis d'appuyer sur la touche [F5].

Prog D03.61☘

On rappelle la définition de la fonction rectangle() utilisée dans le cours :

from turtle import *

def rectangle(n):
    """
    n - int, entier strictement positif
    """
    color('white', 'blue')
    begin_fill()
    for _ in range(2):
        forward(10)
        left(90)
        forward(n)
        left(90)
    end_fill()
    forward(10)


if __name__ == "__main__":
    TurtleScreen._RUNNING = True
    hideturtle()
    speed(0)
    rectangle(50)
    exitonclick()

En utilisant cette fonction, complétez le code récursif de la fonction fct3() telle que l'appel fct3(100) permet de tracer la figure ci-dessous :
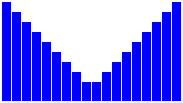
L'escalier part dans tous les sens

def fct3(n):
    """
    n - int
    """

Une illustration par vidéo

Voici une petite vidéo du tracé pour visualiser l'empilement des instructions lors de l'appel fct3(100) :

Une piste

Ne pas oublier le travail réalisé dans le cours sur les piles d'appels...

Une solution

def fct3(n):
    """
    n - int
    """
    if n > 10:
        rectangle(n)
        fct3(n-10)
        rectangle(n)

Exercice D03.62☘

On considère la fonction suivante :

def fct4(n):
    """
    n - entier
    """
    if n > 10:
        fct4(n-10)
        rectangle(n)
        fct4(n-10)

Réalisez à la main le dessin obtenu avec l'appel fct4(50). Sur votre cahier, un carreau représente 10 pixels.
Vérifiez ensuite en effectuant cet appel dans la console Python.

Réponse et explications

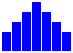
On pourrait croire que la figure obtenue est : On monte, on descend

Mais l'exécution de fct4(50) dans la console donne cette animation :

En effet :

fct4(50) exécute fct4(40) puis, une fois cette exécution terminée trace rectangle(50) et enfin exécute à nouveau fct4(40) :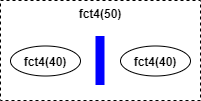
fct4(40) exécute fct4(30) puis, une fois cette exécution terminée, trace rectangle(40) et enfin exécute à nouveau fct4(30) :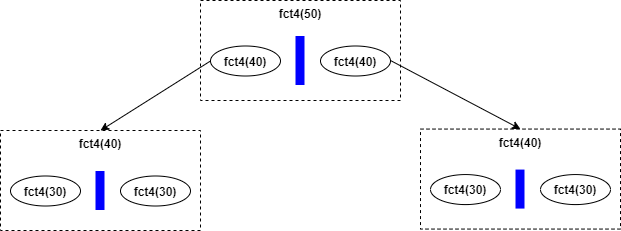
fct4(30) exécute fct4(20) puis, une fois cette exécution terminée, trace rectangle(30) et enfin exécute à nouveau fct4(20) :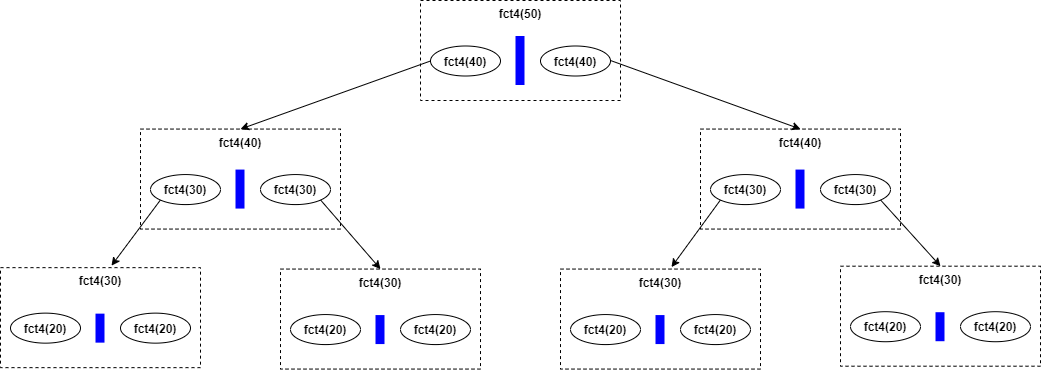
et ainsi de suite... jusqu'à l'appel fct4(10) qui n'exécute rien puisque l'argument n'est pas strictement supérieur à 10 :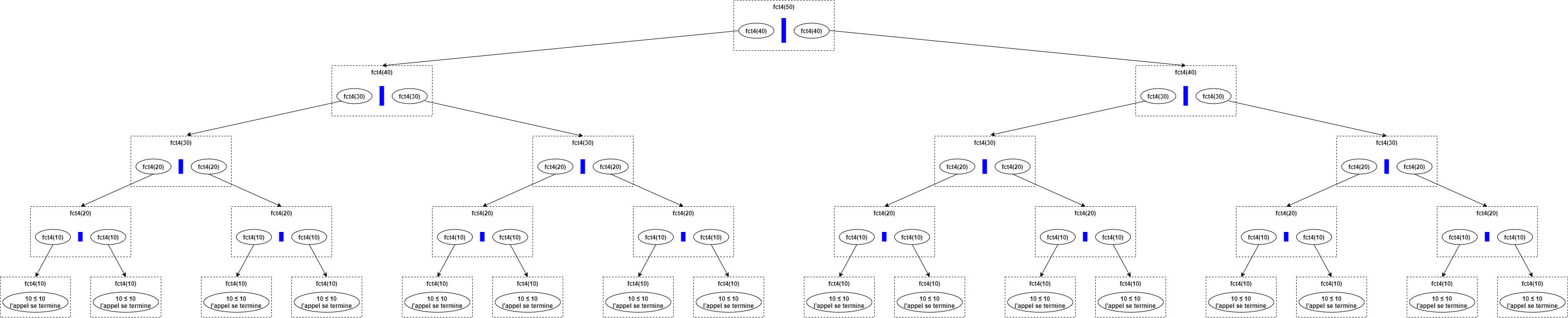

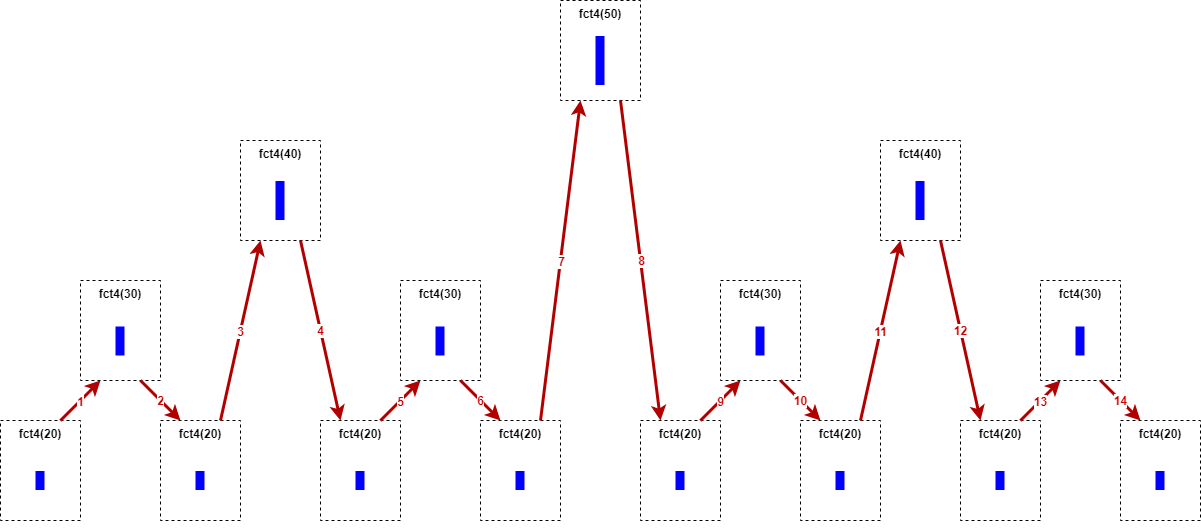
En remontant la pile d'appels de gauche à droite, on obtient ainsi la figure dessinée par la tortue : Pile d'appel et dessin

Prog D03.63☘

On rappelle ci-dessous l'algorithme d'Euclide, qui permet de calculer le pgcd de deux entiers positifs :

On calcule le reste r de la division de a par b
Tant que le reste n'est pas nul, a prend la valeur de b et b, celle de r
Le PGCD est le dernier reste non nul.

Complétez une version récursive de ce calcul :

def pgcd(a, b):
    """
    a, b – entiers positifs
    Sortie : entier – le PGCD de a et b
    """

Exemple de test

>>> pgcd(91, 143)
13

Des pistes

Pensez au cas de base ;
Pensez à l'expression d'un appel en fonction du suivant.

Définition récursive explicite

Pour tout entier a (non nul), pgcd(a, 0) = a.
Pour tous les entiers a et b non nuls, pgcd(a, b) = pgcd(b, r), où r est le reste dans la division euclidienne de a par b.

Une solution

def pgcd(a, b):
    """
    a, b – entiers positifs
    Sortie : entier – le PGCD de a et b
    """
    if b == 0 :
        return a
    else :
        return pgcd(b, a%b)

Prog D03.65*☘

On définit la suite de Fibonacci par $F_0 = F_1 = 1$ et, pour tout entier naturel $n$ : $F_{n+2} = F_{n+1} + F_n$ .

Complétez une version récursive du calcul d'un terme de cette suite :

def fibonacci(n):
    """
    n – entier positif ou nul
    Sortie: entier – le nombre F_n
    """

Un test

>>> fibonacci(13)
377

Une solution

def fibonacci(n):
    """
    n – entier positif ou nul
    Sortie: entier – le nombre F_n
    """
    if n <= 1 :
        return 1
    else :
        return fibonacci(n-1) + fibonacci(n-2)

On effectue l'appel fibonacci(7). Représentez sur un cahier l'arbre d'appels correspondant.

Une solution

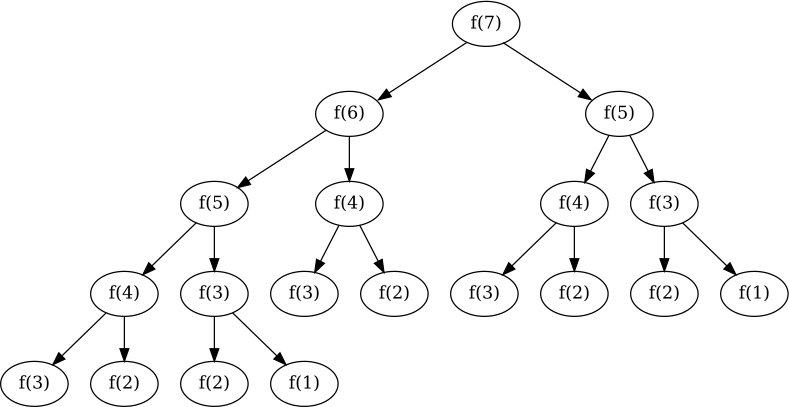
Arbre d'appels

Visualisation de l'arbre dans la console

Une fonction peut permet de créer ci-dessous permet d'une fonction récursive :

&qu decalage def return return

Les instructions

< >>>

renvoient :

< | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | 

prendre pour paramètre une autre fonction, cela des décorateurs. Ainsi, la fonction tracer() de visualiser dans la console l'arbre des appels class="linenos">

 1 class="code">def tracer(f): ot;"" f - une fonction récursive Sortie: None - Affiche l'arbre des appels de la fonction f """ = 0 g(x): nonlocal decalage                         # decalage est une variable de tracer(), pas de g() >print('|        ' * decalage, end='') >print(f'|Appel {f.__name__}({x})')        # f.__name__ sera remplacé par le nom de la fonction "tracée" decalage +=1 imagefx = f(x) >print('|        ' * decalage, end='') >print('|-> renvoie {}'.format(imagefx) ) decalage -= 1 imagefx g pre>>>> fibonacci = tracer(fibonacci) fibonacci(7) pre>|Appel fibonacci(7) |Appel fibonacci(6) |        |Appel fibonacci(5) |        |        |Appel fibonacci(4) |        |        |        |Appel fibonacci(3) |        |        |        |        |Appel fibonacci(2) |        |        |        |        |        |Appel fibonacci(1) |        |        |        |        |        |        |-> renvoie 1 |        |        |        |        |        |Appel fibonacci(0) |        |        |        |        |        |        |-> renvoie 1 |        |        |        |        |        |-> renvoie 2 |        |        |        |        |Appel fibonacci(1) |        |        |        |        |        |-> renvoie 1 |        |        |        |        |-> renvoie 3 |        |        |        |Appel fibonacci(2) |        |        |        |        |Appel fibonacci(1) |        |        |        |        |        |-> renvoie 1 |        |        |        |        |Appel fibonacci(0) |        |        |        |        |        |-> renvoie 1 |        |        |        |        |-> renvoie 2 |        |        |        |-> renvoie 5 |        |        |Appel fibonacci(3) |        |        |        |Appel fibonacci(2) |        |        |        |        |Appel fibonacci(1) |        |        |        |        |        |-> renvoie 1 |        |        |        |        |Appel fibonacci(0) |        |        |        |        |        |-> renvoie 1 |        |        |        |        |-> renvoie 2 |        |        |        |Appel fibonacci(1) |        |        |        |        |-> renvoie 1 |        |        |        |-> renvoie 3 |        |        |-> renvoie 8 |        |Appel fibonacci(4) |        |        |Appel fibonacci(3) |        |        |        |Appel fibonacci(2) |        |        |        |        |Appel fibonacci(1) |        |        |        |        |        |-> renvoie 1 |        |        |        |        |Appel fibonacci(0) |        |        |        |        |        |-> renvoie 1 |        |        |        |        |-> renvoie 2 |        |        |        |Appel fibonacci(1) |        |        |        |        |-> renvoie 1 |        |        |        |-> renvoie 3 |        |        |Appel fibonacci(2) |        |        |        |Appel fibonacci(1) |        |        |        |        |-> renvoie 1 |        |        |        |Appel fibonacci(0) |        |        |        |        |-> renvoie 1 |        |        |        |-> renvoie 2 |        |        |-> renvoie 5 |        |-> renvoie 13 |Appel fibonacci(5) |        |Appel fibonacci(4) |        |        |Appel fibonacci(3) |        |        |        |Appel fibonacci(2) |        |        |        |        |Appel fibonacci(1) |        |        |        |        |        |-> renvoie 1 |        |        |        |        |Appel fibonacci(0) |        |        |        |        |        |-> renvoie 1 |        |        |        |        |-> renvoie 2 |        |        |        |Appel fibonacci(1) |        |        |        |        |-> renvoie 1 |        |        |        |-> renvoie 3 |        |        |Appel fibonacci(2) |        |        |        |Appel fibonacci(1) |        |        |        |        |-> renvoie 1 |        |        |        |Appel fibonacci(0) |        |        |        |        |-> renvoie 1 |        |        |        |-> renvoie 2 |        |        |-> renvoie 5 |        |Appel fibonacci(3) |        |        |Appel fibonacci(2) |        |        |        |Appel fibonacci(1) |        |        |        |        |-> renvoie 1 |        |        |        |Appel fibonacci(0) |        |        |        |        |-> renvoie 1 |        |        |        |-> renvoie 2 |        |        |Appel fibonacci(1) |        |        |        |-> renvoie 1 |        |        |-> renvoie 3 |        |-> renvoie 8 |-> renvoie 21



Expliquez en quoi ce script est inefficace et proposer une version non
récursive plus efficace, en complexité linéaire.
Une solution
L'arbre d'appel permet de voir que certains calculs sont lancés à
plusieurs reprises, d'où l'inefficacité de ce script. Les temps de
calcul deviennent rapidement excessifs : essayez par exemple de
calculer fibonacci(50) avec ce script...
Une version itérative plus efficace est, par exemple :
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12 def fibonacci(n):
    """
    n – entier positif ou nul
    Sortie: entier – le nombre F_n
    """
    f0 = 1
    f1 = 1
    for i in range(1, n):
        f2 = f0 + f1
        f0 = f1
        f1 = f2
    return f1


Prog D03.66*☘
On dispose d'un tableau contenant des entiers ou des tableaux d'entiers, ou
des tableaux de tableaux d'entiers ou des tableaux de tableaux de tableaux
d'entiers ou ...
Par exemple :
tab = [3, [2,3,[4,5,6], [2,[3,5]] ] , 8, [[[[ 4, [1] ]]]], 15 ]

Complétez la définition récursive de la fonction somme_tab_imbriques,
qui prend pour paramètre un tableau imbriqué et qui renvoie la somme de
l'ensemble des entiers contenus dans ce tableau.
1
2
3
4
5 def somme_tab_imbriques(tab):
    """
    tab - list ou int, tableau imbriqué d'entiers ou bien entier tout seul
    Sortie: int - somme de tous les éléments entiers de ce tableau
    """



Un test
>>> tab = [2, 3, 4, [2, 5, [4, 7], 8], [2, [[[7]]]], [] ]
>>> somme_tab_imbriques(tab)
44


Une piste
On pourra utiliser la fonction isinstance() :
>>> isinstance(8, int)    # 8 est-il de type int ?
True

>>> isinstance(8, list)   # 8 est-il de type list ?
False

>>> isinstance([8], list)
True


Une autre piste
Le cas de base intervient quand le paramètre est un entier. Il suffit
alors de renvoyer cette valeur.
Pour comprendre les appels récursifs à réaliser, il suffit de se rappeler
que la somme des éléments d'un tableau imbriqué est la somme totale des
tableaux imbriqués contenus dans ce tableau.

En d'autres termes, si tab est de la forme tab = [A, B, C] où
A, B et C sont des tableaux imbriqués alors
somme_tab_imbriques(tab) est égale à somme_tab_imbriques(A) +
somme_tab_imbriques(B) + somme_tab_imbriques(C).

Une solution
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14 def somme_tab_imbriques(tab):
    """
    tab - list ou int, tableau imbriqué d'entiers ou bien entier tout seul
    Sortie: int - somme de tous les éléments entiers de ce tableau
    """
    if tab == [] :
        return 0
    elif isinstance(tab, int):
        return tab
    else :
        somme = 0
        for elt in tab :
            somme = somme + somme_tab_imbriques(tab)
        return somme