Ecriture d'un entier en base 2☘

C'est le système de base 2 qu'utilisent les ordinateurs.

Définition

Ecrire un entier $n$ en base deux, c'est écrire cet entier $n$ sous la forme : $$ n = c_0 + c_1 \times 2 + c_2 \times 2^2 + c_3 \times 2^3 + \dots $$ où chaque coefficient $c_i$ est un chiffre de cette base : $0$ ou $1$ .

L'écriture d'un entier en base 2 sera appelée écriture binaire de l'entier. Un chiffre en binaire est donc parfois appelé bit, mot qui est un raccourci de binary digit (chiffre binaire).
Ainsi, en base 2 :

le coefficient $c_0$ (coefficient de $2^0$ ) est appelé bit de poids 0 ;
le coefficient $c_1$ (coefficient de $2^1$ ) est appelé bit de poids 1 ;
le coefficient $c_2$ (coefficient de $2^2$ ) est appelé bit de poids 2 ;
etc...

Vocabulaire

Un nombre binaire de huit bits (huit chiffres) est aussi appelé un octet.

Exemple☘

L'entier binaire $n = (1101)_{2}$ désigne l'entier de base 10 $n = 1\times 2^3 + 1\times 2^2 + 0 \times 2^1 + 1\times 2^0$ , c'est à dire $n = 8 + 4 + 0 + 1$ soit l'entier $n = 13$ .

Remarque

Comme le suggèrent les écritures ci-dessus, nous noterons en indice la base utilisée afin de distinguer, par exemple, les deux nombres : $(1101)_{2} = 1\times 2^3 + 1\times 2^2 + 0 \times 2^1 + 1\times 2^0$ et $(1101)_{10} = 1\times 10^3 + 1\times 10^2 + 0 \times 10^1 + 1\times 10^0$ .

Par convention, lorsque la base n'est pas indiquée en indice, cela sous-entend que le nombre est écrit en base 10.

Attention

Un abus de langage et d’utilisation a longtemps fait la correspondance 1 ko = 1000 octets. Or, ces valeurs ne sont pas égales car $10^3 \ne 2^{10}$ .
Toutefois, savoir que $2^{10} \approx 10^3$ peut simplifier le calcul mental et la recherche d'ordre de grandeur...

Conversion de binaire en décimal☘

L'écriture binaire d'un entier $n$ est une liste finie de $0$ et de $1$ . Il suffit d'associer à chaque chiffre $1$ son poids et d'additionner les puissances de $2$ ainsi obtenues pour obtenir l'écriture décimale de l'entier $n$ .

Une méthode rapide de conversion peut être effectuée en utilisant un tableau (attention à l'ordre : bit de poids 0 à droite !) :

Puissances de 2	...	2⁵	2⁴	2³	2²	2¹	2⁰
Valeur décimale	...	32	16	8	4	2	1
Nombre binaire	...

Exemple☘

Convertir le nombre $(1001 \, 0101)_2$ en base 10.

Une solution

On liste dans un tableau les puissances de 2 permettant de couvrir tous les chiffres de ce nombre. On remplit la dernière ligne avec l'écriture binaire du nombre donné :

Puissances de 2	2⁷	2⁶	2⁵	2⁴	2³	2²	2¹	2⁰
Valeur décimale	128	64	32	16	8	4	2	1
Nombre binaire	1	0	0	1	0	1	0	1

On ajoute toutes les valeurs décimales qui correspondent au bit $1$ : $128 + 16 + 4 + 1 = 149$ .
On en déduit l'écriture décimale de ce nombre binaire : $(1001 \, 0101)_{2} = (149)_{10}$ .

Conversion de décimal en binaire☘

Rappel - chiffres d'une écriture décimale

Pour obtenir, un à un, les chiffres d'une écriture décimale, on peut utiliser les Les divisions en cascade.
Raisonnons sur l'exemple de l'entier $n = 8643$ :

Le chiffre des unités de $n$ est le reste de la division euclidienne de $n$ par $10$ :
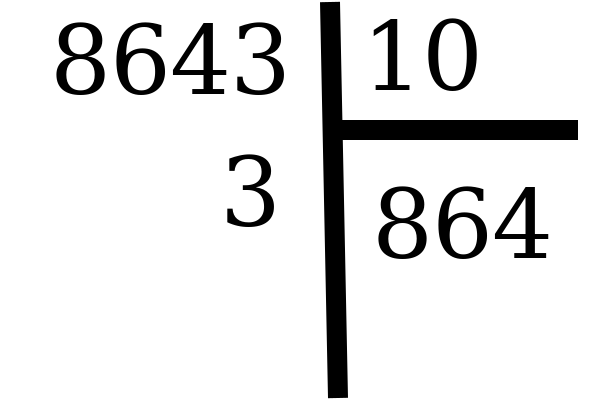Le chiffre des unités est donc 3.
Le chiffre des dizaines est le chiffre des unités du quotient précédent:
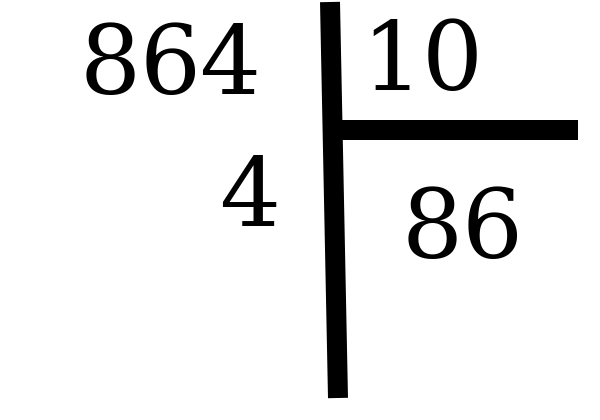Le chiffre des dizaines est donc 4.
Et on continue ainsi jusqu'à obtenir un quotient nul...

On peut résumer ce raisonnement par une "division en cascade":
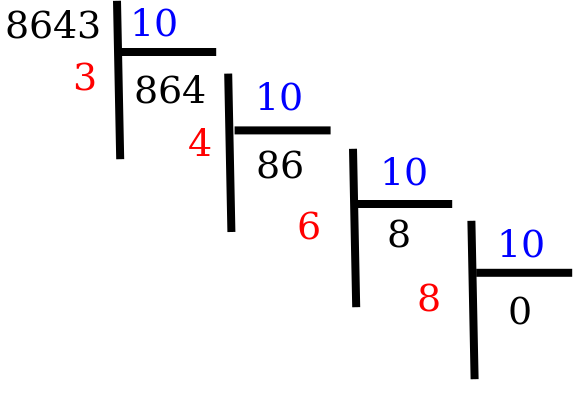Dans cette division en cascade, on voit que les restes successifs (chiffres rouges) sont les chiffres de l'entier (obtenu à contre-sens de l'écriture usuelle puisqu'on obtient en premier le chiffre des unités).

Lorsqu'on obtient un quotient (nombre noir) nul, on arrête la cascade.

Pour déterminer l'écriture binaire d'un nombre entier (décimal), deux méthodes sont possibles :

Les divisions en cascade en remplaçant le diviseur $10$ par le diviseur $2$ (cf. le rappel ci-dessus) ;
Les soustractions successives en utilisant un tableau de conversion (attention à l'ordre : bit de poids 0 à droite !) :

Puissances de 2	...	2⁵	2⁴	2³	2²	2¹	2⁰
Valeur décimale	...	32	16	8	4	2	1
Nombre binaire	...

Il faudra commencer par soustraire à l'entier la plus grande puissance de $2$ possible.

Exemple☘

Convertir le nombre $(91)_{10}$ en base 2.

Une solution par soustractions successives

On liste dans un tableau les puissances de 2 jusqu'à dépasser la valeur de l'entier (on s'arrète à $2^7$ car $128 \geqslant 91$ ) :

Puissances de 2	2⁷	2⁶	2⁵	2⁴	2³	2²	2¹	2⁰
Valeur décimale	128	64	32	16	8	4	2	1
Nombre binaire	0

Dans $91$ , la plus grande valeur possible est $64$ . On place le bit $1$ dans la case correspondante et on soustrait $64$ à $91$ : il reste $27$ .

Puissances de 2	2⁷	2⁶	2⁵	2⁴	2³	2²	2¹	2⁰
Valeur décimale	128	64	32	16	8	4	2	1
Nombre binaire	0	1

Dans $27$ , la plus grande valeur possible est $16$ . On place le bit $0$ dans les cases qui précèdent et le bit $1$ dans la case correspondante. On soustrait $16$ à $27$ : il reste $11$ .

Puissances de 2	2⁷	2⁶	2⁵	2⁴	2³	2²	2¹	2⁰
Valeur décimale	128	64	32	16	8	4	2	1
Nombre binaire	0	1	0	1

Dans $11$ , la plus grande valeur possible est $8$ . On place le bit $1$ dans la case correspondante et on soustrait $8$ à $11$ : il reste $3$ .

Puissances de 2	2⁷	2⁶	2⁵	2⁴	2³	2²	2¹	2⁰
Valeur décimale	128	64	32	16	8	4	2	1
Nombre binaire	0	1	0	1	1

Dans $3$ , la plus grande valeur possible est $2$ . On place le bit $0$ dans les cases qui précèdent et le bit $1$ dans la case correspondante. on soustrait $2$ à $3$ : il reste $1$ .

Puissances de 2	2⁷	2⁶	2⁵	2⁴	2³	2²	2¹	2⁰
Valeur décimale	128	64	32	16	8	4	2	1
Nombre binaire	0	1	0	1	1	0	1

Enfin, on place le bit $1$ dans le case de valeur $1$ :

Puissances de 2	2⁷	2⁶	2⁵	2⁴	2³	2²	2¹	2⁰
Valeur décimale	128	64	32	16	8	4	2	1
Nombre binaire	0	1	0	1	1	0	1	1

On conclut $(91)_{10} = (101 \, 1011)_2$ .

Une solution par divisions successives

On effectue des divisions par 2 « en cascade » à partir de 91 jusqu'à obtenir un quotient nul :
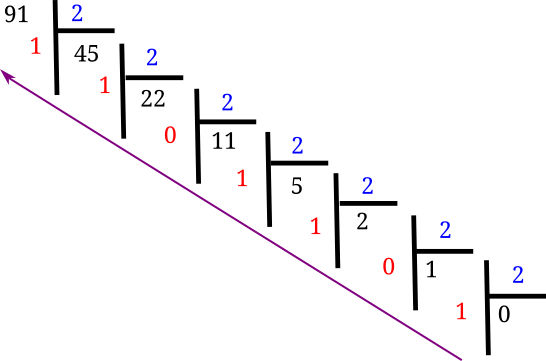
On lit à l'envers les restes obtenus pour en déduire l'écriture en base 2 de 91 : $(91)_{10} = (101 \, 1011)_2$ .