Ecriture d'un entier en base 16

Les circuits mémoires d'un ordinateurs sont groupés par octets (8 bits). Une architecture 32 bits est constituée de quatre octets pouvant représenter jusqu'à 4 294 967 295 valeurs distinctes. A vous de faire le calcul pour 64 bits...

Utiliser la base 2 devient vite très fastidieux en raison du nombre de positions nécessaires pour l'écriture d'un (grand) entier dans cette base. Il nous faut donc une autre base qui permette de simplifier cette écriture tout en ayant une correspondance rapide avec la base 2 : ce sera le système hexadécimal, de base 16.

Ce système nécessite d'utiliser 16 chiffres. En plus des dix chiffres de la base 10, on utilisera les lettres A, B, C, D, E et F avec la correspondance suivante :

Base 10	10	11	12	13	14	15
Base 16	A	B	C	D	E	F

Définition

Ecrire un entier $n$ en base seize, c'est écrire cet entier $n$ sous la forme : $$ n = c_0 + c_1 \times 16 + c_2 \times 16^2 + c_3 \times 16^3 + \dots $$ où chaque coefficient $c_i$ est un chiffre de cette base : $0$, $1$, $2$, $3$, $4$, $5$, $6$, $7$, $8$, $9$, $A$, $B$, $C$, $D$, $E$ ou $F$.

Conversion de binaire à hexadécimal

Comme $16 = 2^4$, il est possible de passer d'une écriture binaire à une écriture hexadécimale de la façon suivante :

1. On regroupe les bits de l'écriture binaire par paquets de quatre, en ajoutant au besoin à gauche des $0$ pour que le nombre de bits soit un multiple de 4.

2. On traduit ensuite chaque paquet de 4 bits par un chiffre en base 16 en suivant le tableau de conversion (à savoir refaire) :

   Base 10	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
   Base 2	0000	0001	0010	0011	0100	0101	0110	0111	1000	1001	1010	1011	1100	1101	1110	1111
   Base 16	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F

3. On « concatène » ces écritures en base $16$ : cela donne l'écriture complète de l'entier en base $16$.

Exemple

Appliquer la méthode précédente pour donner l'écriture en base $16$ de l'entier binaire $n = (101 \, 1101)_{2}$.

Une solution

1. On regroupe les bits par paquets de 4 depuis la droite, en ajoutant des $0$ « inutiles » si besoin : $n = (101 \, 1101)_{2}$ est réécrit $n = (0101 \, 1101)_{2}$.

2. On traduit chaque paquet de 4 bits avec le chiffre hexadécimal correspondant : le paquet $(0101)_{2}$ se traduit par $(5)_{16}$ et le paquet $(1101)_{2}$ se traduit par $(D)_{16}$.

3. L'écriture hexadécimale de $n = (101 \, 1101)_{2}$ est alors : $n = (5D)_{16}$.

Explication succincte

Sans rentrer dans des écritures trop formelles, on peut expliquer « pourquoi ça marche » avec l'exemple précédent.

On remarque déjà que sur 4 bits, on peut écrire en binaire les entiers de $(0000)_{2} = 0$ à $(1111)_{2} = 15$, ce qui correspond aux chiffres de la base $16$ (cf. le tableau de conversion).

De plus, $n = (101 \, 1101)_{2}$ se réécrit en base $10$ : $$ n = \left( 0\times 2^7 + 1 \times 2^6 + 0\times 2^5 + 1\times 2^4 \right) + \left( 1\times 2^3 + 1 \times 2^2 + 0\times 2^1 + 1\times 2^0 \right) $$ ou encore, après avoir factorisé par $2^4$ : $$ n = \left( 0\times 2^3 + 1 \times 2^2 + 0\times 2^1 + 1\times 2^0 \right) \times 2^4 + \left( 1\times 2^3 + 1 \times 2^2 + 0\times 2^1 + 1\times 2^0 \right) $$ c'est-à-dire : $$ n = \left( 0\times 2^3 + 1 \times 2^2 + 0\times 2^1 + 1\times 2^0 \right) \times 16^1 + \left( 1\times 2^3 + 1 \times 2^2 + 0\times 2^1 + 1\times 2^0 \right) \times 16^0 $$

On se convaincra facilement que la démarche est générique.
On aboutit ainsi bien à une écriture de la forme $n = c_0 + c_1 \times 16 + c_2 \times 16^2 + c_3 \times 16^3 + \dots$ où chaque coefficient $c_i$ est compris entre $0$ et $15$, c'est-à-dire représente un chiffre en base $16$.

Conversion de hexadécimal à binaire

On utilise le processus « inverse » de celui qui nous a permis de passer du binaire à l'hexadécimal : chacun des chiffres hexadécimaux est remplacé par sa traduction en binaire sur 4 bits (toujours en utilisant le tableau de conversion) :

Base 10	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Base 2	0000	0001	0010	0011	0100	0101	0110	0111	1000	1001	1010	1011	1100	1101	1110	1111
Base 16	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F

Exemple

Appliquer ce procédé pour donner l'écriture binaire de l'entier hexadécimal $n = (C8)_{16}$.

Une solution

1. On traduit chaque chiffre hexadécimal par le paquet de 4 bits correspondant : le chiffre $(C)_{16}$ se traduit par le paquet $(1100)_{2}$ et le chiffre $(8)_{16}$ se traduit par le paquet $(1000)_{2}$.

2. L'écriture binaire de $n = (A2)_{16}$ est alors $n = (1100 \, 1000)_{2}$.

Conversion de hexadécimal à décimal

L'écriture hexadécimale d'un entier $n$ est une liste finie de chiffres compris entre $0$ et $F$. Pour obtenir l'écriture décimale de l'entier $n$, il suffit :

1. d'associer à chaque chiffre son poids ;

2. de multiplier ce chiffre par la puissance de $16$ correspondante ;

3. d'additionner les valeurs ainsi obtenues.

Exemple

Convertir le nombre $(5B2)_{16}$ en base $10$.

Une solution

1. On convertit chaque chiffre par sa valeur décimale et on le multiplie par la puissance de $16$ qui correspond au poids de ce chiffre :
   $n = 5 \times 16^2 + 11 \times 16^1 + 2 \times 16^0$ soit $n = 5 \times 256 + 11 \times 16 + 2$.

2. On additionne pour obtenir l'écriture décimale de $n$ : $n = 1458$.

Autre méthode

Puisque la conversion de base $16$ vers base $2$ est facile, de même que la conversion de base $2$ vers base $10$, il est aussi possible d'effectuer une étape par la base $2$ pour convertir un hexadécimal en décimal.

Conversion de décimal à hexadécimal

Pour déterminer l'écriture hexadécimale d'un nombre entier (décimal), deux méthodes sont possibles :

1. Les divisions en cascade en choisissant $16$ comme diviseurs successifs ;

2. Un passage transitoire par la base $2$.

Exemple

Convertir le nombre $n = (51)_{10}$ en base $16$.

Solution avec les divisions successives

1. On pose notre division en cascade:
   

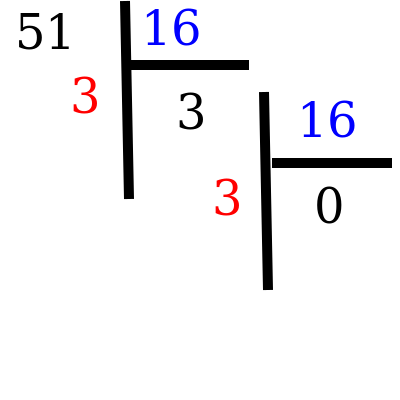
2. L'écriture hexadécimale est donc $(51)_{10} = (33)_{16}$.

3. On peut « vérifier » : $3 \times 16^1 + 3 = 51$.

Solution en passant par la base 2

1. On convertit le nombre $(51)_{10}$ en base $2$ à l'aide d'un tableau listant les puissances de 2 jusqu'à dépasser la valeur de l'entier :

   Puissances de 2	26	25	24	23	22	21	20
   Valeur décimale	64	32	16	8	4	2	1
   Nombre binaire	0	1	1	0	0	1	1

   Ainsi $(51)_{10} = (11 \, 0011)_{2}$.

2. On convertit ensuite ce nombre binaire en groupant les chiffres par paquets de 4 et en convertissant chaque paquet en chiffre hexadécimal à l'aide du tableau de conversion :

   Base 2	0000	0001	0010	0011	0100	0101	0110	0111	1000	1001	1010	1011	1100	1101	1110	1111
   Base 16	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F

   Ainsi $(51)_{10} = (0011 \, 0011)_{2} = (33)_{16}$.