Aller au contenu

TP - Parcours d'arbre binaire☘

Dans le dossier [NSI], créez le dossier [E02-Algo_Arbres].

Téléchargez le module TAD_ArbresBin.py qui contient une implémentation d'arbre binaire et placez ce module dans votre répertoire de travail.

L'interface est celle donnée dans le cours :

Méthode/Opérations Description
A = ArbreBin(rac, fg, fd) Initialisation d'un arbre binaire de racine rac, de fils gauche et fils droit les arbres fg et fd
Ces trois paramètres sont initialisés à None par défaut
est_vide(A) Renvoie True si l'arbre est vide, False sinon.
racine(A) Renvoie la valeur de la racine de l’arbre A si cette racine existe, None sinon.
fils_gauche(A) Renvoie le sous-arbre (fils) gauche de A si ce sous-arbre existe, un arbre vide sinon.
fils_droit(A) Renvoie le sous-arbre (fils) gauche de A si ce sous-arbre existe, un arbre vide sinon.

Attention

Cette interface n'est pas orientée objet, elle s'utilise de la même manière que dans les exemples du cours et dans le TD.

Affichage

Pour visualiser cet arbre, vous avez deux possibilités :

  • La fonction print() réalise un affichage en ligne de l'arbre A passé en argument.
  • La fonction affiche_arbreBin() réalise un affichage en deux dimensions de l'arbre A passé en argument. Cet affichage est effectué à l'aide du module turtle (merci à Q. CHAMUSSY, enseignant dans l'académie de Lyon, pour l'idée originale de cette fonction).

Ce TP a pour but de vous faire programmer les algorithmes de parcours d'arbres binaires étudiés en cours.
Téléchargez le fichier « à trous » : TPE02.10.py (clic droit -> [Enregistrer sous]) et enregistrez-le dans le répertoire de travail.

Partie A - Préparer les arbres de test☘

Afin de tester chacune des fonctions à programmer dans ce TP et vous familiariser avec l'interface, programmez les trois arbres ci-dessous dans le « main » de votre programme.
Affichez chaque arbre afin de vérifier votre travail.

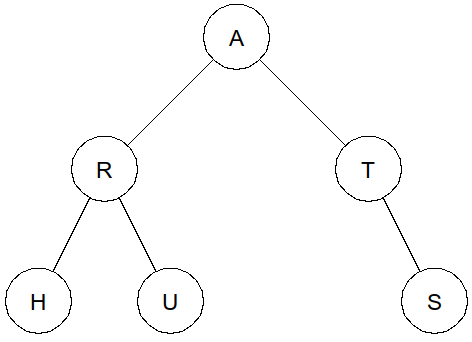
  1. Arbre n°1 Premier arbre

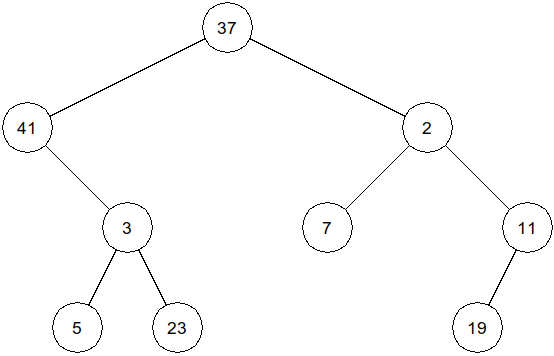
  2. Arbre n°2 Premier arbre

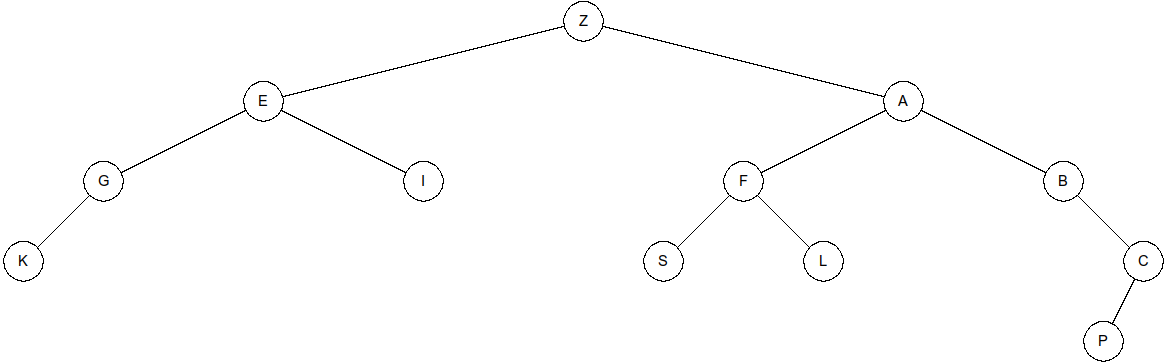
  3. Arbre n°3 Premier arbre

Partie B - Parcours en profondeur☘

  1. Complétez la définition récursive de la fonction parcours_infixe() qui prend en paramètre un arbre binaire et une variable tab initialisée à None. Cette fonction renvoie le tableau tab contenant les nœuds de l'arbre visités dans l'ordre infixe.

    1
2
3
4
5
6
7
    def parcours_infixe(arbre, tab=None):
    """
    arbre - ArbreBin, arbre binaire
    tab - list, tableau contenant des noeuds de l'arbre
    Sortie: list, tableau tab contenant les noeuds de l'arbre parcourus
            en ordre infixe (fils gauche, noeud, fils droit)
    """

    Plan de test

    >>> parcours_infixe(arbre1)
['H', 'R', 'U', 'A', 'T', 'S']

>>> parcours_infixe(arbre2)
[41, 5, 3, 23, 37, 7, 2, 19, 11]

>>> parcours_infixe(arbre3)
['K', 'G', 'E', 'I', 'Z', 'S', 'F', 'L', 'A', 'B', 'P', 'C']
    Une piste

    La variable tab est initialisée par défaut à None.
    Il faut tester cette situation et « placer » alors un tableau vide dans cette variable.

  2. Complétez la définition récursive de la fonction parcours_prefixe() qui prend en paramètre un arbre binaire et une variable tab initialisée à None. Cette fonction renvoie le tableau tab contenant les nœuds de l'arbre visités dans l'ordre préfixe.

    1
2
3
4
5
6
7
    def parcours_prefixe(arbre, tab=None):
    """
    arbre - ArbreBin, arbre binaire
    tab - list, tableau contenant des noeuds de l'arbre
    Sortie: list, tableau tab contenant les noeuds de l'arbre parcourus
            en ordre prefixe (noeud, fils gauche, fils droit)
    """

    Plan de test

    >>> parcours_prefixe(arbre1)
['A', 'R', 'H', 'U', 'T', 'S']

>>> parcours_prefixe(arbre2)
[37, 41, 3, 5, 23, 2, 7, 11, 19]

>>> parcours_prefixe(arbre3)
['Z', 'E', 'G', 'K', 'I', 'A', 'F', 'S', 'L', 'B', 'C', 'P']
    Une piste

    La variable tab est initialisée par défaut à None.
    Il faut tester cette situation et « placer » alors un tableau vide dans cette variable.

  3. Complétez la définition récursive de la fonction parcours_suffixe() qui prend en paramètre un arbre binaire et une variable tab initialisée à None. Cette fonction renvoie le tableau tab contenant les nœuds de l'arbre visités dans l'ordre suffixe.

    1
2
3
4
5
6
7
    def parcours_suffixe(arbre, tab=None):
    """
    arbre - ArbreBin, arbre binaire
    tab - list, tableau contenant des noeuds de l'arbre
    Sortie: list, tableau tab contenant les noeuds de l'arbre parcourus
            en ordre suffixe (fils gauche, fils droit, noeud)
    """

    Plan de test

    >>> parcours_suffixe(arbre1)
['H', 'U', 'R', 'S', 'T', 'A']

>>> parcours_suffixe(arbre2)
[5, 23, 3, 41, 7, 19, 11, 2, 37]

>>> parcours_suffixe(arbre3)
['K', 'G', 'I', 'E', 'S', 'L', 'F', 'P', 'C', 'B', 'A', 'Z']
    Une piste

    La variable tab est initialisée par défaut à None.
    Il faut tester cette situation et « placer » alors un tableau vide dans cette variable.

Partie C - Parcours en largeur☘

Complétez la définition itérative de la fonction parcours_largeur() qui prend en paramètre un arbre binaire et qui renvoie un tableau contenant les nœuds de l'arbre visités « en largeur ».

1
2
3
4
5
6
def parcours_largeur(arbre):
    """
    arbre - ArbreBin, arbre binaire
    Sortie: list, tableau contenant les noeuds de l'arbre
            parcourus en largeur
    """

Plan de test

>>> parcours_largeur(arbre1)
['A', 'R', 'T', 'H', 'U', 'S']

>>> parcours_largeur(arbre2)
[37, 41, 2, 3, 7, 11, 5, 23, 19]

>>> parcours_largeur(arbre3)
['Z', 'E', 'A', 'G', 'I', 'F', 'B', 'K', 'S', 'L', 'C', 'P']
Une piste

Pour programmer ce parcours, vous avez besoin d'utiliser une file.

  • Soit vous utilisez une structure de file programmée plus tôt dans l'année.
  • Soit vous utilisez un tableau (liste Python) comme une file dont le premier élément est l'élément d'indice 0 (défilé avec .pop(0)) et le dernier élément est enfilé en fin de tableau (méthode .append()).

Partie D - Parcours itératifs en profondeur☘

  1. Complétez la définition itérative de la fonction parcours_prefixe_iter() qui prend en paramètre un arbre binaire et renvoie un tableau contenant les nœuds de l'arbre visités dans l'ordre préfixe.

    1
2
3
4
5
6
7
    def parcours_prefixe_iter(arbre):
    """
    arbre - ArbreBin, arbre binaire
    Sortie: list, tableau contenant les noeuds de l'arbre parcourus
            en ordre prefixe (noeud, fils gauche, fils droit)
            (méthode itérative)
    """

    Plan de test

    >>> parcours_prefixe_iter(arbre1)
['A', 'R', 'H', 'U', 'T', 'S']

>>> parcours_prefixe_iter(arbre2)
[37, 41, 3, 5, 23, 2, 7, 11, 19]

>>> parcours_prefixe_iter(arbre3)
['Z', 'E', 'G', 'K', 'I', 'A', 'F', 'S', 'L', 'B', 'C', 'P']
    Une piste

    Pour programmer ce parcours, vous avez besoin d'utiliser une pile.

    • Soit vous utilisez une structure de pile programmée plus tôt dans l'année.
    • Soit vous utilisez un tableau (liste Python) comme une pile dont le dernier élément est le sommet de la pile (dépilé avec .pop(), empilé avec .append()).
    Un algorithme
    1. Placer l'arbre dans la pile.
    2. On dépile cet arbre, on place sa racine dans le tableau, on empile le sous-arbre droit puis le sous-arbre gauche (s'ils existent).
    3. On recommence jusqu'à ce que la pile soit vide...

  2. Complétez la définition itérative de la fonction parcours_suffixe_iter() qui prend en paramètre un arbre binaire et renvoie un tableau contenant les nœuds de l'arbre visités dans l'ordre suffixe.

    1
2
3
4
5
6
7
    def parcours_suffixe_iter(arbre):
    """
    arbre - ArbreBin, arbre binaire
    Sortie: list, tableau contenant les noeuds de l'arbre parcourus
            en ordre suffixe (fils gauche, fils droit, noeud)
            (méthode itérative)
    """

    Plan de test

    >>> parcours_suffixe_iter(arbre1)
['H', 'U', 'R', 'S', 'T', 'A']

>>> parcours_suffixe_iter(arbre2)
[5, 23, 3, 41, 7, 19, 11, 2, 37]

>>> parcours_suffixe_iter(arbre3)
['K', 'G', 'I', 'E', 'S', 'L', 'F', 'P', 'C', 'B', 'A', 'Z']
    Une piste

    Pour programmer ce parcours, vous avez besoin d'utiliser une pile.

    • Soit vous utilisez une structure de pile programmée plus tôt dans l'année.
    • Soit vous utilisez un tableau (liste Python) comme une pile dont le dernier élément est le sommet de la pile (dépilé avec .pop(), empilé avec .append()).
    Un algorithme

    C'est presque le même algorithme que celui de la fonction précédente, mis à part qu'on place le nouveau nœud parcouru au début du tableau de parcours.