Aller au contenu

Exercices pour s'entraîner sur les parcours d'arbre☘

Prenez l'habitude de revenir vous entraîner régulièrement avec ces exercices tout au long de l'année. Ils sont généralement accompagnés de pistes et de leur solution pour vous permettre de progresser.

Rappels

  • Chaque programme Python doit être sauvegardé sous forme de fichier texte avec l'extension .py.
    Enregistrez ce fichier dans le dossier [E02-Algo_Arbres] avec le nom donné à l'exercice : ProgE02.51.py, ProgE02.52.py, etc...
  • Pour exécuter ce programme, il suffit de le sauvegarder puis d'appuyer sur la touche [F5].

Préambule☘

Téléchargez le module TAD_ArbresBin.py qui contient une implémentation d'arbre binaire et placez ce module dans votre répertoire de travail.

L'interface est celle donnée dans le cours :

Méthode/Opérations Description
A = ArbreBin(rac, fg, fd) Initialisation d'un arbre binaire de racine rac, de fils gauche et fils droit les arbres fg et fd
Ces trois paramètres sont initialisés à None par défaut
est_vide(A) Renvoie True si l'arbre est vide, False sinon.
racine(A) Renvoie la valeur de la racine de l’arbre A si cette racine existe, None sinon.
fils_gauche(A) Renvoie le sous-arbre (fils) gauche de A si ce sous-arbre existe, un arbre vide sinon.
fils_droit(A) Renvoie le sous-arbre (fils) gauche de A si ce sous-arbre existe, un arbre vide sinon.

Attention

Cette interface n'est pas orientée objet, elle s'utilise de la même manière que dans les exemples du cours et dans le TD.

Affichage

Pour visualiser cet arbre, vous avez deux possibilités :

  • La fonction print() réalise un affichage en ligne de l'arbre A passé en argument.
  • La fonction affiche_arbreBin() réalise un affichage en deux dimensions de l'arbre A passé en argument. Cet affichage est effectué à l'aide du module turtle (merci à Q. CHAMUSSY, enseignant dans l'académie de Lyon, pour l'idée originale de cette fonction).

ProgE02.51 - Arbre binaire parfait☘

Complétez la définition récursive de la fonction creer_arbre_parfait() qui prend en paramètres un entier strictement positif hauteur et qui renvoie un arbre binaire parfait de hauteur hauteur dont les nœuds sont numérotés de 1 à 2hauteur-1.

1
2
3
4
5
6
7
8
def creer_arbre_parfait(hauteur, niv=1, etiquette=1):
    """
    hauteur - int, entier strictement positif
    niv - int, entier tel que 0 < niv <= hauteur
    etiquette - int, numéro du noeud (de 1 pour la racine à 2**hauteur - 1)
    Sortie: ArbreBin - Arbre binaire parfait de hauteur hauteur et dont les
            noeuds sont numérotés de 1 pour la racine à 2**hauteur - 1
    """

Exemple

>>> arbre_parfait = creer_arbre_parfait(4)

>>> affiche_arbreBin(arbre_parfait)
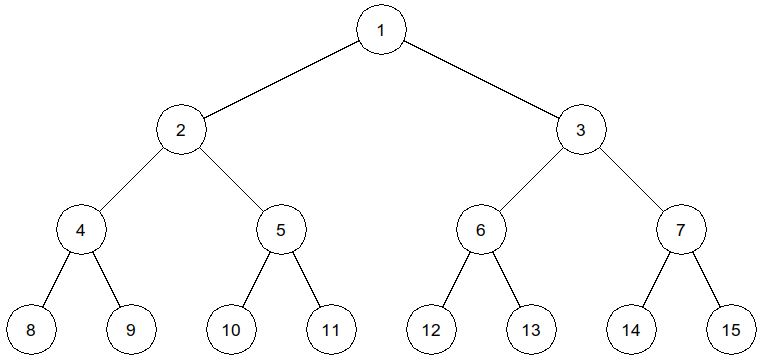
arbre

Une solution
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
def creer_arbre_parfait(hauteur, niv=1, etiquette=1):
    """
    hauteur - int, entier strictement positif
    niv - int, entier tel que 0 < niv <= hauteur
    etiquette - int, numéro du noeud (de 1 pour la racine à 2**hauteur - 1)
    Sortie: ArbreBin - Arbre binaire parfait de hauteur hauteur et dont les
            noeuds sont numérotés de 1 pour la racine à 2**hauteur - 1
    """
    if niv <= hauteur:
        return ArbreBin(etiquette,
                        creer_arbre_parfait(hauteur, niv+1, etiquette*2),
                        creer_arbre_parfait(hauteur, niv+1, etiquette*2+1))

ProgE02.52 - Opérations arithmétiques☘

Cet exercice a été adapté d'un travail réalisé par C. BLANCHER et M. CHARDET, enseignants en informatique.

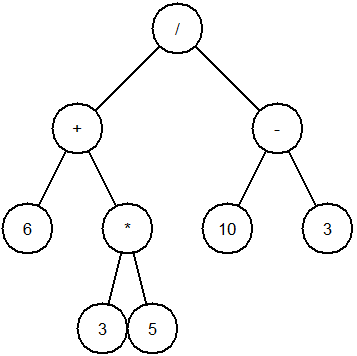Arbre formule Dans cet exercice, on considère des arbres binaires qui représentent des opérations arithmétiques avec les quatre opérateurs usuels : +, -, \* et /.

L'exemple ci-contre correspond à l'expression (6+(3\*5))/(10-3).

Dans le fichier à trous fourni, ces arbres sont représentés par une classe ArbreFormule avec trois attributs :

  • racine :
    • si la racine de l'arbre est une opération, chaîne de caractère ('+', '-', '*' ou '/') correspondante à l'opération ;
    • si la racine de l'arbre est une feuille (et donc un nombre), contient ce nombre (de type int ou float).
  • filsG :
    • si la racine de l'arbre est une opération, contient le sous-arbre gauche ;
    • si la racine de l'arbre est une feuille, contient None.
  • filsD :
    • si la racine de l'arbre est une opération, contient le sous-arbre droit ;
    • si la racine de l'arbre est une feuille, contient None.

On cherche à afficher un arbre sous deux formes différentes, et à calculer le résultat de l'opération qu'il représente.

La méthode est_operation(), déjà programmée, permet de savoir si la racine de l'arbre est une opération ou un nombre. Elle renvoie True si le noeud représente une opération (c'est-à-dire n'est pas une feuille) et renvoie False si le noeud représente un nombre (c'est-à-dire est une feuille).

Rappel

Pour afficher du texte dans la console sans faire de retour à la ligne, il faut fournir un argument supplémentaire à la fonction print().
Par exemple :

1
2
print("Bonjour, ", end="")
print("comment ça va ?")

En exécutant les lignes ci-dessus, on obtient l'affichage suivant dans la console, sans retour à la ligne entre les deux : 

>>> 
"Bonjour, comment ça va ?"

  1. Compléter la définition de la méthode récursive afficher_fonction() et indiquer en commentaire le type de parcours d'arbre correspondant :

    1
2
3
4
5
6
7
    def afficher_fonction(self):
    """
    Affiche la formule représentée par l'arbre sous forme fonctionnelle.
    Par exemple : div(add(6, mul(3, 5)), sub(10, 3))
    Renvoie None (fonction d'affichage).
    """
    pass
    Une solution

    On effectue un parcours préfixe de l'arbre. 

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
    def afficher_fonction(self):
    """
    Affiche la formule représentée par l'arbre sous forme fonctionnelle.
    Par exemple : div(add(6, mul(3, 5)), sub(10, 3))
    Renvoie None (fonction d'affichage).
    """

    if not self.est_operation():
        print(self.racine, end="")
    else:
        if self.racine == "+":
            print("add", end="")
        elif self.racine == "-":
            print("sub", end="")
        elif self.racine == "*":
            print("mul", end="")
        elif self.racine == "/":
            print("div", end="")
        else:
            assert False, "Opération inexistante"

        print("(", end="")
        self.filsG.afficher_fonction()
        print(", ", end="")
        self.filsD.afficher_fonction()
        print(")", end="")

  2. Compléter la définition de la méthode récursive afficher_maths() et indiquer en commentaire le type de parcours d'arbre correspondant :

    1
2
3
4
5
6
7
    def afficher_maths(self):
    """
    Affiche la formule représentée par l'arbre sous forme mathématique.
    Par exemple : ((6+(3*5))/(10-3))
    Renvoie None (fonction d'affichage).
    """
    pass
    Une solution

    On effectue un parcours infixe de l'arbre. 

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
    def afficher_maths(self):
    """
    Affiche la formule représentée par l'arbre sous forme mathématique.
    Par exemple : ((6+(3*5))/(10-3))
    Renvoie None (fonction d'affichage).
    """

    if not self.est_operation():
        print(self.racine, end="")
    else:
        print("(", end="")
        self.filsG.afficher_maths()

        print(self.racine, end="")

        self.filsD.afficher_maths()
        print(")", end="")

  3. Compléter la définition de la méthode récursive calculer() et indiquer en commentaire le type de parcours d'arbre correspondant :

    1
2
3
4
5
6
7
    def calculer(self):
    """
    Calcule le résultat de la formule représentée par l'arbre.
    Vérifie par une assertion qu'il n'y a pas de division par 0.
    Renvoie le résultat du calcul.
    """
    pass
    Une solution

    On effectue un parcours suffixe de l'arbre. 

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
    def calculer(self):
    """
    Calcule le résultat de la formule représentée par l'arbre.
    Vérifie par une assertion qu'il n'y a pas de division par 0.
    Renvoie le résultat du calcul.
    """

    if not self.est_operation():
        return self.racine
    else:
        valeurG = self.filsG.calculer()
        valeurD = self.filsD.calculer()

        if self.racine == "+":
            return valeurG+valeurD
        elif self.racine == "-":
            return valeurG-valeurD
        elif self.racine == "*":
            return valeurG*valeurD
        elif self.racine == "/":
            assert valeurD != 0, "Division par 0 !"
            return valeurG/valeurD
        else:
            assert False, "Opération inexistante"

ProgE02.53 - Arbre le plus proche☘

Dans cet exercice, on considère un arbre qui représente une carte routière. Vous pouvez télécharger le fichier à compléter en cliquant ici.

Chaque noeud de l'arbre correspond à un emplacement qui a un nom (un identifiant self.nom). Chaque emplacement peut aussi être une aire de repos (auquel cas le booléen self.repos vaut True).

Les arêtes de l'arbre correspondent à des routes menant d'un emplacement à un autre. Les sous-arbres gauche et droit (self.filsG et self.filsD) contiennent soit un emplacement vers lequel on peut se diriger, soit None.

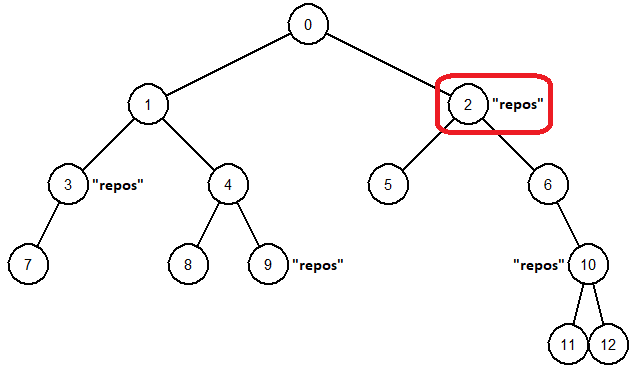
Exemple de parcours en largeur

La racine de l'arbre représente notre position. Comme nous sommes très fatigués, nous cherchons l'aire de repos la plus proche. Dans l'exemple ci-dessus, cela correspond au noeud 2.

  1. Quel type de parcours est approprié pour trouver l'aire de repos la plus proche de la racine ?

    Une solution

    Un parcours en largeur de l'arbre semble approprié.

  2. Compléter la définition de la méthode non-récursive repos_plus_proche() en respectant ses spécifications.

    1
2
3
4
5
6
7
8
    def repos_plus_proche(self):
    """
    Renvoie le nom du noeud de l'arbre le plus proche ayant une aire de
    repos (attribut `repos` = True). Si aucun élément de l'arbre ne
    correspond, renvoie None.
    """
    a_explorer = [self]  # On met le noeud courant (self) dans la file de noeuds à explorer
    pass

    Résultats attendus

    Le programme teste avec quatre versions différentes d'un arbre.
    L'affichage attendu dans la console est le suivant : 

    2
3
10
0
Programme correct !

    Un premier indice

    a_explorer est une file de noeuds de l'arbre à explorer dans l'ordre d'ajout.
    Tant que cette file n'est pas vide, on continue l'exploration, en commençant par le premier noeud.

    Un second indice

    L'exploration d'un noeud peut mener à ajouter des éléments à la file a_explorer.

    Une solution
     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
    def repos_plus_proche(self):
    """
    Renvoie le nom du noeud de l'arbre le plus proche ayant une aire de
    repos (attribut `repos` = True). Si aucun élément de l'arbre ne
    correspond, renvoie None.
    """
    a_explorer = [self]  # On met le noeud courant (self) dans la file de noeuds à explorer
    while len(a_explorer) > 0:
        element = a_explorer.pop(0)
        if element.repos:
            return element.nom
        if element.filsG is not None:
            a_explorer.append(element.filsG)
        if element.filsD is not None:
            a_explorer.append(element.filsD)
    return None

ProgE02.54 - Reconstruire un arbre à partir de deux parcours☘

Nous avons vu en TD qu'il était possible de reconstruire un arbre binaire à partir de la donnée de deux de ses parcours. Cet exercice a pour but d'automatiser la méthode étudiée en classe dans le cas où tous les noeuds de l'arbre contiennent des valeurs distinctes.

  1. Copiez/collez complétez la définition de la fonction partage() qui prend en paramètre un tableau dont tous les éléments sont distincts et une valeur contenue dans ce tableau. Cette fonction renvoie un couple de tableaux tel que décrit dans la spécification.

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
    def partage(tab, valeur):
    """
    tab - list, tableau d'éléments tous distincts
    valeur - un élément du tableau
    Sortie: tuple - couple de tableaux
            Le premier est constitué des éléments de tab jusqu'à valeur
            Le second est constitué des éléments de tab à partir de valeur
    >>> tab = [3, 2, 1, 4, 5, 8, 6, 7]
    >>> partage(tab, 4)
    ([3, 2, 1], [5, 8, 6, 7])
    """
    Une solution
     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
    def partage(tab, valeur):
    """
    tab - list, tableau d'éléments tous distincts
    valeur - un élément du tableau
    Sortie: tuple - couple de tableaux
            Le premier est constitué des éléments de tab jusqu'à valeur
            Le second est constitué des éléments de tab à partir de valeur
    >>> tab = [3, 2, 1, 4, 5, 8, 6, 7]
    >>> partage(tab, 4)
    ([3, 2, 1], [5, 8, 6, 7])
    """
    tab1 = []
    tab2 = []
    i = 0
    while tab[i] != valeur:
        tab1.append(tab[i])
        i += 1
    for k in range(i+1, len(tab)):
        tab2.append(tab[k])
    return tab1, tab2

  2. Copiez/collez complétez la définition récursive de la fonction construire_arbre() qui prend en paramètres deux tableaux. Le premier correspond au parcours infixe d'un arbre binaire, le second au parcours suffixe du même arbre.
    Cette fonction renvoie l'arbre binaire dont les parcours ont été donnés (objet de type ArbreBin - importez le module TAD_ArbresBin.py).

    1
2
3
4
5
6
    def construire_arbre(infixe, suffixe):
    """
    infixe - list, parcours infixe d'un arbre binaire
    suffixe - list, parcours suffixe du MÊME arbre binaire
    Sortie: ArbreBin - l'arbre binaire dont les parcours ont été donnés
    """

    Exemples

    >>> infixe = [3, 2, 1, 4, 5, 8, 6, 7]
>>> suffixe = [3, 1, 2, 5, 6, 8, 7, 4]
>>> arbre = construire_arbre(infixe, suffixe)
>>> affiche_arbreBin(arbre)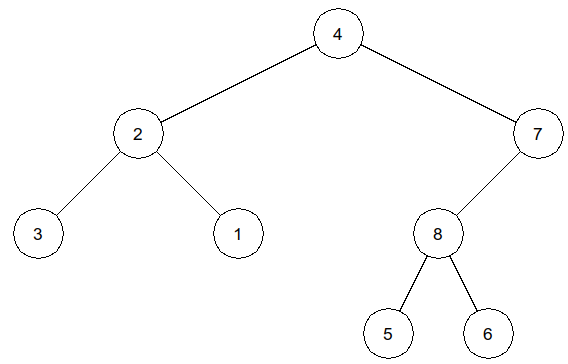
    arbre

    Une piste
    1. Identifier les cas de base ;
    2. Sortir la racine du parcours suffixe ;
    3. Partager le parcours infixe en deux ;
    4. En déduire les deux sous-tableaux suffixe correspondant ;
    5. Construire un arbre à partir de la racine et des deux sous-arbres construis à partir des sous-tableaux.
    Une solution
     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
    def construire_arbre(infixe, suffixe):
    """
    infixe - list, parcours infixe d'un arbre binaire
    suffixe - list, parcours suffixe du MÊME arbre binaire
    Sortie: ArbreBin - l'arbre binaire dont les parcours ont été donnés
    """
    if len(suffixe) == 0:
        return None
    elif len(suffixe) == 1:
        return ArbreBin(suffixe[0])
    else:
        racine = suffixe.pop()
        infixe1, infixe2 = partage(infixe, racine)
        n1, n2 = len(infixe1), len(infixe2)

        suffixe1, suffixe2 = [], []
        for i in range(n1):
            suffixe1.append(suffixe[i])

        for k in range(n2):
            suffixe2.append(suffixe[n1+k])
        return ArbreBin(racine,
                        construire_arbre(infixe1, suffixe1),
                        construire_arbre(infixe2, suffixe2))

  3. Copiez/collez complétez la définition récursive de la fonction construire_arbre2() qui prend en paramètres deux tableaux. Le premier correspond au parcours infixe d'un arbre binaire, le second au parcours prefixe du même arbre.
    Cette fonction renvoie l'arbre binaire dont les parcours ont été donnés (objet de type ArbreBin - importez le module TAD_ArbresBin.py).

    1
2
3
4
5
6
    def construire_arbre2(infixe, prefixe):
    """
    infixe - list, parcours infixe d'un arbre binaire
    prefixe - list, parcours préfixe du MÊME arbre binaire
    Sortie: ArbreBin - l'arbre binaire dont les parcours ont été donnés
    """

    Exemples

    >>> infixe = [1, 3, 4, 5, 2, 6, 7, 8]
>>> prefixe = [6, 3, 1, 5, 4, 2, 7, 8]
>>> arbre2 = construire_arbre2(infixe, prefixe)
>>> affiche_arbreBin(arbre2)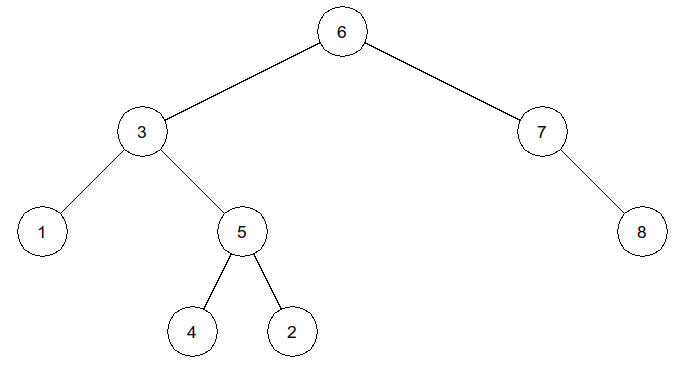
    arbre

    Une piste

    Même principe que la fonction précédente.

    Une solution
     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
    def construire_arbre2(infixe, prefixe):
    """
    infixe - list, parcours infixe d'un arbre binaire
    prefixe - list, parcours préfixe du MÊME arbre binaire
    Sortie: ArbreBin - l'arbre binaire dont les parcours ont été donnés
    """
    if len(prefixe) == 0:
        return None
    elif len(prefixe) == 1:
        return ArbreBin(prefixe[0])
    else:
        racine = prefixe.pop(0)
        infixe1, infixe2 = partage(infixe, racine)
        n1, n2 = len(infixe1), len(infixe2)

        prefixe1, prefixe2 = [], []
        for i in range(n1):
            prefixe1.append(prefixe[i])

        for k in range(n2):
            prefixe2.append(prefixe[n1+k])
        return ArbreBin(racine,
                        construire_arbre2(infixe1, prefixe1),
                        construire_arbre2(infixe2, prefixe2))