Aller au contenu

TP - Arbres Binaires de Recherche☘

Ce TP doit conduire à créer de A à Z un module utilisable tout le reste de l'année.

Téléchargez le fichier « à trous » TAD_ABR.py (clic droit -> [Enregistrer la cible du lien sous]) et enregistrez-le dans le dossier intitulé [Mes_modules].

Ce TP a pour but de définir une structure de données implémentant des arbres binaires de recherche muables en programmation orientée objet.

Remarque importante

La partie A va permettre d'implémenter une classe ArbreBinR dont l'interface sera celle d'un arbre binaire usuel, à laquelle on ajoute l'insertion d'un élément.
La partie B va compléter cette implémentation par de nouvelles méthodes, ce qui pourra permettre de modifier l'interface.

Partie A - Classe ArbreBinR☘

Les objets de la classe ArbreBinR sont munis de trois attributs : noeud, fg et fd initialisés à None par défaut. Lors de l'initialisation d'un arbre binaire de recherche, il ne doit pas être possible de spécifier ses sous-arbres gauche et/ou droit.

Remarque

On a muni cette classe d'une méthode affichage() déjà programmée qui permet d'ores et déjà d'afficher l'arbre à l'aide du module turtle.
Il ne faut surtout pas chercher à modifier cette méthode.

Complétez les méthodes de cette classe et vérifiez votre travail à l'aide du plan de test qui suit.

On définit un arbre « à la main » : 

1
2
3
4
5
6
7
8
if __name__ == "__main__":
    arbre1 = ArbreBinR()
    arbre1.inserer(5)
    arbre1.inserer(1)
    arbre1.inserer(6)
    arbre1.inserer(2)
    arbre1.inserer(7)
    arbre1.inserer(8)

Puis on teste dans la console : 

>>> arbre1
(5, (1, (), (2, (), ())), (6, (), (7, (), (8, (), ()))))

>>> arbre1.racine()
5

>>> arbre1.est_vide()
False

>>> arbre1.est_feuille()
False

>>> arbre1.fils_gauche()
(1, (), (2, (), ()))

>>> arbre1.fils_droit()
(6, (), (7, (), (8, (), ())))
False

>>> arbre1.fils_gauche().inserer(4)

>>> arbre1.fils_gauche()
(1, (), (2, (), (4, (), ())))

>>> arbre1.affichage()
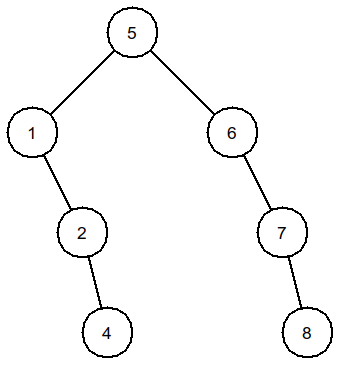
arbre_exemple

Lorsque l'arbre est vide, on « initialise » cet arbre en donnant une valeur à sa racine (son nœud) et en initialisant les fils gauche et droite comme des arbres vides.

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
# Structure d'arbre binaire de recherche en POO
# Idée originale pour l'affichage : Q. CHAMUSSY

from turtle import *
from random import randint

class ArbreBinR():
    """
    Implémentation d'arbres binaires de recherche
    """

    def __init__(self):
        """
        Initialisation d'un arbre binaire (de recherche)
        """
        self.noeud = None       
        self.fg = None
        self.fd = None


    def est_vide(self):
        """
        Sortie: bool - lien True si l'arbre binaire de recherche est vide,
                False sinon
        """
        pass


    def inserer(self, valeur):
        """
        valeur - élément de même type que les autres valeurs de l'ArbreBinR
        Sortie: None - l'arbre dans lequel valeur a été insérée au bon endroit
                Lorsque l'arbre est vide, valeur remplace le nœud et les deux
                fils sont remplacés par des arbres vides.
        """
        pass


    def est_feuille(self):
        """
        Sortie: bool - True si l'arbre binaire de recherche est réduit
                à une feuille, False sinon
        """
        pass


    def racine(self):
        """
        Sortie: elt - valeur de la racine, éventuellement None
        """
        pass


    def fils_gauche(self):
        """
        Sortie: ArbreBinR - lien vers le fils gauche (soit un ArbreBinR,
                soit None lorsque l'arbre est vide)
                Attention aux effets de bord
        """
        pass


    def fils_droit(self):
        """
        Sortie: ArbreBinR - lien vers le fils droit (soit un ArbreBinR,
                soit None lorsque l'arbre est vide)
                Attention aux effets de bord
        """
        pass


    def __repr__(self):
        """
        Sortie: str - Chaîne d'affichage de l'arbre binaire de recherche "en ligne"
        """
        pass


    def affichage(self, couleur_trace="black", couleur_fond="white"):
        """
        NE RIEN MODIFIER DANS CETTE MÉTHODE !
        Affichage turtle de l'arbre binaire de recherche.
        Si l'arbre est vide, ne fait rien
        """
        def hauteur(arbre = self):
            """
            Sortie: int - hauteur de l'arbre
                    (0 pour l'arbre vide, 1 pour un arbre réduit à une feuille)
            """
            if arbre.est_vide():
                return 0
            elif arbre.est_feuille():
                return 1
            elif arbre.fg.est_vide():
                return 1+hauteur(arbre.fd)
            elif arbre.fd.est_vide():
                return 1+hauteur(arbre.fg)
            else:
                return 1+max(hauteur(arbre.fg), hauteur(arbre.fd))

        def aller(x, y):
            """positionnne la tortue en x, y sans tracer."""
            up()
            goto(x, y)
            down()

        def cercle(x, y, r):
            """trace un cercle de centre (x;y) et de rayon r.
            Le cercle est par défaut en noir sur fond blanc."""
            aller(x, y - r)
            color(couleur_trace, couleur_fond)
            begin_fill()
            circle(r)
            end_fill()
            aller(x, y)

        def ecrit(x, y, legende, taille_police):
            """écrite le texte de légende au centre du noeud (du cercle)"""
            aller(x + 1, y - taille_police + 2)
            if isinstance(legende, tuple):
                if legende[0] is None:
                    legende = str(legende[1])
                else:
                    legende = str(legende[0]) + str(legende[1])
            else:
                legende = str(legende)
            write(f"{legende}", align = "center", font = ("Arial", taille_police, "normal")) # affichage de l'étiquette
            aller(x, y)

        def trace(n, arbre = self, x = 0, y = 300):
            """trace récursivement l'arbre avec la tortue"""
            if n > 0 and not arbre.est_vide():
                goto(x, y)                              # branche de l'arbre
                gauche = (x - 2**(n-2) * d, y - 4*d)    # position du prochain noeud gauche
                droit = (x + 2**(n-2) * d, y - 4*d)     # position du prochain noeud droit
                trace(n - 1, arbre.fg, *gauche)         # appel récursif gauche
                aller(x, y)                             # retour au noeud
                trace(n - 1, arbre.fd, *droit)          # appel récursif droit
                aller(x, y)                             # retour au noeud
                cercle(x, y, d)                         # tracé du noeud
                ecrit(x, y, arbre.noeud, taille_police)

        if not self.est_vide():         # Constantes et paramètres
            TurtleScreen._RUNNING = True
            p = hauteur()               # Nombre de niveaux
            d = 100//p                  # rayon d'une étiquette
            speed(0)
            hideturtle()
            width(2)                    # épaisseur de 2 du crayon

            taille_police = 1 + d//2    # calcul de la taille de la police
            aller(0, 300)               # position de départ
            trace(p)                    # appel de la fonction de tracé
            exitonclick()

Partie B - Interface améliorée☘

Dans cette partie, il va falloir reprogrammer une partie des fonctions déjà étudiées dans le premier TP sous une forme « orientée objet ».

Conseil général

N'oubliez pas de gérer le fait que les fils peuvent être vides...

  1. Copiez, collez et complétez la définition de la méthode insere_tab() qui prend en paramètre un tableau d'éléments comparables et qui remplit l'arbre binaire de recherche de ces éléments.

    1
2
3
4
5
6
    def insere_tab(self, tab):
    """
    tab - list, tableau de valeurs de même type que les noeuds
          de l'arbre binaire de recherche
    Sortie: None - l'arbre dans lequel valeur a été insérée au bon endroit
    """

    Plan de test

    >>> arbre2 = ArbreBinR()
>>> arbre2.insere_tab([11, 14, 12, 13, 7, 10, 5, 17])
>>> arbre2.affichage()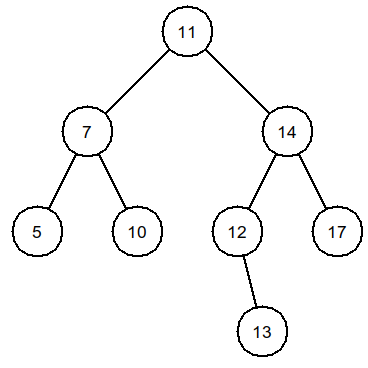
    arbre_exemple

  2. Définissez la méthode mini() qui renvoie la valeur du plus petit noeud de l'arbre (None pour un arbre vide).

    Plan de test

    >>> arbre1.mini()
1

>>> arbre2.mini()
5

  3. Définissez la méthode maxi() qui renvoie la valeur du plus grand noeud de l'arbre (None pour un arbre vide).

    Plan de test

    >>> arbre1.maxi()
8

>>> arbre2.maxi()
17

  4. Copiez, collez et complétez la définition de la méthode recherche() qui prend en paramètre un élément de même type que celui des nœuds de l'arbre et qui renvoie True si cet élément est présent dans l'arbre, False sinon.

    1
2
3
4
5
    def recherche(self, valeur):
    """
    valeur - élément de même type que les autres valeurs de l'ArbreBinR
    Sortie: bool - True si valeur est dans l'arbre, False sinon
    """

    Plan de test

    >>> arbre1.recherche(6)
True

>>> arbre2.recherche(6)
False

  5. Programmez les méthodes suivantes :

    a. parcours_largeur() qui renvoie le tableau (éventuellement vide) des nœuds de l'arbre binaire de recherche parcourus en largeur ;
    b. parcours_prefixe() qui renvoie le tableau (éventuellement vide) des nœuds de l'arbre binaire de recherche parcourus en ordre préfixe ;
    c. parcours_infixe() qui renvoie le tableau (éventuellement vide) des nœuds de l'arbre binaire de recherche parcourus en ordre infixe ;
    d. parcours_suffixe() qui renvoie le tableau (éventuellement vide) des nœuds de l'arbre binaire de recherche parcourus en ordre suffixe ;

  6. Dans le « main », programmez la fonction tri_ABR() qui prend en paramètre un tableau d'éléments comparables et qui renvoie un tableau contenant les mêmes éléments mais triés dans l'ordre croissant.
    Cette fonction doit utiliser un arbre binaire de recherche pour effectuer ce tri.

    1
2
3
4
5
6
7
    def tri_ABR(tab):
    """
    tab - list, tableau d'éléments comparables
    Sortie: list - tableau contenant les mêmes éléments
            mais triés dans l'ordre croissant en utilisant
            un arbre binaire de recherche intermédiaire.
    """

    Plan de test

    >>> tab = [5, 1, 6, 2, 7, 8, 4]     
>>> tri_ABR(tab)
[1, 2, 4, 5, 6, 7, 8]