Exercices pour s'entraîner sur les ABR☘
Prenez l'habitude de revenir vous entraîner régulièrement avec ces exercices tout au long de l'année. Ils sont généralement accompagnés de pistes et de leur solution pour vous permettre de progresser.
Rappels
- Chaque programme Python doit être sauvegardé sous forme de fichier texte
avec l'extension
.py.
Enregistrez ce fichier dans le dossier[E02-Algo_Arbres]avec le nom donné à l'exercice :ProgE02.61.py,ProgE02.62.py, etc... - Pour exécuter ce programme, il suffit de le sauvegarder puis d'appuyer
sur la touche
[F5].
ProgE02.61 - Arbre binaire de recherche ?☘
-
Téléchargez le module TAD_ArbresBin.py qui contient une implémentation d'arbre binaire et placez ce module dans votre répertoire de travail.
L'interface est celle donnée dans le cours.Rappels
Méthode/Opérations Description A = ArbreBin(rac, fg, fd)Initialisation d'un arbre binaire de racine rac, de fils gauche et fils droit les arbresfgetfd. Ces trois paramètres sont initialisés àNonepar défautest_vide(A)Renvoie Truesi l'arbre est vide,Falsesinon.racine(A)Renvoie la valeur de la racine de l’arbre Asi cette racine existe,Nonesinon.fils_gauche(A)Renvoie le sous-arbre (fils) gauche de Asi ce sous-arbre existe, un arbre vide sinon.fils_droit(A)Renvoie le sous-arbre (fils) gauche de Asi ce sous-arbre existe, un arbre vide sinon.Attention
Cette interface n'est pas orientée objet, elle s'utilise de la même manière que dans les exemples du cours et dans le TD.
Affichage
Pour visualiser cet arbre, vous avez deux possibilités :
- La fonction
print()réalise un affichage en ligne de l'arbre A passé en argument. - La fonction
affiche_arbreBin()réalise un affichage en deux dimensions de l'arbre A passé en argument. Cet affichage est effectué à l'aide du moduleturtle(merci à Q. CHAMUSSY, enseignant dans l'académie de Lyon, pour l'idée originale de cette fonction).
- La fonction
-
Complétez la définition récursive de la fonction
est_ABR()qui prend en paramètres un arbre de typeArbreBinet qui renvoieTruesi cet arbre binaire est « de recherche »,Falsesinon.1 2 3 4 5 6
def est_ABR(arbre): """ arbre - ArbreBin, arbre binaire dont les noeuds sont comparables Sortie: bool - True si arbre est un arbre binaire de recherche, False sinon """Exemples
Arbre n°1 :
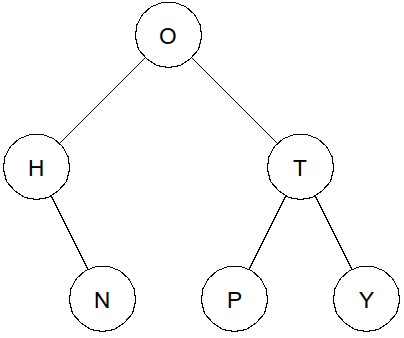
>>> est_ABR(arbre1) TrueArbre n°2 :
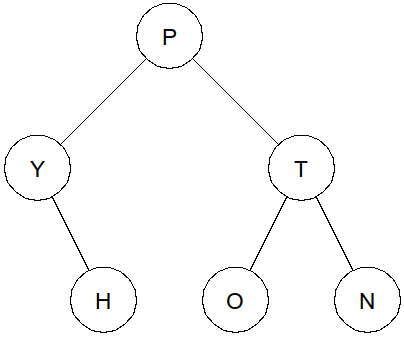
>>> est_ABR(arbre2) FalseUne piste
Il peut être utile de définir une autre fonction qui renvoie
Truesi l'arbre passé en paramètre est réduit à une feuille.Une solution
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
def estFeuille(arbre): """ arbre - ArbreBin, arbre binaire Sortie: bool, True si l'arbre est réduit à une feuille, False sinon """ if est_vide(arbre): return False else: return est_vide(fils_gauche(arbre)) and est_vide(fils_droit(arbre)) def est_ABR(arbre): """ arbre - ArbreBin, arbre binaire dont les noeuds sont comparables Sortie: bool - True si arbre est un arbre binaire de recherche, False sinon """ if est_vide(arbre) or estFeuille(arbre): return True else: x = racine(arbre) if est_vide(fils_gauche(arbre)): return (racine(fils_droit(arbre)) > x) and est_ABR(fils_droit(arbre)) elif est_vide(fils_droit(arbre)): return (racine(fils_gauche(arbre)) <= x) and est_ABR(fils_gauche(arbre)) else: return (racine(fils_gauche(arbre)) <= x < racine(fils_droit(arbre))) and est_ABR(fils_gauche(arbre)) and est_ABR(fils_droit(arbre))
ProgE02.62 - Arbre binaire de recherche équilibré☘
-
Téléchargez le module TAD_ArbresBin.py qui contient une implémentation d'arbre binaire et placez ce module dans votre répertoire de travail.
L'interface est celle donnée dans le cours.Rappels
Méthode/Opérations Description A = ArbreBin(rac, fg, fd)Initialisation d'un arbre binaire de racine rac, de fils gauche et fils droit les arbresfgetfd. Ces trois paramètres sont initialisés àNonepar défautest_vide(A)Renvoie Truesi l'arbre est vide,Falsesinon.racine(A)Renvoie la valeur de la racine de l’arbre Asi cette racine existe,Nonesinon.fils_gauche(A)Renvoie le sous-arbre (fils) gauche de Asi ce sous-arbre existe, un arbre vide sinon.fils_droit(A)Renvoie le sous-arbre (fils) gauche de Asi ce sous-arbre existe, un arbre vide sinon.Attention
Cette interface n'est pas orientée objet, elle s'utilise de la même manière que dans les exemples du cours et dans le TD.
Affichage
Pour visualiser cet arbre, vous avez deux possibilités :
- La fonction
print()réalise un affichage en ligne de l'arbre A passé en argument. - La fonction
affiche_arbreBin()réalise un affichage en deux dimensions de l'arbre A passé en argument. Cet affichage est effectué à l'aide du moduleturtle(merci à Q. CHAMUSSY, enseignant dans l'académie de Lyon, pour l'idée originale de cette fonction).
- La fonction
-
Complétez la définition récursive de la fonction
creer_ABR_equilibre()qui prend en paramètres un tableau non vide d'éléments comparables et triés par ordre croissant. Cette fonction renvoie un arbre de typeArbreBindans lequel les éléments du tableau ont été insérés au mieux pour obtenir un arbre binaire de recherche équilibré.1 2 3 4 5 6
def creer_ABR_equilibre(tab): """ tab - list, tableau NON VIDE d'éléments comparables, triés par ordre croissant Sortie: ArbreBin - Arbre binaire dans lequel les éléments de tab sont insérés au mieux pour obtenir un arbre binaire de recherche équilibré """Exemple
>>> arbre3 = creer_ABR_equilibre(list(range(18))) >>> affiche_arbreBin(arbre3)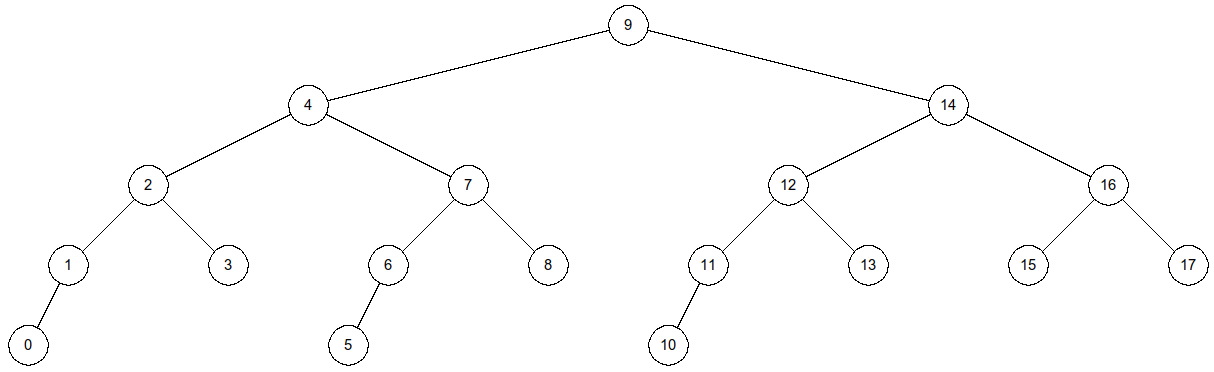
Une piste
Il peut être utile de définir une autre fonction qui permet de « trancher » un tableau selon deux indices donnés en paramètres.
Une autre piste
Divisez pour régner.
Une solution
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
def trancher(tab, i, j): """ tab - list, tableau d'éléments i, j - int, entiers tels que 0 <= i <= j < len(tab) Sortie: list, tableau tab[i..j], c'est-à-dire [tab(i], tab[i+1], .., tab[j]] >>> trancher([2, 6, 3, 9, 4, 42], 1, 4) [6, 3, 9, 4] """ result = [] for k in range(i, j+1): result.append(tab[k]) return result def creer_ABR_equilibre(tab): """ tab - list, tableau NON VIDE d'éléments comparables, triés par ordre croissant Sortie: ArbreBin - Arbre binaire dans lequel les éléments de tab sont insérés au mieux pour obtenir un arbre binaire de recherche équilibré """ if len(tab) == 0: return None elif len(tab) == 1: return ArbreBin(tab[0]) else: m = len(tab)//2 tab1 = trancher(tab, 0, m-1) tab2 = trancher(tab, m+1, len(tab)-1) return ArbreBin(tab[m], creer_ABR_equilibre(tab1), creer_ABR_equilibre(tab2))
ProgE02.63 - Annuaire☘
On souhaite stocker un annuaire téléphonique sous la forme d'un arbre binaire de recherche.
Chaque entrée de l'annuaire est un noeud de l'arbre et contient deux
informations : un nom (self.nom) et un numéro de téléphone (self.numero).
De plus, chaque noeud a un fils gauche (self.filsG) et un fils droit
(self.filsD) qui ne sont jamais None.
Les attributs self.nom et self.numero d'un annuaire vide sont égaux à None.
Les éléments de l'arbre sont triés en fonction des noms des contacts.
L'ordre utilisé est l'ordre lexicographique (c'est-à-dire l'ordre alphabétique
étendu aux autres caractères que les lettres).
Remarque
C'est l'ordre par défaut de Python pour les chaînes de caractères.
Par exemple :
>>> `"au revoir" < "bonjour"`
True
-
Téléchargez le fichier arbre_annuaire.py.
Si vous exécutez le fichier maintenant, un annuaire contenant un seul numéro s'affiche, et la console indique :
Numéro de Mélanie incorrect Numéro de Dylan incorrect -
Dans ce fichier, plusieurs fonctions sont déjà définies. En particulier, la fonction
est_vide()peut vous être utile.
Complétez la définition de la fonction récursiveajouter_contact()en respectant ses spécifications (notez que le cas où l'annuaire est vide est déjà codé) :1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
def ajouter_contact(self, nom, numero): """ Ajoute un nouveau contact à l'arbre. Renvoie None. """ assert nom is not None and numero is not None, "Le nom et le numéro du contact à ajouter ne peuvent pas être None" if self.est_vide(): # Si l'annuaire est vide self.nom = nom self.numero = numero self.filsG = ArbreAnnuaire() self.filsD = ArbreAnnuaire() else: # Si l'annuaire n'est pas vide # TODO passExemple
Si le code est correct, l'arbre suivant devrait s'afficher en exécutant le fichier :
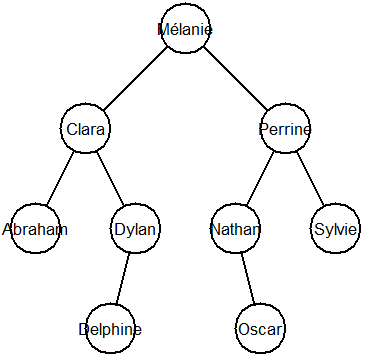
Une réponse
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
def ajouter_contact(self, nom, numero): """ Ajoute un nouveau contact à l'arbre. Renvoie None. """ assert nom is not None and numero is not None, "Le nom et le numéro du contact à ajouter ne peuvent pas être None" if self.est_vide(): # Si l'annuaire est vide self.nom = nom self.numero = numero self.filsG = ArbreAnnuaire() self.filsD = ArbreAnnuaire() else: # Si l'annuaire n'est pas vide if nom < self.nom: self.filsG.ajouter_contact(nom, numero) else: self.filsD.ajouter_contact(nom, numero) -
Complétez la définition de la fonction récursive
numero_contact():1 2 3 4 5
def numero_contact(self, nom): """ Renvoie le numéro d'un contact s'il est dans l'arbre, None sinon. """ passExemple
Si le code est correct, la console devrait maintenant indiquer en exécutant le fichier :
Numéro de Mélanie correct Numéro de Dylan correctUne réponse
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
def numero_contact(self, nom): """ Renvoie le numéro d'un contact s'il est dans l'arbre, None sinon. """ if self.est_vide(): # Si l'annuaire est vide return None else: # Si l'annuaire n'est pas vide if nom == self.nom: return self.numero elif nom < self.nom: return self.filsG.numero_contact(nom) else: return self.filsD.numero_contact(nom)
ProgE02.64 - Nouvelle implémentation d'ABR☘
On souhaite implémenter une structure d'arbre binaire de recherche sous la forme
d'une classe ArbreBinRecherche possédant un seul attribut arbre de type
list (un tableau). Cet attribut comporte au moins deux éléments.
- Le premier élément du tableau
arbrecontient la taille (c'est-à-dire le nombre de noeuds) de l'arbre. - La valeur de la racine est située à l'indice 1.
- La racine du sous-arbre gauche du nœud d'indice
ia pour indice2*i. - La racine du sous-arbre droit du nœud d'indice
ia pour indice2*i+1.
Exemples
-
La structure d'arbre vide correspond à un attribut
arbrede valeur :[0, None] -
Un arbre réduit à une feuille de valeur
7correspond à un attributarbrede valeur :[1, 7, None, None] 3. L'arbre dessiné ci-contre correspond à un attribut
3. L'arbre dessiné ci-contre correspond à un attribut arbrede valeur :[6, 'O', 'H', 'T', None, 'N', 'P', 'Y', None, None, None, None, None, None, None, None]
- Téléchargez le fichier ProgE02.64.py à compléter.
-
Complétez le constructeur de la classe
ArbreBinRechercheen respectant ses spécifications.Une réponse
1 2 3 4 5 6 7 8 9 10 11 12
def __init__(self, racine=None): """ Initialisation d'un arbre binaire (de recherche) sous la forme d'un tableau dont le premier élément est le nombre de noeuds de l'arbre. La valeur de la racine est située à l'indice 1 Le fils gauche d'un noeud d'indice i est situé à l'indice 2*i Le fils droit d'un noeud d'indice i est situé à l'indice 2*i+1 """ self.arbre = [1, racine] if racine is None: self.arbre[0] = 0 -
Complétez les méthodes
taille()etracine()en utilisant la structure de l'attributarbre.Une réponse
1 2 3 4 5 6 7 8 9 10 11
def taille(self): """ Sortie: int - Nombre de noeuds de l'arbre """ return self.arbre[0] def racine(self): """ Sortie: elt - valeur de la racine, éventuellement None """ return self.arbre[1] -
Complétez les méthodes
est_vide(),est_feuille()et__repr__()en utilisant la structure de l'attributarbre.Exemples
>>> arbre = ArbreBinRecherche() >>> arbre [0, None] >>> arbre.est_vide() True >>> arbre.est_feuille() FalseUne réponse
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
def est_vide(self): """ Sortie: bool - lien True si l'arbre binaire (de recherche) est vide, False sinon """ return self.arbre[0] == 0 def est_feuille(self): """ Sortie: bool - True si l'arbre binaire (de recherche) est réduit à une feuille, False sinon """ return self.arbre[0] == 1 def __repr__(self): """ Sortie: str - Chaîne d'affichage de l'arbre binaire de recherche "en colonne" """ return f"{self.arbre}" -
Complétez la méthode
inserer()qui prend pour paramètre une valeur et l'insère à sa bonne place dans la structure d'arbre binaire de recherche.
On distinguera deux cas :a. ou bien l'emplacement (le niveau) existe déjà et on remplace
Nonepar la valeur dans l'attributarbre;
b. ou bien il faut placer cette valeur dans une feuille d'un niveau qui n'existe pas, alors on agrandit le tableauarbred'un niveau supplémentaire (où toutes les valeurs sont àNone) et on se retrouve dans le cas précédent.Exemples
>>> arbre = ArbreBinRecherche() >>> arbre.inserer(8) >>> arbre [1, 8] >>> arbre.inserer(3) >>> arbre.inserer(1) >>> arbre.inserer(6) >>> arbre [4, 8, 3, None, 1, 6, None, None] >>> arbre.inserer(4) >>> arbre.inserer(7) >>> arbre.inserer(5) >>> arbre.inserer(10) >>> arbre.inserer(14) >>> arbre.inserer(13) >>> arbre [10, 8, 3, 10, 1, 6, None, 14, None, None, 4, 7, None, None, 13, None, None, None, None, None, None, 5, None, None, None, None, None, None, None, None, None, None]Une réponse
Ne pas oublier d'augmenter la taille (le nombre de nœuds) de l'arbre.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
def inserer(self, valeur): """ Sortie: None - insère une valeur dans l'arbre """ indice = 1 while indice < len(self.arbre): if self.arbre[indice] == None: self.arbre[indice] = valeur self.arbre[0] += 1 indice = len(self.arbre) else: if self.arbre[indice] < valeur: indice = 2*indice+1 else: indice = 2*indice if indice >= len(self.arbre): self.arbre += [None]*len(self.arbre) -
Automatisez la méthode précédente en complétant la définition de la méthode
inserer_tab()qui prend pour paramètre un tableau de valeurs et insère successivement chacune des valeurs à sa bonne place dans la structure d'arbre binaire de recherche.Exemples
>>> arbre2 = ArbreBinRecherche() >>> arbre2.inserer_tab([8, 5, 3, 11, 9, 6, 10]) >>> arbre2 [7, 8, 5, 11, 3, 6, 9, None, None, None, None, None, None, 10, None, None]Une réponse
1 2 3 4 5 6
def inserer_tab(self, tab): """ Sortie: None - insère les éléments de tab dans l'arbre """ for elt in tab: self.inserer(elt) -
Complétez la définition de la méthode
hauteur()qui renvoie la hauteur de l'arbre binaire de recherche sur lequel cette méthode est appliquée.Exemples
>>> arbre2.hauteur() 4Une réponse
1 2 3 4 5 6 7 8 9 10 11
def hauteur(self): """ Sortie: int - Hauteur de l'arbre (1 pour un arbre réduit à une feuille) """ h = -1 t = len(self.arbre) while t > 0: h = h+1 t = t//2 return h -
Complétez les définitions des méthodes
minimum()etmaximum()qui renvoient respectivement la plus petite et la plus grande valeur contenue dans l'arbre.Exemples
>>> arbre2.minimum() 3 >>> arbre2.maximum() 11Une réponse
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
def minimum(self): """ Sortie: plus petite valeur d'un noeud de l'arbre """ indice = 1 while 2*indice < len(self.arbre) and self.arbre[2*indice] is not None: indice = 2*indice return self.arbre[indice] def maximum(self): """ Sortie: plus grande valeur d'un noeud de l'arbre """ indice = 1 while 2*indice+1 < len(self.arbre) and self.arbre[2*indice+1] is not None: indice = 2*indice+1 return self.arbre[indice] -
Complétez la définition de la méthode
rechercher()qui prend en paramètre une valeur de même type que les éléments contenus dans l'arbre et qui renvoieTruesi cette valeur est dans l'arbre,Falsesinon.Exemples
>>> arbre2.rechercher(9) True >>> arbre2.rechercher(13) FalseUne réponse
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
def rechercher(self, valeur): """ valeur: élément de même nature que les noeuds de l'arbre Sortie: bool – True si la valeur val est dans l’arbre, False sinon. """ i = 1 while i <= len(self.arbre): if self.arbre[i] is None: return False elif self.arbre[i] == valeur: return True elif self.arbre[i] > valeur: i = 2*i elif self.arbre[i] < valeur: i = 2*i+1 return FalseUne réponse en « trichant »
1 2 3 4 5 6 7
def rechercher(self, valeur): """ valeur: élément de même nature que les noeuds de l'arbre Sortie: bool – True si la valeur val est dans l’arbre, False sinon. """ return valeur in self.arbre -
Complétez les définitions des méthodes
fils_gauche()etfils_droit()qui renvoient un nouvel arbre binaire de recherche, respectivement le sous-arbre gauche et le sous-arbre droit.Exemples
On rappelle que le premier élément du tableau correspond au nombre de noeuds de l'arbre.
>>> arbre2.fils_gauche() [3, 5, 3, 6] >>> arbre2.fils_droit() [3, 11, 9, None, None, 10, None, None]Une réponse
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
def fils_gauche(self): """ Sortie: ArbreBinR - Fils gauche de l'arbre """ fg = ArbreBinRecherche() file_indices = [2] while file_indices != []: indice_noeud = file_indices.pop(0) if self.arbre[indice_noeud] is not None: fg.inserer(self.arbre[indice_noeud]) if 2*indice_noeud < len(self.arbre): file_indices.append(2*indice_noeud) file_indices.append(2*indice_noeud+1) return fg def fils_droit(self): """ Sortie: ArbreBinR - Fils droit de l'arbre """ fd = ArbreBinRecherche() file_indices = [3] while file_indices != []: indice_noeud = file_indices.pop(0) if self.arbre[indice_noeud] is not None: fd.inserer(self.arbre[indice_noeud]) if 2*indice_noeud < len(self.arbre): file_indices.append(2*indice_noeud) file_indices.append(2*indice_noeud+1) return fd -
Pour mieux visualiser l'arbre dans la console, complétez la définition de la méthode récursive
affiche()en appliquant le parcours en profondeur qui convient.Exemples
>>> arbre.affiche() 1 3 4 5 6 7 8 10 13 14 >>> arbre2.affiche() 3 5 6 8 9 10 11
ProgE02.65 - Annuaire (la suite, en plus délicat)☘
L'objectif de cet exercice est de coder l'algorithme de suppression d'un élément dans un arbre binaire de recherche.
-
Avant tout, reprenez le code complété de l'exercice sur l'annuaire téléphonique (ProgE02.63).
-
Complétez ce code en copiant/collant/ajoutant les méthodes suivantes à la classe
ArbreAnnuaire). Faîtes l'effort de comprendre leur rôle, elles vous aideront pour la réalisation de la fonction de suppression.18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48
def copier(self, autre_arbre): """ Transforme l'arbre en une copie d'un autre arbre. """ self.nom = autre_arbre.nom self.numero = autre_arbre.numero self.filsG = autre_arbre.filsG self.filsD = autre_arbre.filsD def noeud_max(self): """ Renvoie le sous-arbre ayant pour racine le maximum de l'arbre. """ assert not self.est_vide() if not self.filsD.est_vide(): return self.filsD.noeud_max() else: return self def noeud_min(self): """ Renvoie le sous-arbre ayant pour racine le minimum de l'arbre. """ assert not self.est_vide() if not self.filsG.est_vide(): return self.filsG.noeud_min() else: return self -
Dans la classe
ArbreAnnuaire, copiez/collez la méthode « à trous » suivante :109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127
def supprimer_contact(self, nom): """ Supprime le contact ayant le nom passé en argument. Renvoie None. """ assert not self.est_vide(), "Nom inexistant dans l'annuaire" if nom == self.nom: # TODO 3 pass elif nom < self.nom: # TODO 1 pass else: # TODO 2 passDe plus, à la fin de la fonction
test(), avant la ligneannuaire.affichage(), ajoutez les lignes suivantes :226 227 228
annuaire.supprimer_contact("Nathan") annuaire.supprimer_contact("Delphine") annuaire.supprimer_contact("Mélanie") -
Complétez les cas
TODO 1etTODO 2, c'est-à-dire quand le contact à supprimer n'est pas le noeud courant.Une solution
109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125
def supprimer_contact(self, nom): """ Supprime le contact ayant le nom passé en argument. Renvoie None. """ assert not self.est_vide(), "Nom inexistant dans l'annuaire" if nom == self.nom: # TODO 3 pass elif nom < self.nom: self.filsG.supprimer_contact(nom) else: self.filsD.supprimer_contact(nom) -
On s'intéresse au cas
TODO 3.
Rappelez quels sont les trois sous-cas à considérer lors de la suppression d'un élément dans un arbre binaire de recherche. N'hésitez pas à reprendre vos exercices de TD.Une solution
Ou bien le nœud est une feuille, alors on le supprime.
Ou bien le nœud ne possède qu'un seul fils, alors on le remplace par la racine de ce fils. Ou bien le nœud possède deux enfants, alors on le remplace par le plus grand des nœuds inférieurs (ou le plus petit des nœuds supérieurs) puis on supprime ce nœud. -
Si l'annuaire représenté par le fils gauche est vide, comment peut-on supprimer le noeud courant ?
Coder ce cas.Après exécution de l'appel
test()En exécutant le fichier, vous devriez obtenir l'affichage d'arbre suivant :
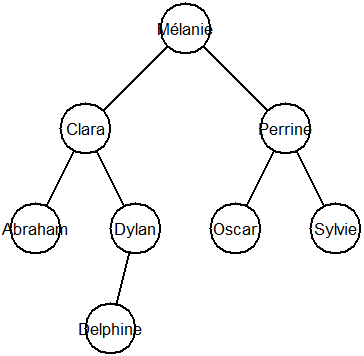
Une solution
On remplace le nœud courant par son fils droit :
109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127
def supprimer_contact(self, nom): """ Supprime le contact ayant le nom passé en argument. Renvoie None. """ assert not self.est_vide(), "Nom inexistant dans l'annuaire" if nom == self.nom: if self.filsG.est_vide(): self.copier(self.filsD) pass elif nom < self.nom: self.filsG.supprimer_contact(nom) else: self.filsD.supprimer_contact(nom) -
Si l'annuaire représenté par le fils droit est vide, comment peut-on supprimer le noeud courant ?
Coder ce cas.Après exécution de l'appel
test()En exécutant le fichier, vous devriez obtenir l'affichage d'arbre suivant :
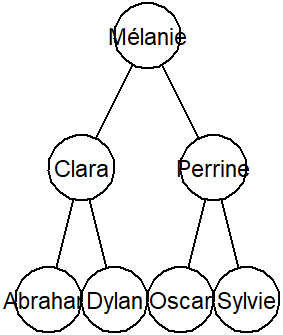
Une solution
On remplace le nœud courant par son fils gauche :
109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129
def supprimer_contact(self, nom): """ Supprime le contact ayant le nom passé en argument. Renvoie None. """ assert not self.est_vide(), "Nom inexistant dans l'annuaire" if nom == self.nom: if self.filsG.est_vide(): self.copier(self.filsD) elif self.filsD.est_vide(): self.copier(self.filsG) pass elif nom < self.nom: self.filsG.supprimer_contact(nom) else: self.filsD.supprimer_contact(nom) -
Sinon, aucun des fils n'est un annuaire vide. Comment peut-on supprimer le noeud courant ?
Coder ce cas.Après exécution de l'appel
test()En exécutant le fichier, vous devriez obtenir l'affichage d'arbre suivant :
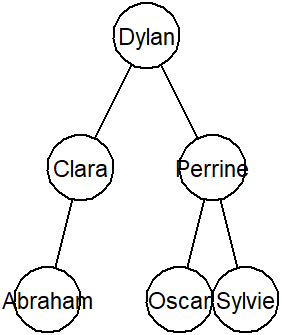
Une solution
On remplace le nœud courant par le plus grand des nœuds inférieurs :
109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137
def supprimer_contact(self, nom): """ Supprime le contact ayant le nom passé en argument. Renvoie None. """ assert not self.est_vide(), "Nom inexistant dans l'annuaire" if nom == self.nom: if self.filsG.est_vide(): self.copier(self.filsD) elif self.filsD.est_vide(): self.copier(self.filsG) else: noeud_echange = self.filsG.noeud_max() self.nom = noeud_echange.nom self.numero = noeud_echange.numero noeud_echange.copier(noeud_echange.filsG) # Alternativement : # noeud_echange = self.filsD.noeud_min() # self.nom = noeud_echange.nom # self.numero = noeud_echange.numero # noeud_echange.copier(noeud_echange.filsD) elif nom < self.nom: self.filsG.supprimer_contact(nom) else: self.filsD.supprimer_contact(nom)