Aller au contenu

TP - Représentations informatiques☘

Il existe plusieurs méthodes pour implémenter un graphe en machine (matrice d'adjacence ou de pondération, liste des voisins, des successeurs ou des prédécesseurs).

Dans ce TP, vous allez définir des fonctions permettant de passer d'une représentation à l'autre. Vous définirez aussi une fonction d'affichage dont le résultat est inteprétable par le logiciel GraphViz.

Téléchargez le fichier « à trous » TPA05.10.py (clic droit -> [Enregistrer la cible du lien sous]) et enregistrez-le dans le dossier [A05-Graphes].

Partie A - Graphes non pondérés☘

Dans cette partie, vous allez programmer les fonctions permettant de passer d'une matrice d'adjacence au dictionnaire de listes des voisins (ou des successeurs) correspondant et vice-versa.

Contraintes

  • Les matrices sont carrées et leurs éléments valent soit 0, soit 1.
  • Les clefs des dictionnaires sont des entiers partant de 0 et incrémentés de 1 en 1.
    Les valeurs associées sont des tableaux d'entiers, pas forcément de taille identique.

  1. Complétez la définition de la fonction matrice_adj_to_liste() en respectant ses spécifications. 

    1
2
3
4
5
6
7
    def matrice_adj_to_liste(matrice):
    """
    matrice - list, tableau 2D représentant une matrice d'adjacence associée à un graphe (orienté ou non)
    Sortie: dict - dictionnaire tel que:
                   les clefs sont les numéros associés aux sommets du graphe
                   les valeurs sont un tableau des voisins (ou successeurs) du sommet
    """

    Exemples de test

    Vous pouvez effectuer les tests suivants, puis ajouter vos propres tests basés sur les exercices effectués en TD. 

    >>> M1 = [[0, 1, 1, 0, 0], [1, 0, 0, 0, 1], [1, 0, 0, 1, 1], [0, 0, 1, 0, 1], [0, 1, 1, 1, 0]]
>>> matrice_adj_to_liste(M1)
{0: [1, 2],
 1: [0, 4],
 2: [0, 3, 4],
 3: [2, 4],
 4: [1, 2, 3]}

>>> M2 = [[0, 1, 1, 0, 0], [0, 0, 1, 0, 1], [1, 0, 0, 0, 1], [1, 0, 1, 0, 1], [0, 1, 1, 1, 0]]
>>> matrice_adj_to_liste(M2)
{0: [1, 2],
 1: [2, 4],
 2: [0, 4],
 3: [0, 2, 4],
 4: [1, 2, 3]}

  2. Complétez la définition de la fonction liste_to_matrice_adj() en respectant ses spécifications. 

    1
2
3
4
5
6
7
    def liste_to_matrice_adj(dico):
    """
    dico - dictionnaire tel que:
                les clefs sont les numéros associés aux sommets d'un graphe (orienté ou non)
                les valeurs sont un tableau des voisins (ou successeurs) du sommet
    Sortie: list - tableau 2D représentant la matrice d'adjacence associée au graphe
    """

    Exemples de test

    Vous pouvez effectuer les tests suivants, puis ajouter vos propres tests basés sur les exercices effectués en TD. 

    >>> L1 = {0: [1, 2], 1: [0, 4], 2: [0, 3, 4], 3: [2, 4], 4: [1, 2, 3]}
>>> liste_to_matrice_adj(L1)
[[0, 1, 1, 0, 0],
 [1, 0, 0, 0, 1],
 [1, 0, 0, 1, 1],
 [0, 0, 1, 0, 1],
 [0, 1, 1, 1, 0]]

>>> L2 = {0: [1, 2], 1: [2, 4], 2: [0, 4], 3: [0, 2, 4], 4: [1, 2, 3]}
>>> liste_to_matrice_adj(L2)
[[0, 1, 1, 0, 0],
 [0, 0, 1, 0, 1],
 [1, 0, 0, 0, 1],
 [1, 0, 1, 0, 1],
 [0, 1, 1, 1, 0]]

Partie B - Graphes pondérés☘

On s'intéresse à présent à des matrices de pondération contenant des valeurs quelconques.

Contraintes

  • Les matrices sont carrées et leurs éléments sont des nombres (des entiers principalement, mais des flottants sont possibles).
  • Les clefs i des dictionnaires sont des entiers partant de 0 et incrémentés de 1 en 1.
    Les valeurs associées sont des dictionnaires qui, à une clef j, font correspondre la pondération placée en case (i ; j) de la matrice.

  1. Complétez la définition de la fonction matrice_pond_to_dico() en respectant ses spécifications. 

    1
2
3
4
5
6
7
    def matrice_pond_to_dico(matrice):
    """
    matrice - list, tableau 2D représentant une matrice de pondération associée à un graphe pondéré
    Sortie: dict - dictionnaire tel que:
                   les clefs sont les numéros associés aux sommets du graphe
                   les valeurs sont un dictionnaire {voisins: pondération} du sommet
    """

    Exemples de test

    Vous pouvez effectuer les tests suivants, puis ajouter vos propres tests basés sur les exercices effectués en TD. 

    >>> M3 = [[0, 0, 3, 1, 0], [0, 0, 4, 2, 1], [3, 4, 0, 6, 0], [1, 2, 6, 0, 5], [0, 1, 0, 5, 0]]
>>> matrice_pond_to_dico(M3)
{0: {2: 3, 3: 1},
 1: {2: 4, 3: 2, 4: 1},
 2: {0: 3, 1: 4, 3: 6},
 3: {0: 1, 1: 2, 2: 6, 4: 5},
 4: {1: 1, 3: 5}}

  2. Complétez la définition de la fonction dico_to_matrice_pond() en respectant ses spécifications. 

    1
2
3
4
5
6
7
    def dico_to_matrice_pond(dico):
    """
    dico - dictionnaire tel que:
                les clefs sont les numéros associés aux sommets d'un graphe pondéré non orienté
                les valeurs sont un dictionnaire {voisins: pondération } du sommet
    Sortie: list - tableau 2D représentant une matrice de pondération associée au graphe
    """

    Exemples de test

    Vous pouvez effectuer les tests suivants, puis ajouter vos propres tests basés sur les exercices effectués en TD. 

    >>> L3 = {0: {2: 3, 3: 1}, 1: {2: 4, 3: 2, 4: 1}, 2: {0: 3, 1: 4, 3: 6}, 3: {0: 1, 1: 2, 2: 6, 4: 5}, 4: {1: 1, 3: 5}}
>>> dico_to_matrice_pond(L3)
[[0, 0, 3, 1, 0],
 [0, 0, 4, 2, 1],
 [3, 4, 0, 6, 0],
 [1, 2, 6, 0, 5],
 [0, 1, 0, 5, 0]]

Partie C - Propriétés d'une matrice☘

  1. Complétez la définition de la fonction est_symetrique() en respectant ses spécifications.
    Attention, programmez un test d'assertion qui vérifie que la matrice passée en argument est bien carrée.

    1
2
3
4
5
    def est_symetrique(matrice):
    """
    matrice - list, tableau 2D d'entiers représentant une matrice carrée
    Sortie: bool - True si la matrice est symétrique, False sinon
    """
    Exemples de test

    Vous pouvez effectuer les tests suivants, puis ajouter vos propres tests basés sur les exercices effectués en TD. 

    >>> M1 = [[0, 1, 1, 0, 0], [1, 0, 0, 0, 1], [1, 0, 0, 1, 1], [0, 0, 1, 0, 1], [0, 1, 1, 1, 0]]
>>> est_symetrique(M1)
True

>>> M2 = [[0, 1, 1, 0, 0], [0, 0, 1, 0, 1], [1, 0, 0, 0, 1], [1, 0, 1, 0, 1], [0, 1, 1, 1, 0]]
>>> est_symetrique(M2)
False

  2. Complétez la définition de la fonction est_pondere() en respectant ses spécifications.
    Attention, programmez un test d'assertion qui vérifie que la matrice passée en argument est bien carrée.

    1
2
3
4
5
6
    def est_pondere(matrice):
    """
    matrice - list, tableau 2D d'entiers représentant une matrice carrée
    Sortie: bool - True si la matrice comporte des valeurs autre que 0 ou 1,
                   False sinon
    """
    Exemples de test

    Vous pouvez effectuer les tests suivants, puis ajouter vos propres tests basés sur les exercices effectués en TD. 

    >>> M1 = [[0, 1, 1, 0, 0], [1, 0, 0, 0, 1], [1, 0, 0, 1, 1], [0, 0, 1, 0, 1], [0, 1, 1, 1, 0]]
>>> est_pondere(M1)
False

>>> M3 = [[0, 0, 3, 1, 0], [0, 0, 4, 2, 1], [3, 4, 0, 6, 0], [1, 2, 6, 0, 5], [0, 1, 0, 5, 0]]
>>> est_pondere(M3)
True

Partie D - Affichage☘

GraphViz est un logiciel open-source qui permet de générer des représentations de graphe sous forme d'images au format .png, .svg, etc...

Remarque importante

Ce logiciel est installable sous n'importe quel système d'exploitation.
Une fois le logciel installé, il est même possible d'installer un module complémentaire Python 

pip install graphviz
afin d'y avoir accès directement dans votre programme.

Cette installation est parfois délicate sous système d'exploitation Windows c'est pourquoi nous utiliserons à la place une application web pour obtenir l'image du graphe correspondant à une matrice carrée (d'adjacence ou de pondération).

  1. Un premier test de l'interface.

    1. Ouvrez la page https://dreampuf.github.io/GraphvizOnline/. Vous pouvez voir un premier tracé (élaboré) de graphe.
    2. Vous allez programmer l'affichage de ce premier graphe non orienté : Graphe non orienté 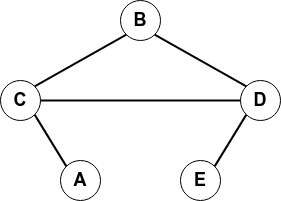Pour cela, copiez/collez et essayez d'analyser les instructions suivantes : 
      1
2
3
4
5
6
      graph G1 {
    A -- C ;
    C -- B ;
    C -- D ;
    B -- D ;
    D -- E }
    3. Vous pouvez changer le format de l'image (svg, png, etc...).
      En effectuant un clic gauche sur l'image, vous pouvez alors la télécharger dans votre répertoire de travail.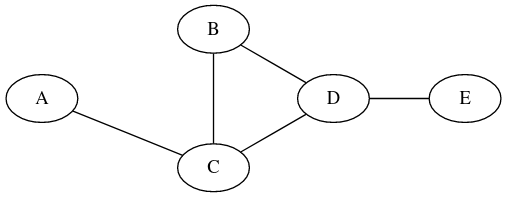 Graphe non orienté

    4. Puis programmez l'affichage de ce second graphe orienté : 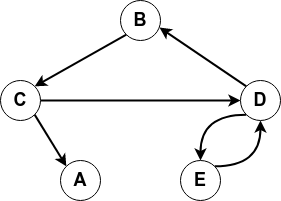Graphe non orienté Pour cela, copiez/collez et complétez les instructions suivantes : 

      1
2
3
4
      digraph G2 {
    C -> A ;
    B -> C ;
    ... }

      Une réponse

      1
2
3
4
5
6
7
      digraph G2 {
    C -> A ;
    B -> C ;
    D -> B ;
    C -> D ;
    D -> E ;
    E -> D }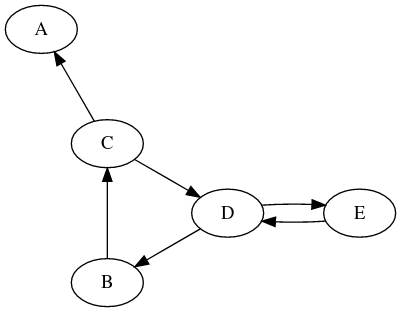
      Graphe non orienté

  2. Le logiciel Graphviz comporte une multitude d'instructions que nous n'allons pas aborder dans le cadre de ce TP.

    Instructions à retenir

    Graphe non orienté

    • La définition d'un graphe non orienté nommé G commence par : 
      graph G {
      où G est le nom du graphe.
    • Chaque arête est symbolisée par le double tiret « -- » entre deux noms de sommet, puis on termine par un point-virgule : 
      A -- B ;
    • Si l'arête est pondérée, on fait suivre sa définition du label correspondant : 
      A -- B [label = 5] ;
    • On termine la définition du grapheà l'aide d'une accolade fermante : 
      }

    Graphe orienté

    • La définition d'un graphe orienté G commence par : 
      digraph G {
    • Chaque arc est symbolisée par un tiret suivi du symbole supérieur « -> » entre deux noms de sommet, puis on termine par un point-virgule : 
      A -> B ;
    • Si l'arc est pondéré, on fait suivre sa définition du label correspondant : 
      A -> B [label = 5] ;
    • On termine la définition du graphe à l'aide d'une accolade fermante : 
      }

    Complétez la définition de la fonction affiche_graphviz() en respectant ses spécifications.

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
    def affiche_graphviz(matrice, oriente = False, pondere = False, tab_sommets=None):
    """
    matrice - list, tableau 2D d'entiers représentant une matrice carrée associée à un graphe
    oriente - bool, True si le graphe est orienté, False par défaut
    pondere - bool, True si le graphe est pondéré, False par défaut
    tab_sommets - list, tableau comportant les étiquettes associées au noeud du graphe.
                        A l'indice i, on trouve l'étiquette du sommet i
    Sortie: None - Affichage sous un format interprétable par GraphViz
                   https://dreampuf.github.io/GraphvizOnline/
    """
    Une piste

    Commencez par programmer un affichage pour un graphe non orienté, non pondéré, c'est-à-dire sans tenir compte des paramètres oriente, pondere et tab_sommets.
    Attention qu'il n'y ait pas de doublon d'arêtes !

    Dans un second temps, prenez en compte un premier paramètre parmi ces trois là, puis un deuxième, et enfin le troisième.

    Test de graphe non orienté, non pondéré, sans étiquettes
    >>> M1 = [[0, 1, 1, 0, 0], [1, 0, 0, 0, 1], [1, 0, 0, 1, 1], [0, 0, 1, 0, 1], [0, 1, 1, 1, 0]]
>>> affiche_graphviz(M1)
graph G {
0 -- 1 ;
0 -- 2 ;
1 -- 4 ;
2 -- 3 ;
2 -- 4 ;
3 -- 4 ;
}
    Test de graphe orienté, non pondéré, sans étiquettes
    >>> M2 = [[0, 1, 1, 0, 0], [0, 0, 1, 0, 1], [1, 0, 0, 0, 1], [1, 0, 1, 0, 1], [0, 1, 1, 1, 0]]
>>> affiche_graphviz(M2, True)
digraph G {
0 -> 1 ;
0 -> 2 ;
1 -> 2 ;
1 -> 4 ;
2 -> 0 ;
2 -> 4 ;
3 -> 0 ;
3 -> 2 ;
3 -> 4 ;
4 -> 1 ;
4 -> 2 ;
4 -> 3 ;
}
    Test de graphe orienté et pondéré, sans étiquettes
    >>> M3 = [[0, 0, 3, 1, 0], [0, 0, 4, 2, 1], [3, 4, 0, 6, 0], [1, 2, 6, 0, 5], [0, 1, 0, 5, 0]]
>>> affiche_graphviz(M3, True, True)
digraph G {
0 -> 2 [label = 3] ;
0 -> 3 [label = 1] ;
1 -> 2 [label = 4] ;
1 -> 3 [label = 2] ;
1 -> 4 [label = 1] ;
2 -> 0 [label = 3] ;
2 -> 1 [label = 4] ;
2 -> 3 [label = 6] ;
3 -> 0 [label = 1] ;
3 -> 1 [label = 2] ;
3 -> 2 [label = 6] ;
3 -> 4 [label = 5] ;
4 -> 1 [label = 1] ;
4 -> 3 [label = 5] ;
}
    Test de graphe non orienté et non pondéré, avec étiquettes
    >>> M1 = [[0, 1, 1, 0, 0], [1, 0, 0, 0, 1], [1, 0, 0, 1, 1], [0, 0, 1, 0, 1], [0, 1, 1, 1, 0]]
>>> affiche_graphviz(M1, False, False, ['A', 'B', 'C', 'D', 'E'])
graph G {
A -- B ;
A -- C ;
B -- E ;
C -- D ;
C -- E ;
D -- E ;
}

Partie E - Liste des prédécesseurs☘

Dans cette partie, les matrices considérées sont associées à des graphes orientés.

  1. Complétez la définition de la fonction matrice_to_predecesseurs() en respectant ses spécifications. 

    1
2
3
4
5
6
7
    def matrice_to_predecesseurs(matrice):
    """
    matrice - list, tableau 2D représentant une matrice d'adjacence associée à un graphe orienté
    Sortie: dict - dictionnaire tel que:
                   les clefs sont les numéros associés aux sommets du graphe
                   les valeurs sont un tableau des prédécesseurs du sommet
    """

    Exemple de test

    Vous pouvez effectuer les tests suivants, puis ajouter vos propres tests basés sur les exercices effectués en TD. 

    >>> M4 = [[0, 1, 1, 0, 0], [0, 0, 1, 0, 1], [1, 0, 0, 0, 1], [1, 0, 1, 0, 1], [0, 1, 1, 1, 0]]
>>> matrice_to_predecesseurs(M4)
{0: [2, 3],
 1: [0, 4],
 2: [0, 1, 3, 4],
 3: [4],
 4: [1, 2, 3]}

  2. Complétez la définition de la fonction predecesseurs_to_matrice() en respectant ses spécifications. 

    1
2
3
4
5
6
7
    def predecesseurs_to_matrice(dico):
    """
    dico - dictionnaire tel que:
                les clefs sont les numéros associés aux sommets d'un graphe orienté
                les valeurs sont un tableau des prédécesseurs du sommet
    Sortie: list - tableau 2D représentant une matrice d'adjacence associée au graphe
    """

    Exemples de test

    Vous pouvez effectuer les tests suivants, puis ajouter vos propres tests basés sur les exercices effectués en TD. 

    >>> L4 = {0: [2, 3], 1: [0, 4], 2: [0, 1, 3, 4], 3: [4], 4: [1, 2, 3]}
>>> predecesseurs_to_matrice(L4)
[[0, 1, 1, 0, 0],
 [0, 0, 1, 0, 1],
 [1, 0, 0, 0, 1],
 [1, 0, 1, 0, 1],
 [0, 1, 1, 1, 0]]