TP - Implémenter une structure de graphe☘

Ce TP doit conduire à créer de A à Z deux modules utilisables tout le reste de l'année. Enregistrez ces fichiers dans un dossier intitulé [Mes_modules] sous les noms donnés.

Remarque importante

La partie 1 va vous conduire à implémenter, sous la forme d'une classe GrapheOriente, les graphes orientés à partir d'un dictionnaire de listes de sucesseurs.
La partie 2 vous fera implémenter les graphes non orientés à partir d'un dictionnaire de listes de voisins et sous la forme d'une classe Graphe.

Méthodes autorisées

Les méthodes usuelles sur les listes Python sont autorisées, à savoir :

.append() ;
.pop() ;
.remove() ;
.index() ;

Partie 1 - Classe `GrapheOriente`☘

Téléchargez le fichier « à trous » graphes_orientes.py (clic droit -> [Enregistrer la cible du lien sous]) et enregistrez-le dans le dossier [Mes_modules].

Les objets de la classe GrapheOriente sont munis d'un unique attribut : graphe_dico initialisé à None par défaut. Cet attribut est un dictionnaire contenant, pour chaque sommet du graphe, la liste (éventuellement vide) de ses successeurs.

Exemple d'initialisation

Le graphe orienté : 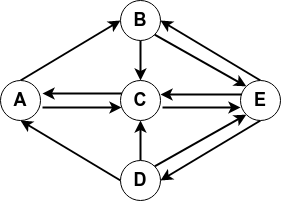sera implémenté de la façon suivante :

L1 = {'A': ['B', 'C'],
     'B': ['C', 'E'],
     'C': ['A', 'E'],
     'D': ['A', 'C', 'E'],
     'E': ['B', 'C', 'D']}
G = GrapheOriente(L1)

Complétez les méthodes de classe suivantes :

.__init__() : initialisation de l'attribut graphe_dico.
.est_vide() : renvoie True si le graphe ne contient aucun sommet.
.sommets() : renvoie un tableau des sommets du graphe.
.arcs() : renvoie un tableau des arcs du graphe. Ces arcs sont définis sous la forme d'un couple (sommet_depart, sommet_arrivee).
.__str__() : renvoie une chaîne de caractères compatible avec le logiciel Graphviz.

Plan de test

On définit un graphe « à la main » :

if __name__ == "__main__":
    L1 = {'A': ['B', 'C'],
         'B': ['C', 'E'],
         'C': ['A', 'E'],
         'D': ['A', 'C', 'E'],
         'E': ['B', 'C', 'D']}
    G = GrapheOriente(L1)

Puis on teste dans la console :

>>> G.est_vide()
False

>>> G.sommets()
['A', 'B', 'C', 'D', 'E']

>>> G.arcs()
[('A', 'B'), ('A', 'C'), ('B', 'C'), ('B', 'E'), ('C', 'A'), ('C', 'E'), ('D', 'A'), ('D', 'C'), ('D', 'E'), ('E', 'B'), ('E', 'C'), ('E', 'D')]

>>> print(G)
digraph G {
A -> B ;
A -> C ;
B -> C ;
B -> E ;
C -> A ;
C -> E ;
D -> A ;
D -> C ;
D -> E ;
E -> B ;
E -> C ;
E -> D ;
}

>>> G2 = GrapheOriente()

>>> G2.est_vide()
True

>>> G2.sommets()
[]

>>> G2.arcs()
[]

>>> print(G2)
digraph G {
}

Complétez les méthodes de classe suivantes :
1. .ordre() : Renvoie l'ordre du graphe.
2. .est_present() : renvoie True la valeur passée en paramètre est un des sommets du graphe, False sinon.
3. .degre() : renvoie le degré du sommet passé en paramètre.
  Si ce sommet n'appartient pas au graphe, une erreur d'assertion doit survenir :
```
>>> G2.degre('A')
AssertionError: le sommet A n'appartient pas au graphe
```
4. .successeurs() : renvoie le tableau des successeurs du sommet passé en paramètre.
  Si ce sommet n'appartient pas au graphe, une erreur d'assertion doit survenir :
```
>>> G2.successeurs('A')
AssertionError: le sommet A n'appartient pas au graphe
```
5. .est_successeur() : renvoie True si le premier sommet passé en paramètre est le successeur du second sommet, False sinon.
  Si le second sommet n'appartient pas au graphe, une erreur d'assertion doit survenir :
```
>>> G.est_successeur('A', 'F')
AssertionError: le sommet F n'appartient pas au graphe
```
6. .predecesseurs() : renvoie le tableau des prédécesseurs du sommet passé en paramètre.
  
  Question
  Un test d'assertion est inutile ici. À votre avis pourquoi ?
7. .est_predecesseur() : renvoie True si le premier sommet passé en paramètre est le prédécesseur du second sommet, False sinon.
  À nouveau, si le premier sommet n'appartient pas au graphe, une erreur d'assertion doit survenir :
```
>>> G.est_predecesseur('F', 'A')
AssertionError: le sommet F n'appartient pas au graphe
```
Plan de test
```
>>> G.ordre()
5

>>> G.degre('A')
2

>>> G.successeurs('A')
['B', 'C']

>>> G.est_successeur('A', 'B')
False

>>> G.est_successeur('B', 'A')
True

>>> G.predecesseurs('A')
['C', 'D']

>>> G.est_predecesseur('A', 'B')
True

>>> G.est_predecesseur('B', 'A')
False
```

Complétez les méthodes de classe suivantes :

.ajoute_sommet() : Ajoute le sommet passé en paramètre dans le graphe à condition que celui-ci ne soit pas déjà présent.
Cette méthode ne renvoie rien.
.supprime_sommet() : Supprime du graphe le sommet passé en paramètre (si celui-ci est présent).
Cette méthode ne renvoie rien.

Une piste
N'oubliez pas qu'un sommet peut être au départ ou bien à l'arrivée d'un arc...
.ajoute_arc() : Cette fonction prend en paramètre un couple de sommet. Si le premier sommet n'est pas présent dans le graphe, il y est ajouté puis l'arc entre les deux sommets est ajouté à condition qu'il ne soit pas déjà présent.
Cette méthode ne renvoie rien.
.supprime_arc() : Supprime l'arc correspondant du graphe. Cette méthode ne renvoie rien.
Si le premier sommet n'appartient pas au graphe, ou si l'arc n'existe pas, des erreurs d'assertion doivent survenir :
```
>>> G.supprime_arc( ('F', 'D') )
AssertionError: le sommet F n'appartient pas au graphe

>>> G.supprime_arc( ('A', 'D') )
AssertionError: l'arc ('A', 'D') n'appartient pas au graphe
```
.matrice() : renvoie la matrice d'adjacence du graphe, ainsi que le tableau des étiquettes des sommets afin de pouvoir établir une correspondance entre étiquette et indice dans la matrice.

Plan de test

>>> G.ajoute_sommet('F')        
>>> G.est_present('F')
True

>>> G.successeurs('F')
[]

>>> G.supprime_sommet('E')        
>>> print(G)
digraph G {
A -> B ;
A -> C ;
B -> C ;
C -> A ;
D -> A ;
D -> C ;
}

>>> G.ajoute_arc( ('F', 'A') )
>>> G.ajoute_arc( ('F', 'C') )
>>> G.ajoute_arc( ('A', 'B') )
>>> G.ajoute_arc( ('G', 'F') )
>>> print(G)
digraph G {
A -> B ;
A -> C ;
B -> C ;
C -> A ;
D -> A ;
D -> C ;
F -> A ;
F -> C ;
G -> F ;
}

>>> G.supprime_arc( ('C', 'A') )
>>> print(G)
digraph G {
A -> B ;
A -> C ;
B -> C ;
D -> A ;
D -> C ;
F -> A ;
F -> C ;
G -> F ;
}

>>> G.matrice()
(['A', 'B', 'C', 'D', 'F', 'G'],
 [[0, 1, 1, 0, 0, 0],
  [0, 0, 1, 0, 0, 0],
  [0, 0, 0, 0, 0, 0],
  [1, 0, 1, 0, 0, 0],
  [1, 0, 1, 0, 0, 0],
  [0, 0, 0, 0, 1, 0]])

Partie 2 - Classe `Graphe`☘

Téléchargez le fichier « à trous » graphes_non_orientes.py (clic droit -> [Enregistrer la cible du lien sous]) et enregistrez-le dans le dossier [Mes_modules].

Les objets de la classe Graphe sont munis d'un unique attribut : graphe_dico initialisé à None par défaut. Cet attribut est un dictionnaire contenant, pour chaque sommet du graphe, la liste (éventuellement vide) de ses voisins.

Exemple d'initialisation

Le graphe : 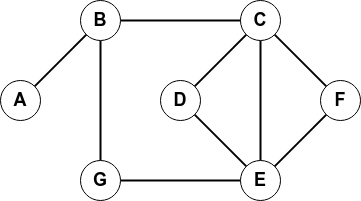Graphe non orienté sera implémenté de la façon suivante :

L2 = {'A': ['B'],
     'B': ['A', 'C', 'G'],
     'C': ['B', 'D', 'E', 'F'],
     'D': ['C', 'E'],
     'E': ['C', 'D', 'F', 'G'],
     'F': ['C', 'E'],
     'G': ['B', 'E']}
G = Graphe(L2)

Important

Dans cette partie, aucun exemple de test n'est proposé. Inspirez-vous des tests de la partie précédente pour élaborez vos propres tests et vérifier votre travail.

Pensez à appeler régulièrement l'enseignant pour vous aider dans cette vérification...

Complétez les méthodes de classe suivantes :

.__init__() : initialisation de l'attribut graphe_dico.
.est_vide() : renvoie True si le graphe ne contient aucun sommet.
.sommets() : renvoie un tableau des sommets du graphe.
.aretes() : renvoie un tableau des arêtes du graphe. Ces arêtes sont définies sous la forme d'un couple (sommet_1, sommet_2).

Attention
Les couples ('A', 'B') et ('B', 'A') correspondent à la même arête. Ils ne peuvent donc pas être présents tous les deux dans le tableau renvoyé par la méthode aretes().
.__str__() : renvoie une chaîne de caractères compatible avec le logiciel Graphviz.
Exemple
Avec l'exemple de graphe proposé au début de cette partie, on obtiendra l'affichage suivant :
```
>>> print(G)
graph G {
A -- B ;
B -- C ;
B -- G ;
C -- D ;
C -- E ;
C -- F ;
D -- E ;
E -- F ;
E -- G ;
}
```
.ordre() : Renvoie l'ordre du graphe.
.est_present() : renvoie True la valeur passée en paramètre est un des sommets du graphe, False sinon.
.degre() : renvoie le degré du sommet passé en paramètre.
Si ce sommet n'appartient pas au graphe, une erreur d'assertion doit survenir.
.voisins() : renvoie le tableau des voisins du sommet passé en paramètre.
Si ce sommet n'appartient pas au graphe, une erreur d'assertion doit survenir.
.sont_voisins() : renvoie True si les sommets passés en paramètres sont voisins l'un de l'autre, False sinon.
Si un des deux sommets n'appartient pas au graphe, une erreur d'assertion doit survenir.
.ajoute_sommet() : Ajoute le sommet passé en paramètre dans le graphe à condition que celui-ci ne soit pas déjà présent.
Cette méthode ne renvoie rien.
.supprime_sommet() : Supprime du graphe le sommet passé en paramètre (si celui-ci est présent).
Cette méthode ne renvoie rien.

Une piste
N'oubliez pas qu'un sommet peut être au départ et à l'arrivée d'une arête...
.ajoute_arete() : Cette fonction prend en paramètre un couple de sommets. Si le premier ou le second sommet ne sont pas présents dans le graphe, il y sont ajoutés puis l'arête entre les deux sommets est ajoutée à condition qu'elle ne soit pas déjà présente.
Cette méthode ne renvoie rien.

Une piste
N'oubliez pas qu'un sommet peu têtre au départ ou bien à l'arrivée d'un arc...
.supprime_arete() : Supprime l'arête correspondante du graphe. Cette méthode ne renvoie rien.
Si un des sommets n'appartient pas au graphe, ou si l'arête n'existe pas, des erreurs d'assertion doivent survenir.
Exemple d'utilisation
```
>>> G.supprime_arete( ('B', 'A') )
>>> print(G)
graph G {
B -- C ;
B -- G ;
C -- D ;
C -- E ;
C -- F ;
D -- E ;
E -- F ;
E -- G ;
}
```
.matrice() : renvoie la matrice d'adjacence du graphe, ainsi que le tableau des étiquettes des sommets afin de pouvoir établir une correspondance entre étiquette et indice dans la matrice.

TP - Implémenter une structure de graphe☘

Partie 1 - Classe GrapheOriente☘

Partie 2 - Classe Graphe☘

Partie 1 - Classe `GrapheOriente`☘

Partie 2 - Classe `Graphe`☘