Aller au contenu

Exercices pour s'entraîner☘

Prenez l'habitude de revenir vous entraîner régulièrement avec ces exercices tout au long de l'année.

Les exercices proposés dans cette page ont tous pour objectif d'implémenter une structure de graphe, de différentes manières. Les questions sont volontairement redondantes d'un exercice à l'autre et vous rappelleront le TP d'implémentation travaillé précédemment.

Vous vous limiterez toutefois à la programmation des méthodes non triviales. Libre à vous de programmer les autres ensuite.

Méthodes autorisées

Les méthodes usuelles sur les listes Python sont autorisées, à savoir :

  • .append() ;
  • .pop() ;
  • .remove() ;
  • .index() ;

ProgA05.51 - Graphe pondéré non orienté☘

Téléchargez le fichier « à trous » graphes_ponderes.py (clic droit -> [Enregistrer la cible du lien sous]) et enregistrez-le dans le dossier [Mes_modules].

Les objets de la classe GraphePondere sont munis d'un unique attribut : graphe_dico initialisé à None par défaut. Cet attribut est un dictionnaire contenant, pour chaque sommet du graphe, un dictionnaires dont les clefs sont les voisins du sommet et les valeurs sont les poids des arêtes correspondantes.

Exemple d'initialisation

Le graphe : 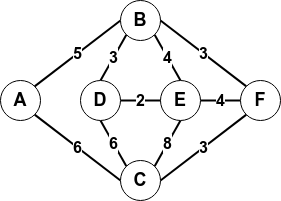Graphe pondéré sera implémenté de la façon suivante : 

1
2
3
4
5
6
7
L3 = {'A': {'B': 5, 'C': 6},
     'B': {'A': 5, 'D': 3, 'E': 4, 'F':3},
     'C': {'A': 6, 'D': 6, 'E': 8, 'F': 3},
     'D': {'B': 3, 'C': 6, 'E': 2},
     'E': {'B': 4, 'C': 8, 'D': 2, 'F': 4},
     'F': {'B': 3, 'C': 3, 'E': 4}}
G = GraphePondere(L3)

Complétez les méthodes de classe suivantes :

  1. .__init__() : initialisation de l'attribut graphe_dico.

    Une réponse
     6
 7
 8
 9
10
11
12
13
14
15
16
    def __init__(self, dico=None):
    """
    dico - dict, dictionnaire tel que:
           les clefs sont les sommets du graphe
           les valeurs sont un dictionnaire dont :
                les clefs sont les voisins du sommet
                les valeurs sont les poids des arêtes correspondantes
    """
    if dico is None:
        dico = {}
    self.graphe_dico = dico

  2. .sommets() : renvoie un tableau des sommets du graphe.

    Exemple de test

    >>> G.sommets()
['A', 'B', 'C', 'D', 'E', 'F']
    Une réponse
    18
19
    def sommets(self):
    return list(self.graphe_dico.keys())

  3. .aretes() : renvoie un tableau des arêtes du graphe. Ces arêtes sont définies sous la forme d'un couple (sommet_1, sommet_2).

    Exemple de test

    >>> G.aretes()
[('A', 'B'),
 ('A', 'C'),
 ('B', 'D'),
 ('B', 'E'),
 ('B', 'F'),
 ('C', 'D'),
 ('C', 'E'),
 ('C', 'F'),
 ('D', 'E'),
 ('E', 'F')]
    Une réponse
    21
22
23
24
25
26
27
28
29
30
    def aretes(self):
    """
    Sortie: tableau des arêtes, sans doublons
    """
    tab = []
    for s1 in self.graphe_dico.keys():
        for s2 in self.graphe_dico[s1].keys():
            if (s1, s2) not in tab and (s2, s1) not in tab :
                tab.append( (s1, s2) )
    return tab

  4. .aretes_ponderees() : renvoie un dictionnaire dont les clefs sont les arêtes du graphe et les valeurs sont les poids associés à ces arêtes.

    Exemple de test

    >>> G.aretes_ponderees()
{('A', 'B'): 5,
 ('A', 'C'): 6,
 ('B', 'D'): 3,
 ('B', 'E'): 4,
 ('B', 'F'): 3,
 ('C', 'D'): 6,
 ('C', 'E'): 8,
 ('C', 'F'): 3,
 ('D', 'E'): 2,
 ('E', 'F'): 4}
    Une réponse
    32
33
34
35
36
37
38
39
40
41
    def aretes_ponderees(self):
    """
    Sortie: dictionnaire dont les clefs sont les arêtes
            et dont les valeurs sont les poids associés
    """
    dico = {}
    for arete in self.aretes():
        (s1, s2) = arete
        dico[arete] = self.graphe_dico[s1][s2]
    return dico

  5. .__str__() : renvoie une chaîne de caractères compatible avec le logiciel Graphviz.

    Exemple d'affichage

    Avec l'exemple de graphe proposé au début de cette partie, on obtiendra l'affichage suivant : 

    >>> print(G)
graph G {
A -- B [label=5] ;
A -- C [label=6] ;
B -- D [label=3] ;
B -- E [label=4] ;
B -- F [label=3] ;
C -- D [label=6] ;
C -- E [label=8] ;
C -- F [label=3] ;
D -- E [label=2] ;
E -- F [label=4] ;
}

    Une réponse
    43
44
45
46
47
48
49
    def __str__(self):
    result = "graph G {\n"
    dico = self.aretes_ponderees()
    for arete in dico :
        (s1, s2) = arete
        result += f"{s1} -- {s2} [label={dico[arete]}] ;\n"
    return result+"}"

  6. .voisins() : renvoie le tableau des voisins du sommet passé en paramètre.
    Si ce sommet n'appartient pas au graphe, une erreur d'assertion doit survenir.

    Exemple de test

    >>> G.voisins('A')
['B', 'C']

>>> G.voisins('K')
AssertionError: le sommet K n'appartient pas au graphe
    Une réponse
    51
52
53
    def voisins(self, s):
    assert s in self.graphe_dico.keys(), f"le sommet {s} n'appartient pas au graphe"
    return list(self.graphe_dico[s].keys())

  7. .voisins_poids() : renvoie un dictionnaire dont les clefs sont les voisins du sommet passé en paramètre et les valeurs sont les poids associés.
    Si ce sommet n'appartient pas au graphe, une erreur d'assertion doit survenir.

    Exemple de test

    >>> G.voisins_poids('A')
{'B': 5, 'C': 6}

>>> G.voisins_poids('K')
AssertionError: le sommet K n'appartient pas au graphe
    Une réponse
    54
55
56
    def voisins_poids(self, s):
    assert s in self.graphe_dico.keys(), f"le sommet {s} n'appartient pas au graphe"
    return self.graphe_dico[s]

  8. .matrice() : renvoie la matrice de pondération du graphe, ainsi que le tableau des étiquettes des sommets afin de pouvoir établir une correspondance entre étiquette et indice dans la matrice.

    Exemple de test

    >>> tab, mat = G.matrice()
>>> print(tab)
['A', 'B', 'C', 'D', 'E', 'F']

>>> for ligne in mat:
...     print(ligne)
[0, 5, 6, 0, 0, 0]
[5, 0, 0, 3, 4, 3]
[6, 0, 0, 6, 8, 3]
[0, 3, 6, 0, 2, 0]
[0, 4, 8, 2, 0, 4]
[0, 3, 3, 0, 4, 0]
    Une réponse
    60
61
62
63
64
65
66
67
    def matrice(self):
    nb_sommets = len(self.graphe_dico)
    mat = [[0]*nb_sommets for i in range(nb_sommets)]
    tab_sommets = self.sommets()
    for i in range(nb_sommets):
        for sommet in self.graphe_dico[tab_sommets[i]]:
            mat[i][tab_sommets.index(sommet)] = self.graphe_dico[tab_sommets[i]][sommet]
    return tab_sommets, mat

ProgA05.52 - Graphe non pondéré défini par une matrice☘

Téléchargez le fichier « à trous » ProgA05.52.py (clic droit -> [Enregistrer la cible du lien sous]) et enregistrez-le dans le dossier [Mes_modules].

Les objets de la classe GrapheMatrice sont munis de deux attributs :

  • matrice qui est un tableau de tableaux d'entiers valant 0 ou 1.
    Ce tableau carré représente la matrice d'adjacence d'un graphe.
  • sommets qui est un tableau des étiquettes des sommets, initialisé à None par défaut. Cet attribut fait correspondre chaque indice de ligne de matrice à une étiquette. Si le tableau d'étiquette n'est pas fourni, les étiquettes seront les entiers de 0 à n-1, où n est le nombre de lignes de matrice.
Exemples d'initialisation

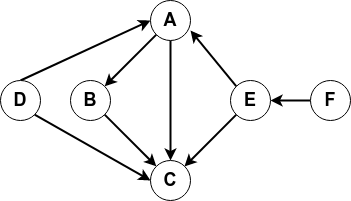Le graphe orienté : Graphe orienté sera implémenté de la façon suivante : 

1
2
3
4
5
6
7
8
9
M1 = [  [0, 1, 1, 0, 0, 0],
        [0, 0, 1, 0, 0, 0],
        [0, 0, 0, 0, 0, 0],
        [1, 0, 1, 0, 0, 0],
        [1, 0, 1, 0, 0, 0],
        [0, 0, 0, 0, 1, 0]]
sommets1 = ['A', 'B', 'C', 'D', 'E', 'F']

G1 = GrapheMatrice(M1, sommets1)

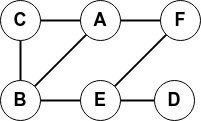Le graphe non orienté : Graphe orienté sera implémenté de la façon suivante : 

1
2
3
4
5
6
7
8
9
M2 = [  [0, 1, 1, 0, 0, 1],
        [1, 0, 1, 0, 1, 0],
        [1, 1, 0, 0, 0, 0],
        [0, 0, 0, 0, 1, 0],
        [0, 1, 0, 1, 0, 1],
        [1, 0, 0, 0, 1, 0]]
sommets2 = ['A', 'B', 'C', 'D', 'E', 'F']

G2 = GrapheMatrice(M2, sommets2)

Attention

La classe GrapheMatrice doit pouvoir être utilisée pour implémenter des graphes orientés comme non orientés.

Complétez les méthodes de classe suivantes :

  1. .__init__() : initialisation de l'attribut graphe_dico.
    Effectuez des tests d'assertion pour vérifier que la matrice est carrée et que le nombre d'étiquettes convient.

    Une réponse
     6
 7
 8
 9
10
11
12
13
14
15
16
17
18
    def __init__(self, matrice, tab_sommets=None):
    """
    matrice - list, tableau carré de n tableaux ayant n éléments
    tab_sommets - list, tableau des étiquettes des sommets,
                        entiers de 0 à n-1 par défaut
    """
    assert len(matrice) == len(matrice[0]), "La matrice n'est pas carrée"
    self.matrice = matrice
    if tab_sommets is None:
        self.sommets = list(range(len(matrice)))
    else:
        self.sommets = tab_sommets
    assert len(self.matrice) == len(self.sommets), "Le nombre de sommets de convient pas"

  2. .est_oriente() : renvoie True si la matrice est celle d'un graphe orienté, False sinon.

    Exemple de test

    >>> G1.est_oriente()
True

>>> G2.est_oriente()
False
    Une réponse
    21
22
23
24
25
26
    def est_oriente(self):
    for i in range(len(self.matrice)):
        for j in range(i, len(self.matrice)):
            if self.matrice[i][j] != self.matrice[j][i]:
                return True
    return False

  3. .indices_sommets() : renvoie un dictionnaire qui, à chaque indice, associe l'étiquette correspondante.

    Exemple de test

    >>> G1.indices_sommets()
{0: 'A', 1: 'B', 2: 'C', 3: 'D', 4: 'E', 5: 'F'}
    Une réponse
    18
19
    def indices_sommets(self):
    return {i: self.sommets[i] for i in range(len(self.sommets))}

  4. Il faut programmer des fonctions permettant de renvoyer le tableau des arêtes dans le cas d'un graphe non orienté, et des arcs dans le cas d'un graphe orienté.

    1. .aretes() : renvoie un tableau des arêtes du graphe.
      Ces arêtes sont définies sous la forme d'un couple (sommet_1, sommet_2).
      Un test d'assertion est nécessaire pour le cas où cette méthode est appelée sur un graphe orienté.

      Exemple de test

      >>> G1.aretes()
AssertionError: Le graphe est orienté, il a des arcs, pas des arêtes

>>> G2.aretes()
[('A', 'B'),
 ('A', 'C'),
 ('A', 'F'),
 ('B', 'C'),
 ('B', 'E'),
 ('D', 'E'),
 ('E', 'F')]

    2. .arcs() : renvoie un tableau des arcs du graphe.
      Ces arcs sont définis sous la forme d'un couple (sommet_1, sommet_2).
      Un test d'assertion est nécessaire pour le cas où cette méthode est appelée sur un graphe non orienté.

      Exemple de test

      >>> G1.arcs()
[('A', 'B'),
 ('A', 'C'),
 ('B', 'C'),
 ('D', 'A'),
 ('D', 'C'),
 ('E', 'A'),
 ('E', 'C'),
 ('F', 'E')]

>>> G2.arcs()
AssertionError: Le graphe n'est pas orienté, il a des arêtes, pas des arcs

    3. Une proposition de solution, qui évite des copier/coller de code.

      Une réponse
      33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
      def liaisons(self, oriente):
    tab = []
    for i in range(len(self.matrice)):
        for j in range(len(self.matrice[0])):
            if self.matrice[i][j] != 0:
                if oriente or (not oriente and j>i) :
                    tab.append( (self.sommets[i], self.sommets[j]) )
    return tab


def aretes(self):
    """
    Sortie: tableau des arêtes, sans doublons
    """
    assert not self.est_oriente(), "Le graphe est orienté, il a des arcs, pas des arêtes"
    return self.liaisons(False)


def arcs(self):
    """
    Sortie: tableau des arcs dans le cas d'un graphe orienté
    """
    assert self.est_oriente(), "Le graphe n'est pas orienté, il a des arêtes, pas des arcs"
    return self.liaisons(True)

  5. .__str__() : renvoie une chaîne de caractères compatible avec le logiciel Graphviz.

    Exemple d'affichage

    >>> print(G1)
digraph G {
A -> B ;
A -> C ;
B -> C ;
D -> A ;
D -> C ;
E -> A ;
E -> C ;
F -> E ;
}

>>> print(G2)
graph G {
A -- B ;
A -- C ;
A -- F ;
B -- C ;
B -- E ;
D -- E ;
E -- F ;
}
    Une réponse
    59
60
61
62
63
64
65
66
67
68
69
70
    def __str__(self):
    oriente = self.est_oriente()

    if oriente:
        result = "digraph G {\n"
        fleche = "->"
    else:
        result = "graph G {\n"
        fleche = "--"
    for arete in self.liaisons(oriente):
        result += f"{arete[0]} {fleche} {arete[1]} ;\n"
    return result+"}"

  6. Il faut programmer des fonctions permettant de renvoyer les dictionnaires des voisins, des successeurs, selon le type de graphe.

    1. .voisins() : renvoie le tableau des voisins du sommet passé en paramètre.
      Un test d'assertion est nécessaire pour le cas où cette méthode est appelée sur un graphe orienté.

      Exemple de test

      >>> G1.voisins('A')
AssertionError: Le graphe est orienté, recherchez plutôt les successeurs (ou prédécesseurs)

>>> G2.voisins('A')
['B', 'C', 'F']

    2. .successeurs() : renvoie le tableau des successeurs du sommet passé en paramètre.
      Un test d'assertion est nécessaire pour le cas où cette méthode est appelée sur un graphe non orienté.

      Exemple de test

      >>> G1.successeurs('A')
['B', 'C']

>>> G2.successeurs('A')
AssertionError: Le graphe n'est pas orienté, recherchez plutôt les voisins

    3. Une proposition de solution, qui évite des copier/coller de code.

      Une réponse
      33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
      def relies_a(self, s):
    assert s in self.sommets, f"le sommet {s} n'appartient pas au graphe"
    indice = self.sommets.index(s)
    tab = []
    for i in range(len(self.matrice[indice])):
        if self.matrice[indice][i] != 0:
            tab.append(self.sommets[i])
    return tab


def voisins(self, s):
    assert not self.est_oriente(), "Le graphe est orienté, recherchez plutôt les successeurs (ou prédécesseurs)"
    return self.relies_a(s)


def successeurs(self, s):
    assert self.est_oriente(), "Le graphe n'est pas orienté, recherchez plutôt les voisins"
    return self.relies_a(s)

  7. .predecesseurs() : renvoie le tableau des prédécesseurs du sommet passé en paramètre.
    Un test d'assertion est nécessaire pour le cas où cette méthode est appelée sur un graphe non orienté.

    Exemple de test

    >>> G1.predecesseurs('A')
['D', 'E']

>>> G2.predecesseurs('A')
AssertionError: Le graphe n'est pas orienté, recherchez plutôt les voisins
    Une réponse
     93
 94
 95
 96
 97
 98
 99
100
101
    def predecesseurs(self, s):
    assert self.est_oriente(), "Le graphe n'est pas orienté, recherchez plutôt les voisins"
    assert s in self.sommets, f"le sommet {s} n'appartient pas au graphe"
    indice = self.sommets.index(s)
    tab = []
    for i in range(len(self.matrice[indice])):
        if self.matrice[i][indice] != 0:
            tab.append(self.sommets[i])
    return tab

  8. .dico_voisins() : renvoie un dictionnaire dont les clefs sont les sommets du graphe et les valeurs associées sont les voisins de ce sommet dans le cas d'un graphe non orienté et les successeurs de ce sommet dans le cas d'un graphe orienté.

    Exemple de test

    >>> G1.dico_voisins()
{'A': ['B', 'C'],
 'B': ['C'],
 'C': [],
 'D': ['A', 'C'],
 'E': ['A', 'C'],
 'F': ['E']}

>>> G2.dico_voisins()
{'A': ['B', 'C', 'F'],
 'B': ['A', 'C', 'E'],
 'C': ['A', 'B'],
 'D': ['E'],
 'E': ['B', 'D', 'F'],
 'F': ['A', 'E']}
    Une réponse
    104
105
106
107
108
109
110
111
    def dico_voisins(self):
    dico = {}
    for i in range(len(self.matrice)):
        dico[self.sommets[i]] = []
        for j in range(len(self.matrice[0])):
            if self.matrice[i][j] != 0:
                dico[self.sommets[i]].append(self.sommets[j])
    return dico
    Une autre réponse
    104
105
106
107
108
109
    def dico_voisins2(self):
    dico = {}
    oriente = self.est_oriente()
    for sommet in self.sommets:
        dico[sommet] = self.relies_a(sommet)
    return dico

ProgA05.53 - Graphe pondéré défini par une matrice☘

Téléchargez le fichier « à trous » ProgA05.53.py (clic droit -> [Enregistrer la cible du lien sous]) et enregistrez-le dans le dossier [Mes_modules].

Les objets de la classe GrapheMatricePondere sont munis de deux attributs :

  • matrice qui est un tableau de tableaux d'entiers .
    Ce tableau carré représente la matrice de pondération d'un graphe.
  • sommets qui est un tableau des étiquettes des sommets, initialisé à None par défaut. Cet attribut fait correspondre chaque indice de ligne de matrice à une étiquette. Si le tableau d'étiquette n'est pas fourni, les étiquettes seront les entiers de 0 à n-1, où n est le nombre de lignes de matrice.
Exemple d'initialisation

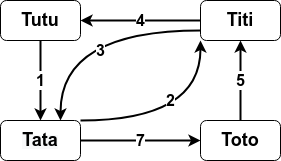Le graphe orienté : Graphe orienté sera implémenté de la façon suivante : 

1
2
3
4
5
6
7
M3 = [  [0, 2, 7, 0],
        [3, 0, 0, 4],
        [0, 5, 0, 0],
        [1, 0, 0, 0]]
sommets3 = ['Tata', 'Titi', 'Toto', 'Tutu']

G3 = GrapheMatricePondere(M3, sommets3)

Le graphe non orienté : Graphe orienté sera implémenté de la façon suivante : 

1
2
3
4
5
6
7
8
9
M4 = [  [0, 5, 6, 0, 0, 0],
        [5, 0, 0, 3, 4, 3],
        [6, 0, 0, 6, 8, 3],
        [0, 3, 6, 0, 2, 0],
        [0, 4, 8, 2, 0, 4],
        [0, 3, 3, 0, 4, 0]]
sommets4 = ['A', 'B', 'C', 'D', 'E', 'F']

G4 = GrapheMatricePondere(M4, sommets4)

Attention

La classe GrapheMatricePondere doit pouvoir être utilisée pour implémenter des graphes orientés comme non orientés.

Complétez les méthodes de classe du programme en adaptant le code réalisé dans l'exercice précédent.

  1. .__init__() : initialisation de l'attribut graphe_dico.
    Effectuez des tests d'assertion pour vérifier que la matrice est carrée et que le nombre d'étiquettes convient.

  2. .est_oriente() : renvoie True si la matrice est celle d'un graphe orienté, False sinon.

    Exemple de test

    >>> G3.est_oriente()
True

>>> G4.est_oriente()
False

  3. .indices_sommets() : renvoie un dictionnaire qui, à chaque indice, associe l'étiquette correspondante.

    Exemple de test

    >>> G3.indices_sommets()
{0: 'Tata', 1: 'Titi', 2: 'Toto', 3: 'Tutu'}

  4. Il faut programmer des fonctions permettant de renvoyer le tableau des arêtes dans le cas d'un graphe non orienté, et des arcs dans le cas d'un graphe orienté.

    1. .aretes() : renvoie un dictionnaire dont les clefs sont les arêtes du graphe et les valeurs sont les pondérations associées à cette arête.
      Ces arêtes sont définies sous la forme d'un couple (sommet_1, sommet_2).
      Un test d'assertion est nécessaire pour le cas où cette méthode est appelée sur un graphe orienté.

      Exemple de test

      >>> G3.aretes()
AssertionError: Le graphe est orienté, il a des arcs, pas des arêtes

>>> G4.aretes()
{('A', 'B'): 5,
 ('A', 'C'): 6,
 ('B', 'D'): 3,
 ('B', 'E'): 4,
 ('B', 'F'): 3,
 ('C', 'D'): 6,
 ('C', 'E'): 8,
 ('C', 'F'): 3,
 ('D', 'E'): 2,
 ('E', 'F'): 4}

    2. .arcs() : renvoie un dictionnaire dont les clefs sont les arcs du graphe et les valeurs sont les pondérations associées à cet arc.
      Ces arcs sont définis sous la forme d'un couple (sommet_1, sommet_2).
      Un test d'assertion est nécessaire pour le cas où cette méthode est appelée sur un graphe non orienté.

      Exemple de test

      >>> G3.arcs()
{('Tata', 'Titi'): 2,
 ('Tata', 'Toto'): 7,
 ('Titi', 'Tata'): 3,
 ('Titi', 'Tutu'): 4,
 ('Toto', 'Titi'): 5,
 ('Tutu', 'Tata'): 1}

>>> G4.arcs()
AssertionError: Le graphe n'est pas orienté, il a des arêtes, pas des arcs

  5. .__str__() : renvoie une chaîne de caractères compatible avec le logiciel Graphviz.

    Exemple d'affichage

    >>> print(G3)
digraph G {
Tata -> Titi [label=2] ;
Tata -> Toto [label=7] ;
Titi -> Tata [label=3] ;
Titi -> Tutu [label=4] ;
Toto -> Titi [label=5] ;
Tutu -> Tata [label=1] ;
}

>>> print(G4)
graph G {
A -- B [label=5] ;
A -- C [label=6] ;
B -- D [label=3] ;
B -- E [label=4] ;
B -- F [label=3] ;
C -- D [label=6] ;
C -- E [label=8] ;
C -- F [label=3] ;
D -- E [label=2] ;
E -- F [label=4] ;
}

  6. Il faut programmer des fonctions permettant de renvoyer les dictionnaires des voisins, des successeurs, selon le type de graphe.

    1. .voisins() : renvoie le tableau des voisins du sommet passé en paramètre.
      Un test d'assertion est nécessaire pour le cas où cette méthode est appelée sur un graphe orienté.

      Exemple de test

      >>> G3.voisins('Toto')
AssertionError: Le graphe est orienté, recherchez plutôt les successeurs (ou prédécesseurs)

>>> G4.voisins('Toto')
AssertionError: le sommet Toto n'appartient pas au graphe

>>> G4.voisins('A')
['B', 'C']

    2. .successeurs() : renvoie le tableau des successeurs du sommet passé en paramètre.
      Un test d'assertion est nécessaire pour le cas où cette méthode est appelée sur un graphe non orienté.

      Exemple de test

      >>> G3.successeurs('A')
AssertionError: le sommet A n'appartient pas au graphe

>>> G3.successeurs('Tata')
['Titi', 'Toto']

>>> G4.successeurs('A')
AssertionError: Le graphe n'est pas orienté, recherchez plutôt les voisins

  7. .predecesseurs() : renvoie le tableau des prédécesseurs du sommet passé en paramètre.
    Un test d'assertion est nécessaire pour le cas où cette méthode est appelée sur un graphe non orienté.

    Exemple de test

    >>> G3.predecesseurs('Tata')
['Titi', 'Tutu']

>>> G4.predecesseurs('A')
AssertionError: Le graphe n'est pas orienté, recherchez plutôt les voisins

  8. .dico_voisins() : renvoie un dictionnaire dont les clefs sont les sommets du graphe et les valeurs associées sont les dictionnaires associant les voisins (les successeurs dans le cas d'un graphe orienté) de ce sommet, eux-mêmes associés au poids de l'arête (de l'arc) les reliant. dans le cas d'un graphe non orienté et les successeurs de ce sommet.

    Exemple de test

    >>> G3.dico_voisins()
{'Tata': {'Titi': 2, 'Toto': 7},
 'Titi': {'Tata': 3, 'Tutu': 4},
 'Toto': {'Titi': 5},
 'Tutu': {'Tata': 1}}

>>> G4.dico_voisins()
{'A': {'B': 5, 'C': 6},
 'B': {'A': 5, 'D': 3, 'E': 4, 'F': 3},
 'C': {'A': 6, 'D': 6, 'E': 8, 'F': 3},
 'D': {'B': 3, 'C': 6, 'E': 2},
 'E': {'B': 4, 'C': 8, 'D': 2, 'F': 4},
 'F': {'B': 3, 'C': 3, 'E': 4}}

Une proposition de solution☘

Une réponse
  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
class GrapheMatricePondere:
    """Implémentation de graphes pondérés, orientés ou non, à l'aide d'une
    matrice de pondération"""

    def __init__(self, matrice, tab_sommets=None):
        """
        matrice - list, tableau carré de n tableaux ayant n éléments
        tab_sommets - list, tableau des étiquettes des sommets,
                            entiers de 0 à n-1 par défaut
        """
        assert len(matrice) == len(matrice[0]), "La matrice n'est pas carrée"
        self.matrice = matrice
        if tab_sommets is None:
            self.sommets = list(range(len(matrice)))
        else:
            self.sommets = tab_sommets
        assert len(self.matrice) == len(self.sommets), "Le nombre de sommets ne convient pas"


    def est_oriente(self):
        for i in range(len(self.matrice)):
            for j in range(i, len(self.matrice)):
                if self.matrice[i][j] != self.matrice[j][i]:
                    return True
        return False


    def indices_sommets(self):
        return {i: self.sommets[i] for i in range(len(self.sommets))}


    def liaisons(self, oriente):
        dico = {}
        for i in range(len(self.matrice)):
            for j in range(len(self.matrice[0])):
                if self.matrice[i][j] != 0:
                    if oriente or (not oriente and j>i) :
                        dico[(self.sommets[i], self.sommets[j])] = self.matrice[i][j]
        return dico


    def aretes(self):
        """
        Sortie: tableau des arêtes, sans doublons
        """
        assert not self.est_oriente(), "Le graphe est orienté, il a des arcs, pas des arêtes"
        return self.liaisons(False)


    def arcs(self):
        """
        Sortie: tableau des arcs dans le cas d'un graphe orienté
        """
        assert self.est_oriente(), "Le graphe n'est pas orienté, il a des arêtes, pas des arcs"
        return self.liaisons(True)


    def __str__(self):
        oriente = self.est_oriente()

        if oriente:
            result = "digraph G {\n"
            fleche = "->"
        else:
            result = "graph G {\n"
            fleche = "--"
        liens = self.liaisons(oriente)
        for arete in liens.keys():
            result += f"{arete[0]} {fleche} {arete[1]} [label={liens[arete]}] ;\n"
        return result+"}"


    def relies_a(self, s):
        assert s in self.sommets, f"le sommet {s} n'appartient pas au graphe"
        indice = self.sommets.index(s)
        tab = []
        for i in range(len(self.matrice[indice])):
            if self.matrice[indice][i] != 0:
                tab.append(self.sommets[i])
        return tab


    def voisins(self, s):
        assert not self.est_oriente(), "Le graphe est orienté, recherchez plutôt les successeurs (ou prédécesseurs)"
        return self.relies_a(s)


    def successeurs(self, s):
        assert self.est_oriente(), "Le graphe n'est pas orienté, recherchez plutôt les voisins"
        return self.relies_a(s)


    def predecesseurs(self, s):
        assert self.est_oriente(), "Le graphe n'est pas orienté, recherchez plutôt les voisins"
        assert s in self.sommets, f"le sommet {s} n'appartient pas au graphe"
        indice = self.sommets.index(s)
        tab = []
        for i in range(len(self.matrice[indice])):
            if self.matrice[i][indice] != 0:
                tab.append(self.sommets[i])
        return tab


    def dico_voisins(self):
        dico = {}
        for i in range(len(self.matrice)):
            dico[self.sommets[i]] = {}
            for j in range(len(self.matrice[0])):
                if self.matrice[i][j] != 0:
                    dico[self.sommets[i]][self.sommets[j]] = self.matrice[i][j]
        return dico



if __name__ == "__main__":
    print("Tests pour un graphe orienté")
    M3 = [  [0, 2, 7, 0],
            [3, 0, 0, 4],
            [0, 5, 0, 0],
            [1, 0, 0, 0]]
    sommets3 = ['Tata', 'Titi', 'Toto', 'Tutu']

    G3 = GrapheMatricePondere(M3, sommets3)

    print(G3.est_oriente())
    print(G3.indices_sommets())
    print(G3.arcs())
    print(G3)
    print()
    for sommet in sommets3:
        print(sommet, G3.successeurs(sommet))
        print(sommet, G3.predecesseurs(sommet))
        print()
    print(G3.dico_voisins())
    print()

    print("Tests pour un graphe non orienté")
    M4 = [  [0, 5, 6, 0, 0, 0],
            [5, 0, 0, 3, 4, 3],
            [6, 0, 0, 6, 8, 3],
            [0, 3, 6, 0, 2, 0],
            [0, 4, 8, 2, 0, 4],
            [0, 3, 3, 0, 4, 0]]
    sommets4 = ['A', 'B', 'C', 'D', 'E', 'F']

    G4 = GrapheMatricePondere(M4, sommets4)

    print(G4.est_oriente())
    print(G4.indices_sommets())
    print(G4.aretes())
    print(G4)
    print()
    for sommet in sommets4:
        print(sommet, G4.voisins(sommet))
        print()
    print(G4.dico_voisins())