Exercices pour approfondir

Ces exercices doivent être utilisés pour approfondir votre maîtrise de la programmation. Ils sont parfois accompagnés d'aide et de leur solution pour vous permettre de progresser.

Avant de vous précipiter sur ces solutions dès la première difficulté, n'oubliez pas les conseils suivants :

• Avez-vous bien fait un schéma au brouillon pour visualiser le problème posé ?
• Avez-vous essayé de rédiger un algorithme en français, avec vos propres mots, avant de vous lancer dans la programmation sur machine ?
• Avez-vous utilisé des affichages intermédiaires, des print(), pour visualiser au fur et à mesure le contenu des variables ?
• Avez-vous testé le programme avec les propositions de tests donnés dans l'exercice ?
• Avez-vous testé le programme avec de nouveaux tests, différents de ceux proposés ?

Rappels

• Chaque programme Python doit être sauvegardé sous forme de fichier texte avec l'extension .py.
  Enregistrez ce fichier dans le dossier [F01-Bases de programmation] avec le nom donné à l'exercice : ProgF01.61.py, ProgF01.62.py, etc...
• Pour exécuter ce programme, il suffit de le sauvegarder puis d'appuyer sur la touche [F5].

ProgF01.61

Copiez/collez et complétez le corps de la fonction val_abs_diff() en respectant ses spécifications.

def val_abs_diff(a, b):
    """
    a, b - int ou float
    Sortie: int ou float – la valeur absolue de (a-b)
    """

Proposition de tests

>>> val_abs_diff(3, 5)
2

>>> val_abs_diff(5.7, 2.9)
2.8

Une piste

Si vous ne vous rappelez pas ce qu'est la valeur absolue d'une expression, vous pouvez recommencer cet exercice.

Une solution

def val_abs_diff(a, b):
    """
    a, b - int ou float
    Sortie: int ou float – la valeur absolue de (a-b)
    """
    if a-b >= 0 :
        return a-b
    else:
        return b-a

ProgF01.62

Définissez la fonction eq_2nd_degre() qui résout l'équation du 2nd degré $a x^2 + b x + c = 0$, avec $a \neq 0$. Cette fonction renverra :

• None si l'équation n'a pas de solution ;
• la valeur de l'unique solution s'il n'y en a qu'une ;
• la valeur des deux solutions s'il y en a deux.

Le module math contient les fonctions usuelles de mathématiques. Une fois ce module importé, la fonction sqrt() calcule la racine carrée d'un nombre de type int ou float. Cette fonction sqrt() renvoie un float.

Une piste

Ouvrir son cahier de spécialité mathématiques semble une bonne idée...

Une proposition de spécification

def eq_2nd_degre(a, b, c):
    """
    a – int ou float, non nul
    b, c – int ou float
    Sortie: None ou float ou (float, float)
            None si ax² + bx + c = 0 n'a pas de solution
            float si ax² + bx + c = 0 a une solution
            (float, float) si ax² + bx + c = 0 a deux solutions
    """

Tests de vérification

>>> eq_2nd_degre(1, 2, 1)
-1.0

>>> eq_2nd_degre(1, 2, 3)


>>> eq_2nd_degre(1, 1, -6)
(-3.0, 2.0)

Une solution

Ne pas oublier d'importer la fonction racine carrée module math...

from math import sqrt
def eq_2nd_degre(a, b, c):
    """
    a – int ou float, non nul
    b, c – int ou float
    Sortie: None ou float ou (float, float)
            None si ax² + bx + c = 0 n'a pas de solution
            float si ax² + bx + c = 0 a une solution
            (float, float) si ax² + bx + c = 0 a deux solutions
    """
    delta = b*b-4*a*c
    if delta < 0:
        return None
    elif delta == 0:
        return -b/(2*a)
    else:
        x1 = (-b-sqrt(delta))/(2*a)
        x2 = (-b+sqrt(delta))/(2*a)
        return x1, x2

ProgF01.63

Les années bissextiles sont les années divisibles par 4, à l'exception de celles qui sont divisibles par 100 sans l'être par 400. Par exemple :

• 2000 est une année bissextile (2000 est divisible par 4. 2000 est divisible par 100 mais aussi par 400 : il ne fait donc pas partie des exceptions).
• 2012 est divisible par 4 mais pas par 100 : 2012 est bissextile.
• 1900 est divisible par 4, par 100 mais pas par 400 : 1900 n'est pas bissextile.

Définissez la fonction bissextile() dont le paramètre est un entier naturel non nul (l'année) puis qui renvoie True lorsque l'année est bissextile ou False dans le cas contraire.

Proposition de tests

>>> bissextile(2000)
True

>>> bissextile(2012)
True

>>> bissextile(1900)
False

Une piste

Un entier n est divisible par un entier d si le reste de la division de n par d est nul.
En langage Python, cela signifie que n%d doit être égal à 0...

Une autre piste

Il faut apprendre à tracer ce type de schéma avant de se lancer dans l'écriture d'un programme !

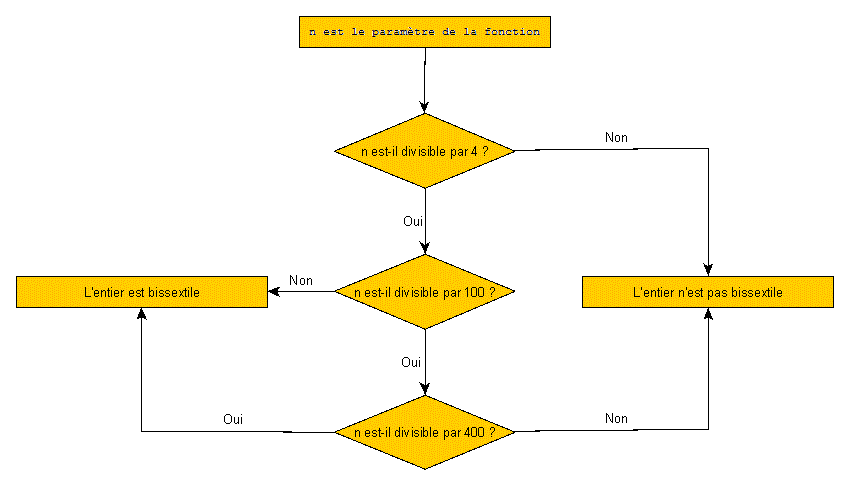
Une proposition de spécification

Par rapport au schéma, on renomme le paramètre afin que ce nom soit plus pertinent.

def bissextile(annee):
    """
    annee – int, entier strictement positif
    Sortie: bool - True si annee est bissextile, False sinon
    """

Une solution

def bissextile(annee):
    """
    annee – int, entier strictement positif
    Sortie: bool - True si annee est bissextile, False sinon
    """
    if annee%4 != 0 :                               # Pas divisible par 4
        return False
    elif (annee%100 == 0) and (annee%400 != 0):     # divisible par 100 et pas par 400
        return False
    else :
        return True        

ProgF01.64

Définissez la fonction ordre3() dont les trois paramètres sont numériques et qui renvoie ces trois paramètres, du plus petit au plus grand.

Proposition de tests

>>> ordre3(3, 5, 4)
(3, 4, 5)

>>> ordre3(9, 6, 3)
(3, 6, 9)

>>> ordre3(1, 2, 3)
(1, 2, 3)

Une piste

Vous pouvez utiliser les affectations parallèles pour échanger les valeurs des variables :

a, b = b, a

Une proposition de spécification

def ordre3(a, b, c):
    """
    a, b, c – int ou float
    Sortie: triplet de trois éléments - a, b et c classés du plus petit au plus grand
    """

Une solution

def ordre3(a, b, c):
    """
    a, b, c – int ou float
    Sortie: tuple de trois éléments - a, b et c classés du plus petit au plus grand
    """
    if a > b :
        a, b = b, a                 # a est forcément plus petit que b
    if b > c :
        b, c = c, b                 # c est forcément plus grand que b
    if a > b :
        a, b = b, a                 # a est forcément plus petit que (le nouveau) b
    return a, b, c

Une variante bien trop longue

Cependant, si vous avez programmé cela, c'est une bonne base en début d'année. Essayez de bien comprendre la solution précédente pour vous améliorer.

def ordre3(a, b, c):
    """
    a, b, c – int ou float
    Sortie: tuple de trois éléments - a, b et c classés du plus petit au plus grand
    """
    if a < b :
        if b < c :
            return a, b, c
        elif a < c:
            return a, c, b
        else:
            return c, a, b
    else:
        if a < c :
            return b, a, c
        elif b < c:
            return b, c, a
        else:
            return c, b, a

ProgF01.65

On appelle « nombres de Fibonacci » les nombres obtenus par somme des deux précédents.

Les deux premiers nombres de Fibonacci sont $F_0 = 1$ et $F_1 = 1$.
On a ensuite $F_2 = 2$, $F_3 = 3$, $F_4 = 5$, $F_5 = 8$, $F_6 = 13$, etc...

Complétez le corps de la fonction fibo() en respectant ses spécifications.

def fibo(n):
    """
    n – int, entier positif
    Sortie: int – le n-ième nombre de Fibonacci
    """

Tests de vérification

>>> fibo(0)
1

>>> fibo(1)
1

>>> fibo(6)
13

Une solution

def fibo(n):
    """
    n – int, entier positif
    Sortie: int – le n-ième nombre de Fibonacci
    """
    if (n == 0) or (n == 1):
        return 1
    else:
        f_ancien = 1
        f_actuel = 1
        for i in range(2, n+1):
            f_nouveau = f_ancien + f_actuel
            f_ancien = f_actuel
            f_actuel = f_nouveau
        return f_nouveau

ProgF01.66

Définir la fonction som_sup() qui prend pour paramètre un entier naturel A et qui renvoie le plus petit entier n tel que la somme S = 0+1+2+...+n soit supérieure ou égale à A.

Une proposition de spécification

def som_sup(A):
    """
    A – int, entier positif ou nul
    Sortie: int - le plus petit entier n tel que 0+1+2+...+n est supérieur ou égal à A
    """

Tests de vérification

>>> som_sup(17)
6

>>> som_sup(102587)
453

Une solution

def som_sup(A):
    """
    A – int, entier positif ou nul
    Sortie: int - le plus petit entier n tel que 0+1+2+...+n est supérieur ou égal à A
    """
    somme = 0
    compteur = 0
    while somme < A:
        compteur = compteur + 1
        somme = somme + compteur
    return compteur