Aller au contenu

Carrés magiques☘

L'exemple suivant est extrait d'une page wikipedia :

Définition

Cette page donne la définition suivante :

  • Un carré magique d’ordre n est composé de n^2 entiers strictement positifs distincts, écrits sous la forme d’un tableau carré.
  • Ces nombres sont disposés de sorte que les sommes sur chaque rangée, sur chaque colonne et sur chaque diagonale principale soient égales.
  • On nomme alors constante magique la valeur de ces sommes.

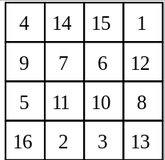
Un exemple de carré magique 4×4 extrait de la même page :

Téléchargez le fichier « à trous » ProgB05.60.py (clic droit -> [Enregistrer sous]) et enregistrez-le dans le dossier [B05_Tableaux_de_Tableaux].

Ajoutez ensuite des tests personnalisés dans la partie principale du programme.

Rappels
  • Enregistrez le fichier à compléter dans le dossier [B05-Tableaux_de_Tableaux] avec le nom donné à l'exercice : ProgB05.60.py.
  • Pour exécuter ce programme, il suffit de le sauvegarder puis d'appuyer sur la touche [F5].
  • Le programme principal doit contenir un appel au module doctest : 
    ##----- Programme principal et tests -----##
if __name__ == '__main__':
    import doctest
    doctest.testmod()

Partie 1 - Une matrice est-elle carrée ?☘

Complétez la définition de la fonction suivante en respectant ses spécifications.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
def est_carree(matrice):
    """
    matrice - list, Tableau de tableaux
    Sortie: bool - renvoie True si matrice est carrée
            (même nombre de lignes et de colonnes), False sinon.
    >>> A = [[1, 2], [3, 4], [5, 6]]
    >>> est_carree(A)
    False
    >>> B = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
    >>> est_carree(B)
    True
    >>> C = [[1, 2, 3], [4, 5, 6], [7, 8]]
    >>> est_carree(C)
    False
    """
Une solution
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
def est_carree(matrice):
    """
    matrice - list, Tableau de tableaux
    Sortie: bool - renvoie True si matrice est carrée
            (même nombre de lignes et de colonnes), False sinon.
    >>> A = [[1, 2], [3, 4], [5, 6]]
    >>> est_carree(A)
    False
    >>> B = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
    >>> est_carree(B)
    True
    >>> C = [[1, 2, 3], [4, 5, 6], [7, 8]]
    >>> est_carree(C)
    False
    """
    nb_lignes = len(matrice)
    for num_ligne in range(nb_lignes):
        nb_colonnes = len(matrice[num_ligne])
        if nb_colonnes != nb_lignes:
            return False
    return True

Partie 2 - Tous les éléments sont-ils distincts ?☘

Complétez la définition de la fonction suivante en respectant ses spécifications.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
def tous_distincts(matrice):
    """
    matrice - list, matrice carrée
    Sortie: bool - renvoie True si tous les éléments des sous-tableaux
            de matrice sont distincts, False sinon.
    >>> A = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
    >>> tous_distincts(A)
    True
    >>> B = [[1, 2, 3], [4, 5, 2], [3, 8, 9]]
    >>> tous_distincts(B)
    False
    """
Une solution
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
def tous_distincts(matrice):
    """
    matrice - list, matrice carrée
    Sortie: bool - renvoie True si tous les éléments des sous-tableaux
            de matrice sont distincts, False sinon.
    >>> A = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
    >>> tous_distincts(A)
    True
    >>> B = [[1, 2, 3], [4, 5, 2], [3, 8, 9]]
    >>> tous_distincts(B)
    False
    """
    liste_elements = []
    for ligne in matrice:
        for element in ligne:
            if element not in liste_elements:
                liste_elements.append(element)
            else:
                return False
    return True

Partie 3 - Le carré est-il magique ?☘

CComplétez la définition de la fonction suivante en respectant ses spécifications.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
def est_magique(matrice):
    """
    matrice - list, matrice carrée d'entiers tous distincts
    Sortie: bool - renvoie True si matrice est un carré magique, False sinon.
    >>> A = [[2, 7, 6], [9, 5, 1], [4, 3, 8]]
    >>> est_magique(A)
    True
    >>> B = [[4, 14, 15, 1], [9, 7, 6, 12], [5, 11, 10, 8], [16, 2, 3, 13]]
    >>> est_magique(B)
    True
    >>> C = [[4, 14, 15, 1], [9, 7, 6, 12], [5, 11, 10, 8], [2, 3, 13, 16]]
    >>> est_magique(C)
    False
    """
Une piste

Pensez à définir des fonctions auxiliaires pour calculer séparément :

  • les sommes des termes d'une ligne,
  • les sommes des termes d'une colonne,
  • les sommes des termes de la première diagonale,
  • les sommes des termes de la seconde diagonale.
Un code possible
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
def somme_ligne(ligne):
    """
    ligne - list, tableau d'entiers
    Sortie: int - somme des entiers de ligne
    """   
    somme = 0
    for valeur in ligne:
        somme += valeur
    return somme


def somme_colonne(matrice, num_colonne):
    """
    matrice - matrice carrée d'entiers
    num_colonne - int, entier tel que 0 <= num_colonne < len(matrice)
    Sortie: int - somme des entiers de la colonne num_colonne de matrice
    """   
    somme = 0
    for ligne in matrice:
        somme += ligne[num_colonne]
    return somme


def somme_diagonale_NO_SE(matrice):
    """
    matrice - matrice carrée d'entiers
    Sortie: int - somme des entiers de la diagonale \
    """   
    somme = 0
    n = len(matrice)
    for i in range(n):
        somme += matrice[i][i]
    return somme


def somme_diagonale_SO_NE(matrice):
    """
    matrice - matrice carrée d'entiers
    Sortie: int - somme des entiers de la diagonale /
    """   
    somme = 0
    n = len(matrice)
    for i in range(n):
        somme += matrice[i][n-1-i]
    return somme



def est_magique(matrice):
    """
    matrice - list, matrice carrée d'entiers tous distincts
    Sortie: bool - renvoie True si matrice est un carré magique, False sinon.
    >>> A = [[2, 7, 6], [9, 5, 1], [4, 3, 8]]
    >>> est_magique(A)
    True
    >>> B = [[4, 14, 15, 1], [9, 7, 6, 12], [5, 11, 10, 8], [16, 2, 3, 13]]
    >>> est_magique(B)
    True
    >>> C = [[4, 14, 15, 1], [9, 7, 6, 12], [5, 11, 10, 8], [2, 3, 13, 16]]
    >>> est_magique(C)
    False
    """
    n = len(matrice)        # nombre de lignes de matrice
    constante_magique = somme_ligne(matrice[0])
    for k in range(1, n):
        if somme_ligne(matrice[k]) != constante_magique:
            return False
    for k in range(n):
        if somme_colonne(matrice, k) != constante_magique:
            return False
    if somme_diagonale_NO_SE(matrice) != constante_magique:
        return False
    if somme_diagonale_SO_NE(matrice) != constante_magique:
        return False
    return True