TP - Utiliser une interface d'arbre binaire

Dans le dossier [NSI], créez le dossier [A04-Arbres].

Téléchargez le module TAD_ArbresBin.py (clic droit -> [Enregistrer la cible du lien sous]) qui contient une implémentation d'arbre binaire et placez ce module dans votre répertoire de travail.

L'interface est celle donnée dans le cours :

Méthode/Opérations	Description
A = ArbreBin(rac, fg, fd)	Initialisation d'un arbre binaire de racine rac, de fils gauche et fils droit les arbres fg et fd Ces trois paramètres sont initialisés à None par défaut
est_vide(A)	Renvoie True si l'arbre est vide, False sinon.
racine(A)	Renvoie la valeur de la racine de l’arbre A si cette racine existe, None sinon.
fils_gauche(A)	Renvoie le sous-arbre (fils) gauche de A si ce sous-arbre existe, un arbre vide sinon.
fils_droit(A)	Renvoie le sous-arbre (fils) gauche de A si ce sous-arbre existe, un arbre vide sinon.

Attention

Cette interface n'est pas orientée objet, elle s'utilise de la même manière que dans les exemples du cours et dans le TD.

Affichage

Pour visualiser cet arbre, vous avez deux possibilités :

• La fonction print() réalise un affichage en ligne de l'arbre A passé en argument.
• La fonction affiche_arbreBin() réalise un affichage en deux dimensions de l'arbre A passé en argument. Cet affichage est effectué à l'aide du module turtle (merci à Q. CHAMUSSY, enseignant dans l'académie de Lyon, pour l'idée originale de cette fonction).

Ce TP a pour but de vous faire définir des fonctions (opérations) récursives et usuelles sur la structure de données « arbre binaire ».

Téléchargez le fichier « à trous » TPA04.10.py (clic droit -> [Enregistrer la cible du lien sous]) et enregistrez-le dans le dossier [A04-Arbres].

Important

L'utilisation des fonctions min() et max() pré-programmées de Python est autorisée.

Partie A - Préparer les arbres de test

Afin de tester chacune des fonctions à programmer dans ce TP et vous familiariser avec l'interface, programmez les deux arbres ci-dessous dans le « main » de votre programme.
Affichez chaque arbre afin de vérifier votre travail.

Arbre n°1

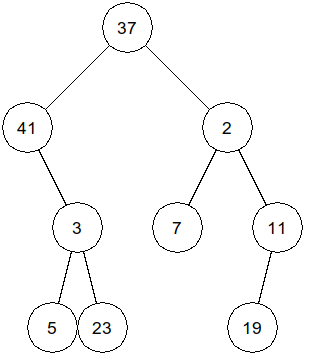
Arbre n°2

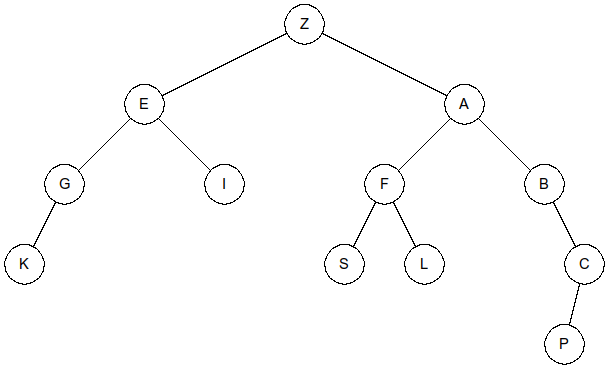
Partie B - Nombre de nœuds

Complétez la définition récursive de la fonction taille() qui prend en paramètre un arbre binaire et qui renvoie le nombre de nœuds de cet arbre.

def taille(arbre):
    """
    arbre - ArbreBin
    Sortie: int, nombre de noeuds de arbre
    """

Plan de test

>>> taille(arbre1)
9

>>> taille(arbre2)
12

Partie C - Hauteur

Complétez la définition récursive de la fonction hauteur() qui prend en paramètre un arbre binaire et qui renvoie la hauteur de cet arbre.

Rappel - Convention

Pour définir la hauteur d'un arbre, nous prenons la convention suivante :

• La hauteur de l’arbre vide est 0 ;
• La hauteur de l’arbre réduit à sa racine est 1 ;
• La hauteur d’un arbre quelconque est la plus grande valeur parmi les profondeurs des nœuds de cet arbre.

def hauteur(arbre):
    """
    arbre - ArbreBin
    Sortie: int, hauteur de arbre (l'arbre vide a pour hauteur 0)
    """

Plan de test

>>> hauteur(arbre1)
4

>>> hauteur(arbre2)
5

Partie D - Somme des nœuds

Complétez la définition récursive de la fonction sommeNoeuds() qui prend en paramètre un arbre binaire dont les nœuds sont des entiers et qui renvoie la somme des noeuds de cet arbre.

def sommeNoeuds(arbre):
    """
    arbre - ArbreBin dont les nœuds sont des entiers
    Sortie: int - Somme des noeuds de arbre
    """

Plan de test

>>> sommeNoeuds(arbre1)
148

Partie E - Plus grand nœud

Complétez la définition récursive de la fonction valeurMaxNoeud() qui prend en paramètre un arbre non vide d'éléments comparables et qui renvoie le plus grand des nœuds de cet arbre.

def valeurMaxNoeud(arbre):
    """
    arbre - ArbreBin non vide d'éléments comparables
    Sortie: Plus grand des nœuds de arbre
    """

Plan de test

>>> valeurMaxNoeud(arbre1)
41

>>> valeurMaxNoeud(arbre2)
'Z'

>>> valeurMaxNoeud(ArbreBin())
AssertionError: Arbre vide !

Partie F - Appartenance

Complétez la définition récursive de la fonction estPresent() qui prend en paramètres un arbre et une valeur de même type que les noeuds de cet arbre et qui renvoie True si cet élément fait partie des nœuds de l'arbre.

def estPresent(arbre, valeur):
    """
    arbre - ArbreBin d'éléments comparables
    valeur - Une valeur de même type que les nœuds de arbre
    Sortie: bool - True si valeur est un nœud de arbre, False sinon
    """

Plan de test

>>> estPresent(arbre1, 7)
True

>>> estPresent(arbre1, 17)
False

>>> estPresent(arbre2, 'D')
False

>>> estPresent(arbre2,'A')
True

Partie G - Profondeur d'un noeud

Complétez la définition récursive de la fonction profondeur() qui prend en paramètre un arbre binaire et une valeur de nœud et qui renvoie la profondeur de ce nœud dans l'arbre s'il est présent, -1 sinon.

def profondeur(arbre, valeur):
    """
    arbre - ArbreBin d'éléments comparables tous distincts
    valeur - Une valeur de même type que les nœuds de arbre
    Sortie: int - profondeur de valeur si elle est dans l'arbre sous forme de nœud,
            -1 False sinon
    """

Plan de test

>>> profondeur(arbre1, 7)
3

>>> profondeur(arbre1, 17)
-1

>>> profondeur(arbre2, 'A')
2