Les Arbres☘

Un arbre est un type abstrait de données contenant des éléments, appelés nœuds, accessibles de manière hiérarchique. Chaque nœud, hormis un, possède un père (un prédécesseur) et un seul. La racine est l’unique nœud qui n’a pas de père.

On peut utiliser des arbres pour schématiser de nombreuses situations.

Exemples

Arborescence des fichiers du système d’exploitation Linux ;
Arbre généalogique ;
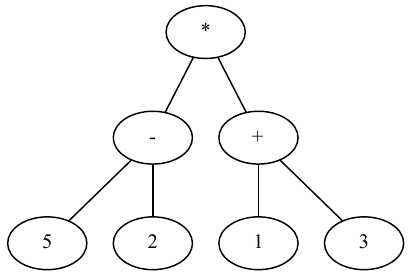
Expression arithmétique ;
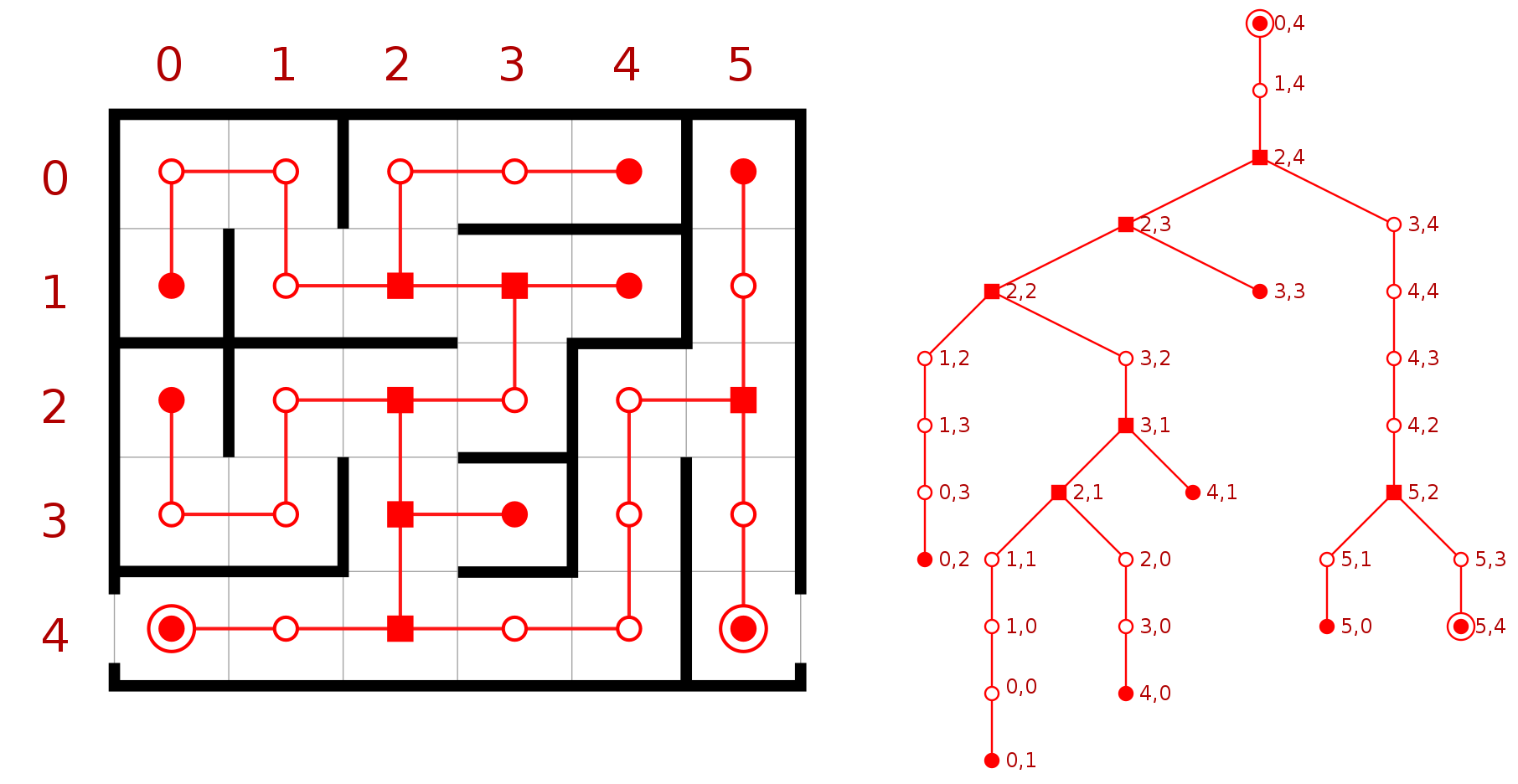
Représentation d’un labyrinthe (source wikipédia).

Arbre binaire☘

Un arbre binaire est un arbre pour lequel chaque nœud a au plus deux fils, usuellement nommés « fils gauche » et « fils droit ».

Définition récursive☘

Un arbre binaire est :

soit vide ;
soit sous la forme d'un triplet constitué d'un nœud (la racine), et de deux sous-arbres binaires (sous-arbres gauche et droit).

Interface d’un arbre binaire☘

Il existe de nombreuses possibilités d’interfaces (et d’implémentations) pour une structure d’arbre binaire. En voici une :

Méthode/Opérations	Description
`A = Arbre(rac, fg, fd)`	Initialisation d'un arbre binaire de racine `rac`, de fils gauche et fils droit les arbres `fg` et `fd`
`est_vide(A)`	Renvoie `True` si l'arbre est vide, `False` sinon.
`racine(A)`	Renvoie la valeur de la racine de l’arbre `A` si cette racine existe, `None` sinon.
`fils_gauche(A)`	Renvoie le sous-arbre (fils) gauche de `A` si ce sous-arbre existe, un arbre vide sinon.
`fils_droit(A)`	Renvoie le sous-arbre (fils) droit de `A` si ce sous-arbre existe, un arbre vide sinon.