Aller au contenu

Exercices pour s'entraîner☘

Prenez l'habitude de revenir vous entraîner régulièrement avec ces exercices tout au long de l'année. Ils sont généralement accompagnés de pistes et de leur solution pour vous permettre de progresser.

Rappels

  • Chaque programme Python doit être sauvegardé sous forme de fichier texte avec l'extension .py.
    Enregistrez ce fichier dans le dossier [A04-Arbres] avec le nom donné à l'exercice : ProgA04.51.py, ProgA04.52.py, etc...
  • Pour exécuter ce programme, il suffit de le sauvegarder puis d'appuyer sur la touche [F5].

Préambule☘

Téléchargez le module TAD_ArbresBin.py qui contient une implémentation d'arbre binaire et placez ce module dans votre répertoire de travail.

L'interface est celle donnée dans le cours :

Méthode/Opérations Description
A = ArbreBin(rac, fg, fd) Initialisation d'un arbre binaire de racine rac, de fils gauche et fils droit les arbres fg et fd
Ces trois paramètres sont initialisés à None par défaut
est_vide(A) Renvoie True si l'arbre est vide, False sinon.
racine(A) Renvoie la valeur de la racine de l’arbre A si cette racine existe, None sinon.
fils_gauche(A) Renvoie le sous-arbre (fils) gauche de A si ce sous-arbre existe, un arbre vide sinon.
fils_droit(A) Renvoie le sous-arbre (fils) gauche de A si ce sous-arbre existe, un arbre vide sinon.

Attention

Cette interface n'est pas orientée objet, elle s'utilise de la même manière que dans les exemples du cours et dans le TD.

Affichage

Pour visualiser cet arbre, vous avez deux possibilités :

  • La fonction print() réalise un affichage en ligne de l'arbre A passé en argument.
  • La fonction affiche_arbreBin() réalise un affichage en deux dimensions de l'arbre A passé en argument. Cet affichage est effectué à l'aide du module turtle (merci à Q. CHAMUSSY, enseignant dans l'académie de Lyon, pour l'idée originale de cette fonction).

ProgA04.51 - Automatiser l'implémentation de l'arbre☘

Il est parfois laborieux d'écrire toutes les instructions nécessaires à la mémorisation d'un arbre binaire avec l'interface proposée. Le but de cet exercice est donc d'automatiser le processus en utilisant un dictionnaire pour décrire l'arbre binaire.

Exemple

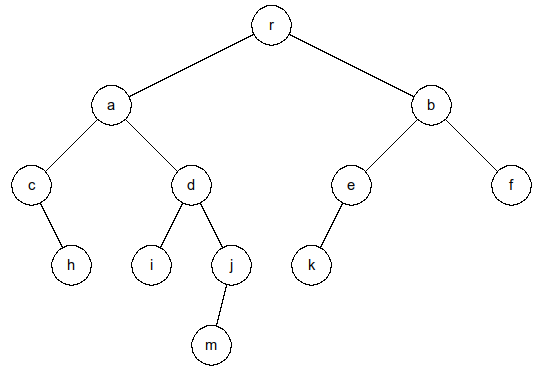arbre Voici comment décrire l'arbre dessiné ci-contre à l'aide d'un dictionnaire : 

arbre3 = {  'r' : ('a', 'b'),
            'a' : ('c', 'd'),
            'c' : (None, 'h'),
            'h' : (None, None),
            'd' : ('i', 'j'),
            'i' : (None, None),
            'j' : ('m', None),
            'm' : (None, None),
            'b' : ('e', 'f'),
            'e' : ('k', None),
            'k' : (None, None),
            'f' : (None, None)
            }

Chaque clef du dictionnaire est l'étiquette d'un noeud de l'arbre binaire.
Chaque valeur de clef est constitué d'un couple (fils gauche ; fils droit) dont chaque élément est soit None, soit la clef suivante.

Inconvénient

Avec cette représentation, les noeuds doivent tous avoir des valeurs distinctes puisqu'ils sont des clefs du dictionnaire...

  1. Complétez la définition récursive de la fonction dict_to_arbre() qui prend en paramètres un dictionnaire (dont la structure a été donnée ci-dessus) ainsi que la valeur de la racine et qui renvoie un arbre de type ArbreBin.

    1
2
3
4
5
6
    def dict_to_arbre(dico, racine):
    """
    dico - dict, dictionnaire structuré par {clef : (fg, fd)}
    racine - valeur de a première clef à prendre en compte
    Sortie: ArbreBin - Arbre binaire généré par le dictionnaire
    """

    Exemple

    >>> arbre3 = dict_to_arbre(arbre3, 'r')

>>> affiche_arbreBin(arbre3)
    arbre

    Une solution
     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
    def dict_to_arbre(dico, racine):
    """
    dico - dict, dictionnaire structuré par {clef : (fg, fd)}
    racine - valeur de a première clef à prendre en compte
    Sortie: ArbreBin - Arbre binaire généré par le dictionnaire
    """
    if racine is None:
        return racine
    if racine not in dico.keys() :
        return ArbreBin(racine)
    else:
        fils_gauche = dict_to_arbre(dico, dico[racine][0])
        fils_droit = dict_to_arbre(dico, dico[racine][1])
        return ArbreBin(racine, fils_gauche, fils_droit)
    Remarque

    La solution proposée permet de se contenter d'un dictionnaire dans lequel les feuilles de l'arbre n'ont pas besoin d'être des clefs : 

    arbre3 = {  'r' : ('a', 'b'),
            'a' : ('c', 'd'),
            'c' : (None, 'h'),
            'd' : ('i', 'j'),
            'j' : ('m', None),
            'b' : ('e', 'f'),
            'e' : ('k', None)
            }

  2. Complétez la définition récursive de la fonction arbre_to_dict() qui prend en paramètres un arbre binaire et un dictionnaire initialisé à None et qui renvoie un arbre sous la forme de dictionnaire.

    1
2
3
4
5
6
    def arbre_to_dict(arbre, dico=None):
    """
    arbre - ArbreBin, arbre binaire
    dico - dict, dictionnaire qui représentera l'arbre binaire
    Sortie: dict - dictionnaire dico structuré par {clef : (fg, fd)}
    """

    Exemple

    On entre un arbre binaire de manière usuelle dans le main : 

    1
2
3
4
5
6
    a = ArbreBin(88)
b = ArbreBin(57, a)
c = ArbreBin(62)
d = ArbreBin(74)
e = ArbreBin(51, c, d)
arbre4 = ArbreBin(94, e, b)

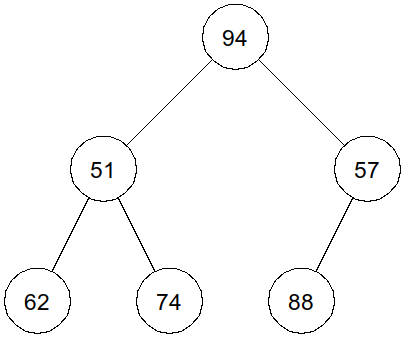
    Si on affiche l'arbre, on obtient : arbre

    Puis on exécute les instructions suivantes dans la console : 

    >>> arbre4 = arbre_to_dict(arbre4)

>>> for clef in arbre4.keys():
    ... print(f"{clef} : {arbre4[clef]}")
    ...
94 : (51, 57)
51 : (62, 74)
62 : (None, None)
74 : (None, None)
57 : (88, None)
88 : (None, None)

    Une piste

    La variable dico ayant pour valeur par défaut None, il faut tester cette valeur puis, si c'est nécessaire, initialiser dico comme un dictionnaire vide.

    Une solution
     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
    def arbre_to_dict(arbre, dico=None):
    """
    arbre - ArbreBin, arbre binaire
    dico - dict, dictionnaire qui représentera l'arbre binaire
    Sortie: dict - dictionnaire dico structuré par {clef : (fg, fd)}
    """
    if dico is None:
        dico={}
    if not est_vide(arbre):
        dico[racine(arbre)] = (racine(fils_gauche(arbre)), racine(fils_droit(arbre)))
        arbre_to_dict(fils_gauche(arbre), dico)
        arbre_to_dict(fils_droit(arbre), dico)
    return dico

ProgA04.52 - Arbre généré aléatoirement☘

Variante du programme précédent (pour les plus « paresseux »), pourquoi ne pas générer un arbre binaire aléatoirement ?

Voici un algorithme pour des nœuds de valeur entière :

  • On génère aléatoirement la valeur entière du noeud entre deux entiers fixés à l'avance.
  • On donne la probabilité d'apparition du fils gauche qui, lui aussi, est un arbre généré aléatoirement.
  • On donne la probabilité d'apparition du fils droit qui, lui aussi, est un arbre généré aléatoirement.

Pour éviter d'avoir un arbre « sans fin » on ajoute un paramètre qui correspond à la hauteur maximale de l'arbre binaire ainsi généré.

  1. Complétez la définition récursive de la fonction arbreAlea() qui permet de générer un arbre binaire aléatoire selon l'algorithme précédent et dont les nœuds sont des entiers.

    1
2
3
4
5
6
7
8
9
    def arbreAlea(hauteur, proba, b_inf, b_sup):
    """
    hauteur - int, hauteur maximale de l'arbre
    proba - float, probabilité d'apparition d'un sous-arbre (gauche ou droite)
    b_inf, b_sup - int, entiers tels que b_inf < b_sup
    Sortie: ArbreBin - Arbre binaire généré aléatoirement
            Les noeuds sont des entiers compris entre b_inf et b_sup
            hauteur est la hauteur maximale de l'arbre
    """

    Exemple

    On génère un arbre binaire de hauteur 5 (au maximum), dont les valeurs des nœuds sont des entiers compris entre 1 et 100 et de hauteur 5 au maximum : 

    >>> arbre5 = arbreAlea(5, 0.6, 1, 100)

>>> affiche_arbreBin(arbre5)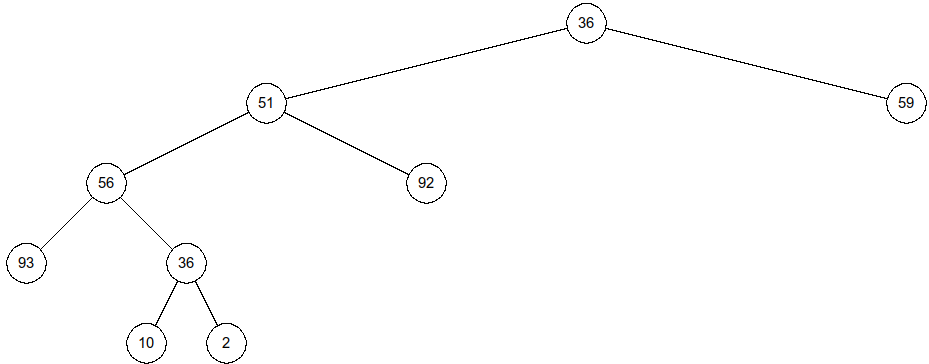
    arbre

    Une solution
     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
    def arbreAlea(hauteur, proba, b_inf, b_sup):
    """
    hauteur - int, hauteur maximale de l'arbre
    proba - float, probabilité d'apparition d'un sous-arbre (gauche ou droite)
    b_inf, b_sup - int, entiers tels que b_inf < b_sup
    Sortie: ArbreBin - Arbre binaire généré aléatoirement
            Les noeuds sont des entiers compris entre b_inf et b_sup
            hauteur est la hauteur maximale de l'arbre
    """
    if hauteur>0:
        racine = randint(b_inf, b_sup)
        fgauche, fdroit = None, None
        if random() < proba:
            fgauche = arbreAlea(hauteur-1, proba, b_inf, b_sup)
        if random() < proba:
            fdroit = arbreAlea(hauteur-1, proba, b_inf, b_sup)
        return ArbreBin(racine, fgauche, fdroit)
    else:
        return None

  2. La fonction précédente génère un arbre qui peut souvent être » déséquilibré «. Vous pouvez améliorer en diminuant la probabilité d'apparition d'une branche selon le niveau (la profondeur) à laquelle vous cherchez à générer un sous-arbre aléatoire.
    Pour ce faire, complétez la définition récursive de la fonction arbreAlea2().

    1
2
3
4
5
6
7
8
9
    def arbreAlea2(hauteur, niveau, b_inf, b_sup):
    """
    hauteur - int, hauteur maximale de l'arbre
    niveau - int, niveau de génération d'un sous-arbre (gauche ou droite)
    b_inf, b_sup - int, entiers tels que b_inf < b_sup
    Sortie: ArbreBin - Arbre binaire généré aléatoirement
            Les noeuds sont des entiers compris entre b_inf et b_sup
            hauteur est la hauteur maximale de l'arbre
    """

    Exemple

    On génère un arbre binaire de hauteur 5 (au maximum), dont les valeurs des nœuds sont des entiers compris entre 1 et 100 et de hauteur 4 au maximum : 

    >>> arbre6 = arbreAlea2(4, 0, 1, 100)

>>> affiche_arbreBin(arbre6)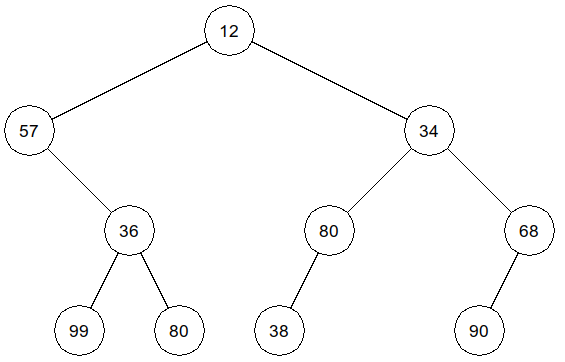
    arbre

    Une solution
     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
    def arbreAlea2(hauteur, niveau, b_inf, b_sup):
    """
    hauteur - int, hauteur maximale de l'arbre
    niveau - int, niveau de génération d'un sous-arbre (gauche ou droite)
    b_inf, b_sup - int, entiers tels que b_inf < b_sup
    Sortie: ArbreBin - Arbre binaire généré aléatoirement
            Les noeuds sont des entiers compris entre b_inf et b_sup
            hauteur est la hauteur maximale de l'arbre
    """
    if niveau<hauteur:
        racine = randint(b_inf, b_sup)
        fgauche, fdroit = None, None
        proba = (hauteur-niveau)/hauteur
        if random() < proba:
            fgauche = arbreAlea2(hauteur, niveau+1, b_inf, b_sup)
        if random() < proba:
            fdroit = arbreAlea2(hauteur, niveau+1, b_inf, b_sup)
        return ArbreBin(racine, fgauche, fdroit)
    else:
        return None

ProgA04.53 - Feuilles d'un arbre☘

Programmez la définition récursive de la fonction feuilles() qui prend en paramètre un arbre binaire et qui renvoie un tableau contenant les valeurs des feuilles de cet arbre.

1
2
3
4
5
def feuilles(lst) :
    """
    lst – Liste non vide d'éléments
    Sortie: dernier élément de la liste lst
    """

Exemples

Pour l'arbre vide : 

>>> arbre = ArbreBin()

>>> feuilles(arbre)
[]
arbre

Pour l'arbre ci-contre : 

1
2
3
4
5
6
a = ArbreBin(88)
b = ArbreBin(57, a)
c = ArbreBin(62)
d = ArbreBin(74)
e = ArbreBin(51, c, d)
arbre4 = ArbreBin(94, e, b)
On obtient : 
>>> feuilles(arbre4)
[62, 74, 88]

Une solution
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
def feuilles(arbre):
    """
    arbre - ArbreBin
    Sortie: list, tableau contenant les feuilles de arbre
    """
    if est_vide(arbre) :
        return []
    elif est_vide(fils_gauche(arbre)) and est_vide(fils_droit(arbre)):
        return [racine(arbre)]
    else:
        return feuilles(fils_gauche(arbre)) + feuilles(fils_droit(arbre))

ProgA04.54 - Plus lourde branche☘

Programmez la définition récursive de la fonction valeurMaxBranche() qui prend en paramètre un arbre binaire dont les noeuds sont des nombres (entiers ou flottants) et qui renvoie la valeur (somme des nœuds de la racine à une feuille) de la plus grande branche.

1
2
3
4
5
def valeurMaxBranche(arbre):
    """
    arbre - ArbreBin dont les noeuds sont des nombres (int ou float)
    Sortie: int ou float, somme de la plus grande branche (racine -> feuille)
    """

Exemples

Pour l'arbre vide : 

>>> arbre = ArbreBin()

>>> valeurMaxBranche(arbre)
0

arbre Pour l'arbre ci-contre : 

1
2
3
4
5
6
a = ArbreBin(88)
b = ArbreBin(57, a)
c = ArbreBin(62)
d = ArbreBin(74)
e = ArbreBin(51, c, d)
arbre4 = ArbreBin(94, e, b)
On obtient : 
>>> valeurMaxBranche(arbre4)
239

Une solution
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
def insere_fin(elt, lst):
    """
    elt – une valeur de même type que les éléments de lst
    lst – Liste non vide d'éléments
    Sortie: Liste - lst dans laquelle elt est insérée en dernier
    """
    if est_vide(lst):
        return insererEnTete(elt, lst)
    else:
        debut = tete(lst)
        fin = queue(lst)
        return insererEnTete(debut, insere_fin(elt, fin))

ProgA04.55 - Nature des arbres☘

  1. Un arbre est dit dégénéré lorsque tous ses « noeuds pères » n'ont qu'un seul enfant.
    Programmez la définition récursive de la fonction estDegenere() qui prend en paramètre un arbre binaire et qui renvoie True si cet arbre est dégénéré, False sinon.

    1
2
3
4
5
6
    def estDegenere(arbre):
    """
    arbre - ArbreBin
    Sortie: bool - True si tous les nœuds internes n’ont qu’un seul enfant,
                    False sinon
    """

    Exemples

    arbre Pour l'arbre ci-contre : 

    1
2
3
4
5
6
    a = ArbreBin(88)
b = ArbreBin(57, a)
c = ArbreBin(62)
d = ArbreBin(74)
e = ArbreBin(51, c, d)
arbre4 = ArbreBin(94, e, b)
    On obtient : 
    >>> estDegenere(arbre4)
False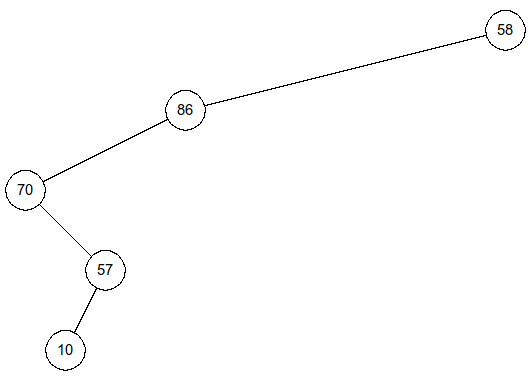

    arbre Pour l'arbre ci-contre : 

    1
2
3
4
5
    a = ArbreBin(10)
b = ArbreBin(57, a)
c = ArbreBin(70, None, b)
d = ArbreBin(86, c)
arbre7 = ArbreBin(58, d)
    On obtient : 
    >>> estDegenere(arbre7)
True

    Une solution
     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
    def estDegenere(arbre):
    """
    arbre - ArbreBin
    Sortie: bool - True si tous les nœuds internes n’ont qu’un seul enfant,
                    False sinon
    """
    if est_vide(arbre):
        return True
    elif est_vide(fils_gauche(arbre)) and not est_vide(fils_droit(arbre)):
        return estDegenere(fils_droit(arbre))
    elif est_vide(fils_droit(arbre)) and not est_vide(fils_gauche(arbre)):
        return estDegenere(fils_gauche(arbre))
    else:
        return False

  2. Un arbre est dit strict lorsque tous ses « noeuds pères » possèdent un nombre pair d'enfants (0 ou 2).
    Programmez la définition récursive de la fonction estStrict() qui prend en paramètre un arbre binaire et qui renvoie True si cet arbre est strict, False sinon.

    1
2
3
4
5
6
    def estStrict(arbre):
    """
    arbre - ArbreBin
    Sortie: bool - True si chaque "noeud-père" possède un nombre pair d’enfants
                   (0 ou 2), False sinon
    """

    Exemples

    arbre Pour l'arbre ci-contre : 

    1
2
3
4
5
6
    a = ArbreBin(88)
b = ArbreBin(57, a)
c = ArbreBin(62)
d = ArbreBin(74)
e = ArbreBin(51, c, d)
arbre4 = ArbreBin(94, e, b)
    On obtient : 
    >>> estStrict(arbre4)
False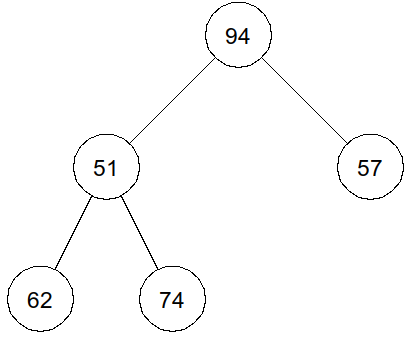

    arbre Pour l'arbre ci-contre : 

    1
2
3
4
5
    b = ArbreBin(57)
c = ArbreBin(62)
d = ArbreBin(74)
e = ArbreBin(51, c, d)
arbre8 = ArbreBin(94, e, b)
    On obtient : 
    >>> estStrict(arbre8)
True

    Une solution
     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
    def estStrict(arbre):
    """
    arbre - ArbreBin
    Sortie: bool - True si chaque "noeud-père" possède un nombre pair d’enfants
                   (0 ou 2), False sinon
    """
    if est_vide(arbre):
        return True
    elif not est_vide(fils_gauche(arbre)) and not est_vide(fils_droit(arbre)):
        return estStrict(fils_gauche(arbre)) and estStrict(fils_droit(arbre))
    else:
        return False

ProgA04.56 - Arbres égaux☘

Programmez la définition récursive de la fonction sontEgaux() qui prend en paramètre deux arbres binaires et qui renvoie True si ces arbres sont identiques (mêmes sous-arbres gauches et mêmes sous-arbres droits).

1
2
3
4
5
def sontEgaux(arbre1, arbre2):
    """
    arbre1, arbre2 - ArbreBin
    Sortie: bool - True si les deux arbres sont identiques, False sinon
    """

Exemples

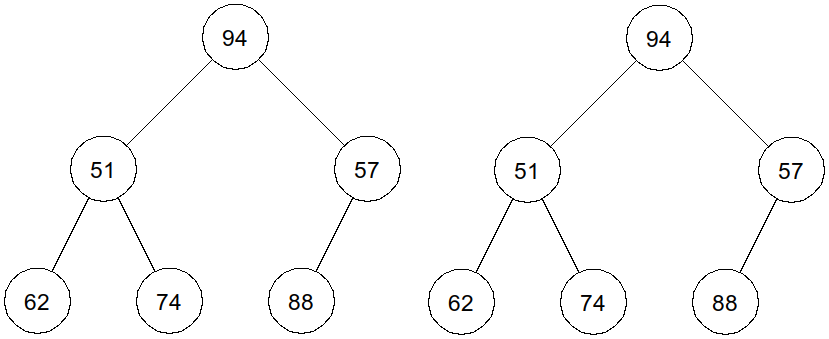
Les arbres ci-dessous sont égaux : arbre

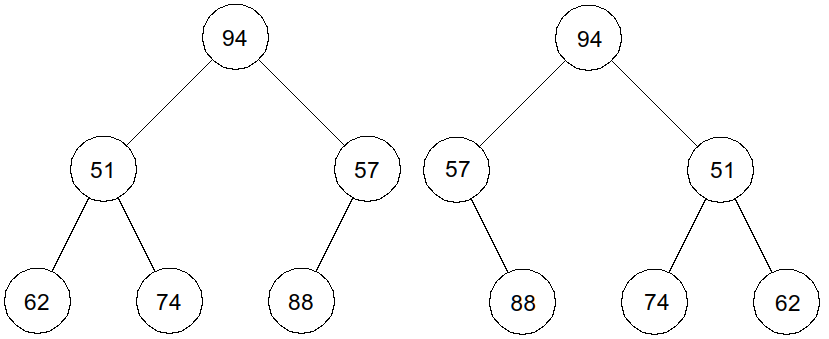
Les arbres ci-dessous ne le sont pas : arbre

Une solution
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
def sontEgaux(arbre1, arbre2):
    """
    arbre1, arbre2 - ArbreBin
    Sortie: bool - True si les deux arbres sont identiques, False sinon
    """
    if est_vide(arbre1) and est_vide(arbre2):
        return True
    elif est_vide(arbre1) and not est_vide(arbre2):
        return False
    elif est_vide(arbre2) and not est_vide(arbre1):
        return False
    else:
        return sontEgaux(fils_gauche(arbre1), fils_gauche(arbre2)) and sontEgaux(fils_droit(arbre1), fils_droit(arbre2))