TP - Algorithmes de tri

Dans le dossier [NSI], commencez par créer le dossier [E01-Diviser_Regner].

Ce TP est partagé en deux parties :

1. Dans la première partie, il est demandé d'implémenter l'algorithme de tri fusion de manière récursive (comme étudié en classe) puis impérative.

2. Dans la seconde partie, il faut implémenter d'autres algorithmes de tri puis comparer graphiquement l'efficacité de ces algorithmes à l'aide d'une fonction fournie.

TPE01.11 - Tri Fusion

Téléchargez le fichier « à trous » TPE01.11.py (clic droit -> [Enregistrer la cible du lien sous]) et enregistrez-le dans le dossier [E01-Diviser_Regner].

1. Si vous ne l'avez pas encore programmée en exercice, complétez la définition de la fonction tranche() qui renvoie un tableau contenant les éléments situés entre les indices i (inclus) et j (exclus) du tableau tab passé en paramètre.

   def tranche(tab, i, j):
       """
       tab – list, un tableau
       i, j - int, entiers positifs tels que 0 <= i <= j <= len(tab)
       Sortie: list – tableau contenant les éléments de tab situés entre les
                      indices i (inclus) et j (exclus)
       >>> tranche([1, 2, 4, 8, 16, 32], 2, 5)
       [4, 8, 16]
       >>> tranche([1, 2, 4, 8, 16, 32], 4, 6)
       [16, 32]
       >>> tranche([1, 2, 4, 8, 16, 32], 4, 4)
       []
       >>> tranche([1, 2, 4, 8, 16, 32], 4, 5)
       [16]
       """
   

   Utilisez une assertion sur les valeurs des paramètres i et j.

2. Complétez la définition de la fonction fusionner() qui prend en paramètre deux tableaux dont les éléments sont triés par ordre croissant et qui renvoie un seul tableau contenant l'ensmble des éléments (toujours triés en ordre croissant).

   def fusionner(tab1, tab2):
       """
       tab1, tab2 – list, deux tableaux d'éléments comparables et triés par ordre croissant
       Sortie: list – tableau contenant les éléments de tab1 et tab2 triés par ordre croissant
       >>> fusionner([1, 2, 8, 32], [4, 8, 16, 32])
       [1, 2, 4, 8, 8, 16, 32, 32]
       >>> fusionner([1, 2, 4], [8, 16, 32])
       [1, 2, 4, 8, 16, 32]
       """
   

3. Complétez la définition récursive de la fonction tri_fusion() qui prend en paramètre un tableau et qui renvoie un tableau contenant les mêmes éléments mais triés par ordre croissant.

   def tri_fusion(tab):
       """
       tab – list, tableau d'éléments comparables
       Sortie: list – tableau contenant les mêmes éléments mais triés par ordre croissant
       >>> tri_fusion([4, 8, 1, 32, 16, 8, 2, 32])
       [1, 2, 4, 8, 8, 16, 32, 32]
       """
   

   Dans le main, ajoutez un test de cette fonction sur un tableau d'entiers générés aléatoirement.

4. Complétez la définition impérative de la fonction tri_fusion_imp() qui prend en paramètre un tableau et qui renvoie un tableau contenant les mêmes éléments mais triés par ordre croissant.

   def tri_fusion_imp(tab):
       """
       tab – list, tableau d'éléments comparables
       Sortie: list – tableau contenant les mêmes éléments mais triés par ordre croissant
       >>> tri_fusion([4, 8, 1, 32, 16, 8, 2, 32])
       [1, 2, 4, 8, 8, 16, 32, 32]
       """
   

   Cette fonction pourra toujours faire appel à la fonction fusionner() définie à la question 2..

   Une illustration vidéo

   Un algorithme

   1. Construire un tableau dont les éléments sont des tableaux contenant chacun un seul des éléments de tab.

   2. Parcourir ce tableau par pas de 2 et placer dans un tableau temporaire la fusion des sous-tableaux deux par deux (attention, il peut y avoir un nombre impair de sous-tableaux).

   3. Recopier le contenu du tableau temporaire dans le tableau de travail.

   4. Poursuivre jusqu'à n'avoir plus qu'un sous-tableau dans le tableau de travail : ce sous tableau est trié.

TPE01.12 - Comparer des algorithmes de tri

Téléchargez le fichier « à trous » TPE01.12.py (clic droit -> [Enregistrer la cible du lien sous]) et enregistrez-le dans le dossier [E01-Diviser_Regner].

Dans ce fichier, une implémentation du tri fusion est déjà réalisée.

1. Programmez l'algorithme de tri par sélection (du maximum) en reprogrammant la définition de la fonction tri_selection() plutôt qu'en copiant un travail déjà réalisé ultérieurement.

   Rappel

   Vous pouvez aussi programmer des fonctions supplémentaires si vous en avez besoin...

2. Programmez l'algorithme de tri par insertion en reprogrammant la définition de la fonction tri_insertion() plutôt qu'en copiant un travail déjà réalisé ultérieurement.

3. Complétez la définition de la fonction tri_bulle() qui implémente le tri à bulle dont l'algorithme est détaillé ci-dessous :

   Algorithme du tri à bulles

   Le principe consiste à faire remonter progressivement les plus grands éléments à la fin du tableau :

   1. On parcourt le tableau du début à la fin en comparant les éléments deux à deux. S’ils ne sont pas dans l’ordre croissant, ils sont permutés.
   2. On recommence jusqu'à ce que plus aucune permutation ne soit possible. Le tableau est alors trié.

4. Complétez la définition récursive de la fonction tri_rapide() qui implémente le tri rapide dont l'algorithme est détaillé ci-dessous :

   Algorithme du tri rapide

   Le principe consiste à classer les éléments autour d'un pivot (les éléments de valeur plus petite sont placés à gauche, ceux de valeur plus grande sont placés à droite) :

   1. Si le tableau ne contient qu'un seul élément (ou aucun), on le renvoie.
   2. Sinon :
      1. Le pivot est le premier élément du tableau ;
      2. Un tableau « à gauche » contient tous les éléments strictement inférieurs au pivot ;
      3. Un tableau « à droite » contient tous les éléments strictement supérieurs au pivot ;
      4. On renvoie un tableau constitué du tableau gauche trié par tri rapide, du pivot puis du tableau droit trié par tri rapide.

   Attention de bien prendre en compte le cas de valeurs égales...

5. Téléchargez le fichier suivant : TPE01.12_compare.py et enregistrez-le dans votre répertoire de travail.
   Ce fichier fait appel au fichier TPE01_12.py complété dans cette partie.
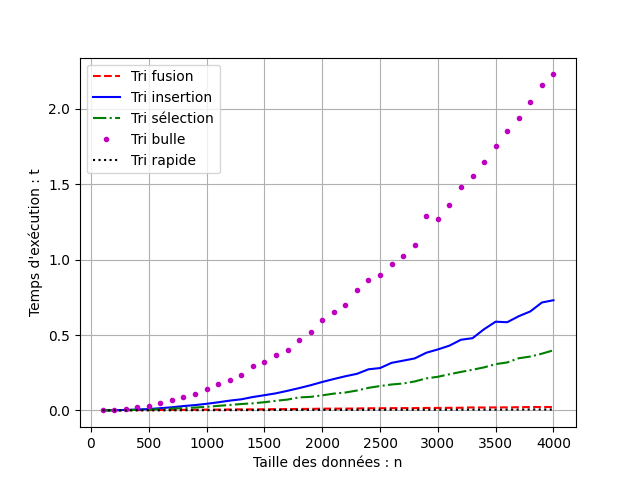
   Exécutez ce fichier afin de visualiser la complexité des tris ainsi implémentés.

   Graphique à obtenir

   Voici un exemple de graphique que l'on peut obtenir :