TP - Points les plus proches dans le plan

Ce TP a pour objectif de résoudre le problème suivant :

Des points sont placés dans un repère du plan.
Comment déterminer les coordonnées des deux points les plus proches parmi ces points ?

Pour résoudre ce problème, téléchargez puis complétez le fichier TPE01.21.py en suivant pas à pas les questions de ce TP.

Important

Dans ce TP :

• un point est assimilé à un couple de coordonnées (entières).
  Ainsi, le couple (3, 4) représente le point de coordonnées (3 ; 4).
• L'usage de la fonction min() est autorisé. Entre deux t-uplets, cette fonction renvoie le plus petit des deux selon la valeur du premier élément. En cas d'égalité, c'est la valeur du second élément qui départage.

Partie A - Travail préparatoire

1. Complétez la définition de la fonction distance() qui prend en paramètres deux points (c'est-à-dire deux couples d'entiers) et qui renvoie le flottant correspondant à la distance entre ces deux points.

   Exemple de test

   >>> distance( (-1, 3), (2, -1) )
   5.0
   

2. Complétez la définition de la fonction nuage() qui prend en paramètres trois entiers n, mini et maxi, avec mini initialisé à -20 et maxi initialisé à 20. Cette fonction renvoie un tableau de n points dont les coordonnées sont générées aléatoirement et comprises entre mini et maxi.
   Cette fonction doit vérifier l'assertion ci-dessous :

   >>> nuage(0)
   AssertionError: Le nuage doit comporter au moins deux points
   

3. Testez la fonction nuage() en effectuant un affichage des points dans le plan à l'aide de la fonction affiche_nuage() déjà programmée.

   Exemple d'utilisation de affiche_nuage()

   Puisque la fonction nuage() renvoie un ensemble de points dont les coordonnées sont générées aléatoirement, voici un exemple avec un tableau de points « statiques » :

   >>> points = [(-3, -14), (12, -11), (-19, 3), (20, -12), (-7, 6), (14, -15)]
   >>> affiche_nuage(points)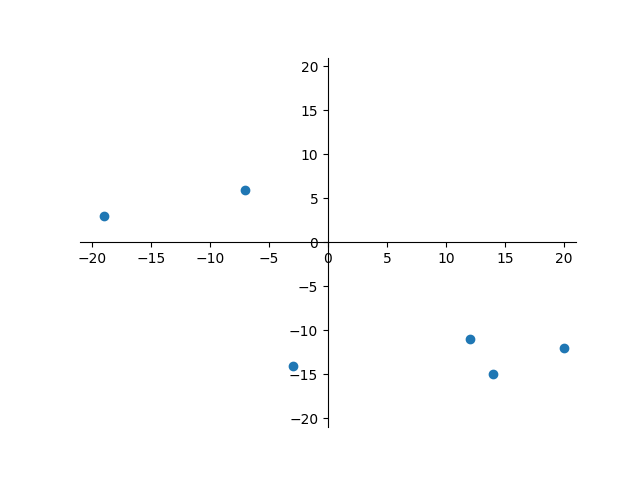
   

   

Partie B - Algorithme naïf

Cet algorithme consiste à calculer toutes les distances possibles entre deux points quelconques du nuage.

1. Complétez la définition de la fonction plus_proche_naif() qui prend en paramètres un « tableau de points » et qui renvoie un triplet constitué de la distance minimale et des deux points réalisant cette distance.

   Exemple de test

   >>> nuage_test = [(5, 6), (-1, 4), (3, -4), (-8, -7)]
   >>> plus_proche_naif( nuage_test )
   (6.324555320336759, (5, 6), (-1, 4))
   

   Conseil

   Si p1 et p2 sont deux points, alors la distance entre p1 et p2 est la même que celle entre p2 et p1. Inutile donc de calculer deux fois cette distance.

2. Vous pouvez vérifier graphiquement ce résultat en en effectuant un affichage des points dans le plan à l'aide de la fonction affiche_plus_proche() déjà programmée.

   Exemple d'utilisation de affiche_plus_proche()

   Puisque la fonction nuage() renvoie un ensemble de points dont les coordonnées sont générées aléatoirement, voici un exemple avec un tableau de points « statiques » :

   >>> points = [(-3, -14), (12, -11), (-19, 3), (20, -12), (-7, 6), (14, -15)]
   >>> d, p1, p2 = plus_proche_naif( points )
   >>> affiche_plus_proche(points, p1, p2)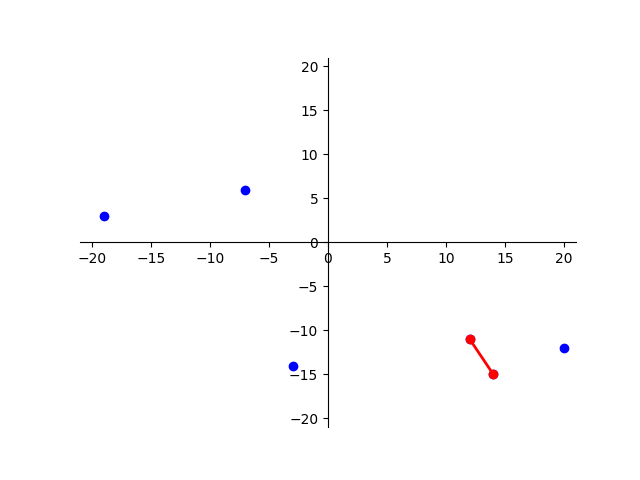
   

   

3. Déterminez la complexité de cet algorithme.
   Appelez l'enseignant pour vérifier votre raisonnement.

Partie C - Algorithme « Diviser pour Régner »

Principe

1. A partir du tableau de points, on créé deux tableaux tab_x et tab_y contenant les mêmes points. :

   1. dans le tableau tab_x, les points sont classés par ordre croissant d'abscisse ;
   2. dans le tableau tab_y, les points sont classés par ordre croissant d'ordonnée.

2. On utilise le tableau tab_x pour partager l'ensemble des points en deux ensembles de même effectif (à un près), toujours ordonnés par ordre croissant d'abscisse.

3. On poursuit récursivement jusqu'à obtenir des ensembles constitués de deux ou trois points. Dans cette situation (cas de base), on effectue un calcul à l'aide de l'algorithme naïf.

4. On obtient ainsi une distance minimale d_min dans chacun des sous-ensembles.
   Toutefois, il reste possible qu'il y ait deux points encore plus proche situé dans « l'ensemble de gauche » pour le premier et « l'ensemble de droite » pour le second.

5. Puisque les sous-ensemble sont séparés par une valeur d'abscisse connue x_m, on se concentre sur les points dont l'abscisse est comprise entre x_m - dist et x_m + dist.

6. On regroupe ces points dans un tableau extrait de tab_y.

7. Pour chaque point de ce tableau, on calcule sa distance à chacun des sept suivants.

   Pourquoi sept ?

   Demandez à l'enseignant, il vous expliquera oralement.

8. On compare la distance obtenue avec d_min et on renvoie la plus petite entre les deux.

9. C'est terminé.

Mise en œuvre

De manière à faciliter la programmation de la fonction principale, vous allez coder au fur et à mesure des fonctions nécessaires à la mise en oeuvre de l'algorithme décrit ci-dessus.
Par conséquent, les questions 1., 2. et 3. sont indépendantes. C'est à partir de la question 4. qu'il faudra regrouper les fonctions ainsi programmées.

1. Pour trier le tableau, nous allons utiliser une fonction de tri de tableau pré-programmée en Python. La fonction sorted() renvoie un nouveau tableau :

   new_tab = sorted(tab_a_trier, key=critere_de_tri)
   

   critere_de_tri est le nom d'une fonction qui prend pour paramètre un élément du tableau à trier et qui renvoie le champ selon lequel le tableau doit être trié. Complétez la définition de la fonction tab_ordonne() pour qu'elle renvoie les tableaux décrits dans l'algorithme.
   Une piste

   N'hésitez pas à vous servir de la fonction second_elt() comme critère de tri.

2. Complétez la définition de la fonction coupe() en respectant ses spécifications.
   Cette fonction est importante donc effectuez des tests supplémentaires à ceux proposés pour vérifier votre travail.

   Une piste

   La création de ces sous-tableaux est à réaliser en recherchant l'abscisse du point « milieu » du tableau tab_x.

3. Complétez la définition de la fonction recherche_vert() qui prend en paramètres un tableau de points triés par ordre croissant d'ordonnée et un flottant.
   Pour chaque point dans ce tableau, on calcule sa distance avec (au plus) les sept suivants et on renvoie la plus petite distance trouvée ainsi que les deux points pour lesquels cette distance minimale a été trouvée.

   Une piste

   Pour un tableau ayant 10 éléments, le sixième sera suivi de seulement 4 éléments. Il faut donc examiner sa distance à chacun de ces 4 éléments (et pas aux sept suivants dans ce cas).

4. Complétez la définition de la fonction plus_proche_dpr() en respectant les indications suivantes :

   1. un test d'assertion sur le nombre de points du nuage ;
   2. la création des deux tableaux de mêmes éléments mais l'un trié par ordre croissant d'abscisse et l'autre par ordre croissant d'ordonnée ;
   3. un appel à la fonction récursive plus_proche_rec().

5. Complétez la définition de la fonction plus_proche_rec() en vous aidant des indications données sous la forme de commentaires.

   Une piste

   Voici quelques accompagnements pour mieux comprendre ces commentaires.

   1. Le cas de base correspond au point n°3 de l'algorithme.
   2. Les sous-tableaux sont au nombre de quatre...
   3. Appels récursifs à gauche et à droite. On en déduit le triplet (dist, p1, p2) pour lequel la distance est la plus petite. On l'appelle d_min (par exemple).
   4. La création de ce sous-tableau est à réaliser en recherchant l'abscisse du point « milieu » du tableau tab_x.
      On place dans ce tableau les points de tab_y définis au point n°5 de l'algorithme.
   5. On recherche la distance minimale dans la bande verticale puis on renvoie le triplet issue de la plus petite distance entre d_min et la précédente.

6. Vous pouvez vérifier graphiquement ce résultat en effectuant un affichage des points dans le plan à l'aide de la fonction affiche_plus_proche() déjà programmée.

   Exemple d'utilisation de affiche_plus_proche()

   Puisque la fonction nuage() renvoie un ensemble de points dont les coordonnées sont générées aléatoirement, voici un exemple avec un tableau de points « statiques » :

   >>> points = [(-3, -14), (12, -11), (-19, 3), (20, -12), (-7, 6), (14, -15)]
   >>> d, p1, p2 = plus_proche_dpr( points )
   >>> affiche_plus_proche(points, p1, p2)
   

   

7. Déterminez la complexité de cet algorithme. Est-ce plus efficace que l'algorithme naïf ?
   Appelez l'enseignant pour vérifier votre raisonnement.