De la base 10 vers la base 2

Comment obtenir les chiffres binaires d'un réel positif ?

Les chiffres en base 10

On considère le nombre 8643,5712.
Il faut deux algorithmes différents pour obtenir successivement les chiffres d’un nombre à virgule écrit en base 10.

Les chiffres de la partie entière

Nous avons déjà vu que les chiffres de la partie entière s'obtiennent par une succession de divisions par 10 (divisions en cascade) jusqu'à obtenir un quotient nul :

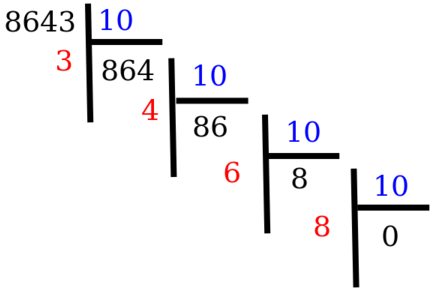
Les chiffres de la partie entière sont successivement 8, 6, 4 puis 3 (lecture à contre-sens).

Les chiffres de la partie décimale

Puisque $8643,5712 = 8 \times 10^3 + 6 \times 10^2 + 4 \times 10^1 + 3\times 10^0 + \frac{5}{10} + \frac{7}{10^2} + \frac{1}{10^3} + \frac{2}{10^4}$, les chiffres de la partie décimale s'obtiennent par une succession de multiplications par 10 :

• on isole la partie entière à chaque étape (c'est le chiffre suivant) ;
• et on multiplie par $10$ la partie décimale (nombre de la forme $0,...$).

Lorsque le « reste décimal » vaut 0, on s'arrête.

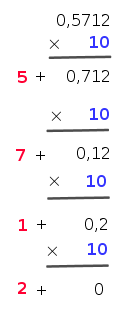
La même succession de multiplications, en ligne :

• 0,5712 × 10 = 5 + 0,712
• 0,712 × 10 = 7 + 0,12
• 0,12 × 10 = 1 + 0,2
• 0,2 × 10 = 2 + 0,0

Les chiffres de la partie décimale sont successivement 5, 7, 1 puis 2.

Conséquence

Les chiffres de la partie entière sont obtenus « à contre-sens » de l'obtention des quotients lors des divisions successives.
Les chiffres de la partie décimale sont obtenus dans l'ordre de l'obtention des parties entières lors des multiplications succesives.

Nombre réel de la base 10 vers la base 2

On procède selon le même algorithme :

Algorithme

Soit $x$ un réel positif écrit en base 10.

• Les chiffres binaires de la partie entière de $x$ s'obtiennent par des divisions successives (divisions en cascade) par 2.
• Les chiffres binaires de la partie décimale s'obtiennent par des multiplications successives par 2.

Exemple

Pour obtenir l'écriture binaire de $(3,25)_{10}$ :

• On écrit d'abord la partie entière $3$ en binaire comme on a déjà appris à le faire : $3 = (11)_2$.
• On écrit ensuite $0,25$ en binaire à l'aide de multiplications successives par 2 :
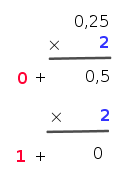  On a donc $0,25 = (0,01)_2$.

En conclusion $(3,25)_{10} = (11,01)_2$.

Exercice

Déterminer l'écriture binaire de $(5,625)_{10}$

Une solution

• On écrit d'abord la partie entière $5$ en binaire : $5 = (101)_2$.
• On écrit ensuite la partie décimale en binaire :
  • 0,625 × 2 = 1,25 = 1 + 0,25
  • 0,25 × 2 = 0,5 = 0 + 0,5
  • 0,5 × 2 = 1 = 1 + 0
    On a donc $0,625 = (0,101)_2$.

En conclusion $(5,625)_{10} = (101,101)_2$.

Un convertisseur en ligne

Vous pouvez créer vous-même d'autres exemples pour vous entraîner et vérifier vos calculs avec un convertisseur.
Par exemple, ce convertisseur en ligne.