Aller au contenu

Exercices pour s'entraîner☘

Les exercices ci-dessous ont pour but de vous familiariser avec la programmation orientée objet.

Prenez l'habitude de revenir vous entraîner régulièrement avec ces exercices tout au long de l'année. Ils sont généralement accompagnés de pistes et de leur solution pour vous permettre de progresser.

Avant de vous précipiter sur ces solutions dès la première difficulté, n'oubliez pas les conseils suivants :

  • Avez-vous bien fait un schéma au brouillon pour visualiser le problème posé ?
  • Avez-vous essayé de rédiger un algorithme en français, avec vos propres mots, avant de vous lancer dans la programmation sur machine ?
  • Avez-vous utilisé des affichages intermédiaires, des print(), pour visualiser au fur et à mesure le contenu des variables ?
  • Avez-vous testé le programme avec les propositions de tests données dans l'exercice ?
  • Avez-vous testé le programme avec de nouveaux tests, différents de ceux proposés ?

Rappels

  • Chaque programme Python doit être sauvegardé sous forme de fichier texte avec l'extension .py.
    Enregistrez ce fichier dans le dossier [D01-POO] avec le nom donné à l'exercice : ProgD01.61.py, ProgD01.62.py, etc...
  • Pour exécuter ce programme, il suffit de le sauvegarder puis d'appuyer sur la touche [F5].

ProgD01.61☘

Programmez et testez la classe Intervalle étudiée en travaux dirigés.

Attention, dans le cas de l'union, assurez-vous que [10 ; 20] \cup [12 ;8] correspond à l'intervalle [10 ; 20].

Une piste - un code à compléter
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
class Intervalle:
    """
    Une classe (structure de données) pour représenter
    un intervalle au sens mathématique du terme
    """

    def __init__(self, a, b) :
        pass


    def est_vide(self):
        pass


    def __repr__(self):
        pass


    def amplitude(self):
        pass


    def __contains__(self, valeur) :
        """
        self – Intervalle
        valeur – int ou float
        Sortie: bool - True si valeur appartient à self,
                False sinon
        """
        pass


    def __eq__(self, autreIntervalle) :
        """
        self, autreIntervalle – Intervalles
        Sortie: bool - True si les intervalles sont égaux,
                False sinon
        """
        pass


    def __le__(self, autreIntervalle) :
        """
        self, autreIntervalle – Intervalles
        Sortie: bool - True si le premier intervalle est contenu dans le second,
                False sinon
        """
        pass


    def intersection(self, autreIntervalle) :
        """
        self, autreIntervalle – Intervalles
        Sortie: Intervalle - Intervalle d'intersection entre les deux précédents.
        """
        pass


    def union(self, autreIntervalle) :
        """
        self, autreIntervalle – Intervalles
        Sortie: Intervalle - Intervalle d'union entre les deux précédents lorsque
                les deux intervalles ont une intersection non vide.
        """
        pass
Solution
  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
class Intervalle:
    """
    Une classe (structure de données) pour représenter
    un intervalle au sens mathématique du terme
    """


    def __init__(self, a, b) :
        assert isinstance(a, int) or isinstance(a, float), "Les paramètres doivent être des nombres, int ou float."
        assert isinstance(b, int) or isinstance(b, float), "Les paramètres doivent être des nombres, int ou float."
        self.borne_inf = a
        self.borne_sup = b


    def est_vide(self):
        return self.borne_sup < self.borne_inf


    def __repr__(self):
        if self.est_vide():
            return "{}"
        elif self.borne_inf == self.borne_sup:
            return "{" + str(self.borne_inf) + "}"
        else:
            return f"[{self.borne_inf} ; {self.borne_sup}]"


    def amplitude(self):
        if self.est_vide():
            return 0
        else:
            return self.borne_sup - self.borne_inf


    def __contains__(self, valeur) :
        """
        self – Intervalle
        valeur – int ou float
        Sortie: bool - True si valeur appartient à self,
                False sinon
        """
        return self.borne_inf <= valeur <= self.borne_sup


    def __eq__(self, autreIntervalle) :
        """
        self, autreIntervalle – Intervalles
        Sortie: bool - True si les intervalles sont égaux,
                False sinon
        """
        if self.est_vide() and autreIntervalle.est_vide() :
            return True
        elif self.borne_inf == autreIntervalle.borne_inf and self.borne_sup == autreIntervalle.borne_sup :
            return True
        else:
            return False


    def __le__(self, autreIntervalle) :
        """
        self, autreIntervalle – Intervalles
        Sortie: bool - True si le premier intervalle est contenu dans le second,
                False sinon
        """
        if self.est_vide() :
            return True
        elif self.borne_inf >= autreIntervalle.borne_inf and self.borne_sup <= autreIntervalle.borne_sup :
            return True
        else:
            return False


    def intersection(self, autreIntervalle) :
        """
        self, autreIntervalle – Intervalles
        Sortie: Intervalle - Intervalle d'intersection entre les deux précédents.
        """
        if self.est_vide() :
            return self
        elif autreIntervalle.est_vide() :
            return autreIntervalle
        else:
            a = max(self.borne_inf, autreIntervalle.borne_inf)
            b = min(self.borne_sup, autreIntervalle.borne_sup)
            return Intervalle(a, b)


    def union(self, autreIntervalle) :
        """
        self, autreIntervalle – Intervalles
        Sortie: Intervalle - Intervalle d'union entre les deux précédents lorsque
                les deux intervalles ont une intersection non vide.
        """
        if self.est_vide() :
            return autreIntervalle
        elif autreIntervalle.est_vide() :
            return self
        elif self.intersection(autreIntervalle).est_vide():
            return None
        else:
            a = min(self.borne_inf, autreIntervalle.borne_inf)
            b = max(self.borne_sup, autreIntervalle.borne_sup)
            return Intervalle(a, b)

ProgD01.62☘

Le but de cet exercice est de modéliser une classe Tableau dans lequel les indices des éléments du tableau ne commencent pas forcément à 0. Un objet de cette classe aura deux attributs :

  • un attribut premier qui est le numéro du premier indice ;
  • un attribut contenu qui est de type list contenant les éléments du tableau.

Attention

contenu est un tableau « classique », c'est-à-dire indexée à partir de 0.

  1. Recopier et compléter la définition du constructeur __init__() en respectant ses spécifications. Ce constructeur doit vérifier que les paramètres indice_min et indice_max sont bien entiers. De plus, dans le cas où indice_min est plus grand que indice_max, il faudra veiller à échanger ces deux valeurs.

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
    class Tableau:
    """
    Tableau de taille limité, ne commençant pas forcément à l'indice 0.
    """

    def __init__(self, indice_min, indice_max, v_init = None) :
        """
        self - instance de Tableau
        indice_min - int, indice du premier élément du Tableau
        indice_max - int, indice du dernier élément du Tableau
        v_init - Chaque case du tableau est initilialisée à cette valeur
        Sortie: None - Création d'un objet de type Tableau
        """
    Une solution
     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
    class Tableau:
    """
    Tableau de taille limité, ne commençant pas forcément à l'indice 0.
    """

    def __init__(self, indice_min, indice_max, v_init = None) :
        """
        self - instance de Tableau
        indice_min - int, indice du premier élément du Tableau
        indice_max - int, indice du dernier élément du Tableau
        v_init - Chaque case du tableau est initilialisée à cette valeur
        Sortie: None - Création d'un objet de type Tableau
        """
        assert isinstance(indice_min, int) and isinstance(indice_max, int), "Les deux premiers paramètres doivent être entiers"
        if indice_min > indice_max:
            indice_min, indice_max = indice_max, indice_min
        self.premier = indice_min
        taille_tab = indice_max - indice_min + 1
        self.contenu = [v_init]*taille_tab

  2. Surcharger la méthode __repr__() pour qu'elle renvoie une chaîne de caractères décrivant le contenu du tableau ainsi que la valeur du premier indice.

    Exemple de tests

    >>> t = Tableau(3, 8, 17)
>>> t
Premier indice : 3
[17, 17, 17, 17, 17, 17]
    Une solution
    22
23
        def __repr__(self):
        return f"Premier indice : {self.premier}\n{self.contenu}"

  3. Programmer le destructeur __del__().

    Exemple de tests

    >>> t = Tableau(3, 8)
>>> t
Premier indice : 3
[None, None, None, None, None, None]

>>> del(t)

>>> t
NameError: name 't' is not defined
    Une solution
    26
27
        def __del__(self):
        del(self.contenu)

  4. Surchager la méthode __len__() pour qu'elle renvoie le nombre d'éléments du tableau.

    Exemple de tests

    >>> t = Tableau(3, 8)
>>> len(t)
6

>>> t = Tableau(8, 5)
>>> len(t)
4
    Une solution
    30
31
        def __len__(self):
        return len(self.contenu)

  5. Programmer la méthode est_valide() qui renvoie True si l'indice i passé en paramètre est valide, c'est-à-dire compris entre le premier et le dernier indice du tableau. Cette fonction renvoie False sinon.
    Attention, l'indice i doit être un entier !

    Exemple de tests

    >>> t = Tableau(3, 8)
>>> t.est_valide(7)
True

>>> t.est_valide(8)
True

>>> t.est_valide(9)
False

>>> t.est_valide(2)
False
    Une solution
    34
35
36
        def est_valide(self, i):
        assert isinstance(i, int), "L'indice i doit être entier"
        return self.premier <= i < self.premier + len(self.contenu)

  6. Programmer la méthode get_element() qui renvoie la valeur de l'élément d'indice i passé en paramètre. Cette méthode doit lever une erreur d'assertion si l'indice i n'est pas valide.

    39
40
        def get_element(self, i):
        pass

    Exemple de tests

    >>> t = Tableau(3, 8, 17)
>>> t
Premier indice : 3
[17, 17, 17, 17, 17, 17]

>>> t.get_element(4)
17

>>> t.get_element(1)
    Une solution

    La partie else n'est pas obligatoire... 

    39
40
41
42
43
        def get_element(self, i):
        if self.est_valide(i):
            return self.contenu[i - self.premier]
        else:
            return None

  7. Programmer la méthode set_element() qui remplace, par le paramètre valeur, la valeur de l'élément d'indice i passé en paramètre. Cette méthode doit lever une erreur d'assertion si l'indice i n'est pas valide.

    46
47
        def setElement(self, i, valeur):
        pass

    Exemple de tests

    >>> t = Tableau(3, 8, 17)
>>> t
Premier indice : 3
[17, 17, 17, 17, 17, 17]

>>> t.set_element(4, -1)
>>> t
Premier indice : 3
[17, -1, 17, 17, 17, 17]

>>> t.set_element(11, 0)
AssertionError: L'indice i n'est pas compris entre le premier et le dernier indice du tableau
    Une solution
    46
47
48
        def set_element(self, i, valeur):
        assert self.est_valide(i), "L'indice i n'est pas compris entre le premier et le dernier indice du tableau"
        self.contenu[i - self.premier] = valeur

  8. Surcharger la méthode __repr__() pour qu'elle renvoie une chaîne de caractères décrivant les indices du tableau et son contenu comme présenté dans l'exemple suivant.

    Exemple de tests

    >>> from random import randint        
>>> t = Tableau(-2, 5)
>>> for i in range(-2, 6):
        t.set_element(i, randint(-20, 20))

>>> print(t)
-2  11
-1  17
0   -16
1   -8
2   -19
3   8
4   -19
5   -10
    Une piste

    On pourra utiliser le caractère spécial de tabulation '\t'.

    Une solution
    51
52
53
54
55
        def __str__(self):
        chaine = ""
        for i in range(self.premier, self.premier + len(self.contenu)):
            chaine += str(i) + '\t' + str(self.contenu[i]) + '\n'
        return chaine
Le programme complet
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
class Tableau:
    """
    Tableau de taille limité, ne commençant pas forcément à l'indice 0.
    """

    def __init__(self, indice_min, indice_max, v_init = None) :
        """
        self - instance de Tableau
        indice_min - int, indice du premier élément du Tableau
        indice_max - int, indice du dernier élément du Tableau
        v_init - Chaque case du tableau est initilialisée à cette valeur
        Sortie: None - Création d'un objet de type Tableau
        """
        assert isinstance(indice_min, int) and isinstance(indice_max, int), "Les deux premiers paramètres doivent être entiers"
        if indice_min > indice_max:
            indice_min, indice_max = indice_max, indice_min
        self.premier = indice_min
        taille_tab = indice_max - indice_min + 1
        self.contenu = [v_init]*taille_tab


    def __repr__(self):
        return f"Premier indice : {self.premier}\n{self.contenu}"


    def __del__(self):
        del(self.contenu)


    def __len__(self):
        return len(self.contenu)


    def est_valide(self, i):
        assert isinstance(i, int), "L'indice i doit être entier"
        return self.premier <= i < self.premier + len(self.contenu)


    def get_element(self, i):
        if self.est_valide(i):
            return self.contenu[i - self.premier]
        else:
            return None


    def set_element(self, i, valeur):
        assert self.est_valide(i), "L'indice i n'est pas compris entre le premier et le dernier indice du tableau"
        self.contenu[i - self.premier] = valeur


    def __str__(self):
        chaine = ""
        for i in range(self.premier, self.premier + len(self.contenu)):
            chaine += str(i) + '\t' + str(self.contenu[i]) + '\n'
        return chaine


if __name__ == "__main__":
    from random import randint

    t = Tableau(-2, 5)
    for i in range(-2, 6):
        t.set_element(i, randint(-20, 20))

    print(t)

ProgD01.63☘

Une résistance électrique, aussi appelée résistor, est un dipôle électrique passif qui reçoit ou qui utilise le courant électrique. L'unité de mesure de la résistance électrique est le ohm de symbole \Omega.

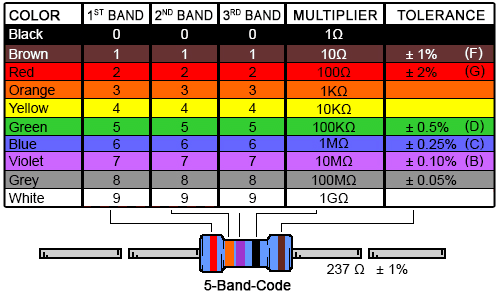
Le but de cet exercice est de modéliser par une classe les résistors à quatre bandes : resistor

Remarques

  1. Pour éviter toute confusion, le mot resistor désignera le composant physique tandis que le mot resistance désignera la grandeur de résistance, en ohms.
  2. On ne modélisera pas la tolérance (la cinquième bande) qui est spécifique au composant physique.

Définir en Python une classe Resistor dont l'attribut est resistance en respectant le cahier des charges suivant :

  1. Programmer le constructeur __init__().
    Attention, la resistance doit être un nombre entier positif. Utiliser les assertions nécessaires pour le vérifier.

    Remarque importante

    La résistance maximale sera 999 GΩ.
    Il faudra le spécifier dans le docstring mais aucun test ni aucune assertion ne seront réalisés pour le vérifier.

    Exemple de tests

    >>> r = Resistor(12.3)
AssertionError: La résistance doit être un entier positif.

>>> r = Resistor(-15)
AssertionError: La résistance doit être un entier positif.

>>> r = Resistor(15)
>>> r
<__main__.Resistor at 0x7ff65ee3d040>
    Une piste - Un code à compléter
    1
2
3
4
5
6
7
    class Resistor:
    """
    Docstring à compléter
    """

    def __init__(self, resist) :
        pass
    Une solution
     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
    class Resistor:
    """
    Une classe (structure de données) pour modéliser les résistance électriques
    comprises entre 0 Ω et 999 GΩ.
    """


    def __init__(self, resist) :
        assert isinstance(resist, int), "La résistance doit être un entier positif."
        assert resist >= 0, "La résistance doit être un entier positif."
        self.resistance = resist

  2. Programmer le destructeur __del__().

    Exemple de tests

    >>> r = Resistor(15)
>>> del(r)
<Suppression de la résistance
    Une solution
    14
15
        def __del__(self):
        print("Suppression de la résistance")

  3. Programmer la méthode get_resistance() qui renvoie la valeur de resistance du resistor.

    Exemple de tests

    >>> r = Resistor(15)
>>> r.get_resistance()
15
    Une solution
    18
19
        def get_resistance(self):
        return self.resistance

  4. Programmer la méthode approche() qui renvoie la valeur approchée (chaîne de caractères) d'une résistance sur le modèle des quatre bandes.

    Exemple de tests

    >>> r1 = Resistor(4158378)
>>> r1.approche()
'4160000'

>>> r2 = Resistor(237)
>>> r2.approche()
'237'

>>> r3 = Resistor(31625)
>>> r3.approche()
'31600'

>>> r4 = Resistor(499612)
>>> r4.approche()
'500000'
    Une piste

    La valeur de résistance peut avoir moins ou plus de chiffres. Dans ce dernier cas, la valeur du quatrième chiffre (à partir de la gauche) permet de déterminer s'il est nécessaire d'arrondir ou non.

    Transtyper la valeur d'entier à chaîne de caractères, et vice-versa, permet d'accéder plus facilement à la valeur d'un chiffre.

    Une solution
    22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
        def approche(self):
        valeur = str(self.resistance)
        if len(valeur) < 4:
            return str(self.resistance)
        else:
            # Il y a plus de 3 chiffres, on arrondit le troisième selon la valeur du quatrième
            if int(valeur[3]) < 5:
                val_approchee = valeur[0] + valeur[1] + valeur[2]
            else:
                val_approchee = str( int(valeur[0] + valeur[1] + valeur[2])+1 )

            # On complète par les zéros manquant - le nombre de chiffres de resistance moins les trois premiers
            val_approchee += "0"*(len(valeur) - 3)

            return val_approchee

  5. En faisant appel à la méthode approche(), surcharger la méthode __repr__() afin qu'elle affiche, dans l'ordre, les couleurs des quatre premières bandes du composant électrique correspondant.

    Exemple de tests

    >>> r1 = Resistor(4158378)
>>> r1
jaune marron bleu jaune

>>> r2 = Resistor(237)
>>> r2
rouge orange violet noir

>>> r3 = Resistor(31625)
>>> r3
orange marron bleu rouge

>>> r4 = Resistor(499612)
>>> r4
vert noir noir orange
    Une piste

    Vous pouvez vous servir du tableau :
    couleurs = ['noir', 'marron', 'rouge', 'orange', 'jaune', 'vert', 'bleu', 'violet', 'gris', 'blanc'].

    Une autre piste

    Séparez les résistances qui ont entre un et trois chiffres des autres...

    Une solution
    39
40
41
42
43
44
45
46
47
48
49
        def __repr__(self):
        couleurs = ['noir', 'marron', 'rouge', 'orange', 'jaune', 'vert', 'bleu', 'violet', 'gris', 'blanc']
        val = self.approche()
        if len(val) == 1:
            return f'noir noir {couleurs[int(val[0])]} noir'
        elif len(val) == 2:
            return f'noir {couleurs[int(val[0])]} {couleurs[int(val[1])]} noir'
        elif len(val) == 3:
            return f'{couleurs[int(val[0])]} {couleurs[int(val[1])]} {couleurs[int(val[2])]} noir'
        else:
            return f'{couleurs[int(val[0])]} {couleurs[int(val[1])]} {couleurs[int(val[2])]} {couleurs[len(val)-3]}'

  6. Surcharger la méthode __str__() afin qu'il renvoie la resistance approchée du resistor dans l'unité qui convient le mieux (Ω, kΩ, MΩ, GΩ).

    Exemple de tests

    >>> r1 = Resistor(4158378)
>>> print(r1)
4.16 MΩ

>>> r2 = Resistor(237)
>>> print(r2)
237 Ω

>>> r3 = Resistor(31625)
>>> print(r3)
31.6 kΩ

>>> r4 = Resistor(499612)
>>> print(r4)
500 kΩ
    Une solution
    52
53
54
55
56
57
58
59
60
61
62
63
64
65
        def __str__(self):
        unites = ['Ω', 'kΩ', 'MΩ', 'GΩ']
        val = self.approche()
        puissance = (len(val)-1)//3
        if puissance == 0:
            return f'{val} {unites[puissance]}'
        else:
            nb_chiffres = len(val) - puissance*3
            if nb_chiffres == 1:
                return f'{val[0]}.{val[1]}{val[2]} {unites[puissance]}'
            elif nb_chiffres == 2:
                return f'{val[0]}{val[1]}.{val[2]} {unites[puissance]}'
            else:
                return f'{val[0]}{val[1]}{val[2]} {unites[puissance]}'

  7. L'opérateur « - » va représenter l'association en série de deux résistors. On rappelle que la résistance équivalente R_{eq} à l'association en série de deux composants de résistances R_1 et R_2 est R_{eq} = R_1 + R_2.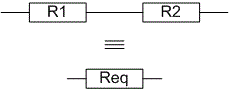 resistor Surcharger l'opérateur correspondant.

    Exemple de tests

    >>> r1 = Resistor(4158378)
>>> r2 = Resistor(237)
>>> r3 = r1-r2
>>> print(r3)
4.16 MΩ

>>> r4 = Resistor(499612)
>>> r5 = r1-r4
>>> print(r5)
4.66 MΩ
    Une solution
    68
69
        def __sub__(self, autreResistor):
        return Resistor(self.resistance + autreResistor.resistance)

  8. L'opérateur « // » va représenter l'association en parallèle de deux résistors. On rappelle que la résistance équivalente R_{eq} à l'association en parallèle de deux composants de résistances R_1 et R_2 est \frac{1}{R_{eq}} = \frac{1}{R_1} + \frac{1}{R_2}.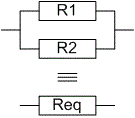 resistor Surcharger l'opérateur correspondant.

    Exemple de tests

    >>> r1 = Resistor(4158378)
>>> r2 = Resistor(237)
>>> r3 = r1//r2
>>> print(r3)
236 Ω

>>> r4 = Resistor(499612)
>>> r5 = r1//r4
>>> print(r5)
446 kΩ
    Une solution
    71
72
73
74
        def __floordiv__(self, autreResistor):
        r1 = self.resistance
        r2 = autreResistor.resistance
        return Resistor( (r1*r2) // (r1+r2) )
Le code complet
class Resistor:
    """
    Une classe (structure de données) pour modéliser les résistance électriques
    comprises entre 0 Ω et 999 GΩ.
    """


    def __init__(self, resist) :
        assert isinstance(resist, int), "La résistance doit être un entier positif."
        assert resist >= 0, "La résistance doit être un entier positif."
        self.resistance = resist


    def __del__(self):
        print("Suppression de la résistance")


    def get_resistance(self):
        return self.resistance


    def approche(self):
        valeur = str(self.resistance)
        if len(valeur) < 4:
            return str(self.resistance)
        else:
            # Il y a plus de 3 chiffres, on arrondit le troisième selon la valeur du quatrième
            if int(valeur[3]) < 5:
                val_approchee = valeur[0] + valeur[1] + valeur[2]
            else:
                val_approchee = str( int(valeur[0] + valeur[1] + valeur[2])+1 )

            # On complète par les zéros manquant - le nombre de chiffres de resistance moins les trois premiers
            val_approchee += "0"*(len(valeur) - 3)

            return val_approchee


    def __repr__(self):
        couleurs = ['noir', 'marron', 'rouge', 'orange', 'jaune', 'vert', 'bleu', 'violet', 'gris', 'blanc']
        val = self.approche()
        if len(val) == 1:
            return f'noir noir {couleurs[int(val[0])]} noir'
        elif len(val) == 2:
            return f'noir {couleurs[int(val[0])]} {couleurs[int(val[1])]} noir'
        elif len(val) == 3:
            return f'{couleurs[int(val[0])]} {couleurs[int(val[1])]} {couleurs[int(val[2])]} noir'
        else:
            return f'{couleurs[int(val[0])]} {couleurs[int(val[1])]} {couleurs[int(val[2])]} {couleurs[len(val)-3]}'


    def __str__(self):
        unites = ['Ω', 'kΩ', 'MΩ', 'GΩ']
        val = self.approche()
        puissance = (len(val)-1)//3
        if puissance == 0:
            return f'{val} {unites[puissance]}'
        else:
            nb_chiffres = len(val) - puissance*3
            if nb_chiffres == 1:
                return f'{val[0]}.{val[1]}{val[2]} {unites[puissance]}'
            elif nb_chiffres == 2:
                return f'{val[0]}{val[1]}.{val[2]} {unites[puissance]}'
            else:
                return f'{val[0]}{val[1]}{val[2]} {unites[puissance]}'


    def __sub__(self, autreResistor):
        return Resistor(self.resistance + autreResistor.resistance)

    def __floordiv__(self, autreResistor):
        r1 = self.resistance
        r2 = autreResistor.resistance
        return Resistor( (r1*r2) // (r1+r2) )