Opérations sur les listes chaînées

Initialiser une liste vide

Une liste « vide » ne pointe vers rien :

Complexité

Cette opération se réalise en temps constant, c'est-à-dire en $O(1)$.

Insérer en tête de liste chaînée

1. On crée la liste L :

2. On crée un maillon qui pointe vers le lien de L :

3. On fait pointer le lien de L vers le maillon :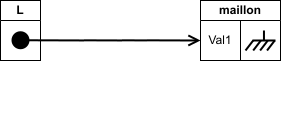

4. On recommence. On crée un maillon qui pointe vers le lien de L :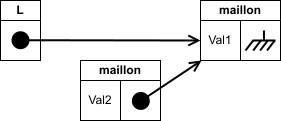

5. On fait pointer le lien de L vers le maillon :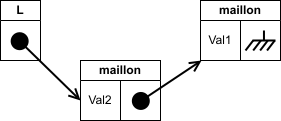

6. etc...

Complexité

Pour chaque insertion en tête de liste, la complexité en temps est constante, c'est-à-dire en $O(1)$.

Parcourir les éléments d'une liste chaînée

On considère une liste L :

Pour parcourir les éléments (maillons) de cette liste :

1. On crée une variable temp qui pointe vers le le lien de L, c'est-à-dire vers le premier maillon :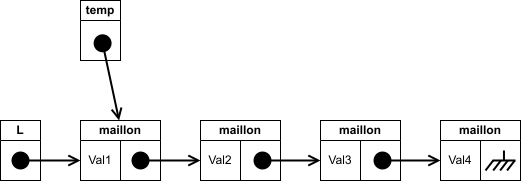

2. On utilise le lien de chaque maillon pour que temp pointe vers le maillon suivant :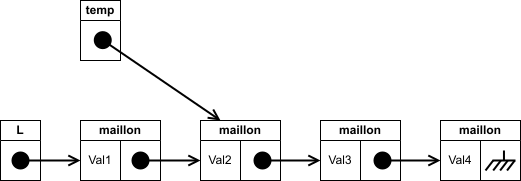

3. On s'arrête lorsque le lien du maillon pointe vers None (on est au dernier maillon) ou bien lorsqu'on est à la position désirée (on peut utiliser pour cela une variable « indice » pour chaque maillon) :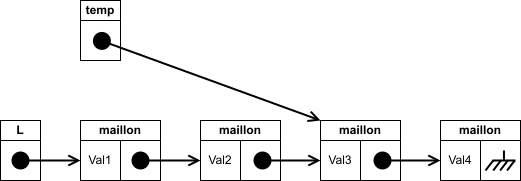

Complexité

Dans le pire des cas, il faut parcourir les $n$ maillons de la liste donc la complexité en temps est linéaire, c'est-à-dire en $O(n)$.

Insérer un élément en n'importe quelle position

1. On reprend le parcours précédent pour « s'arrêter » au maillon après lequel on souhaite insérer :

2. On crée un maillon à insérer dont le lien pointe vers le lien du maillon sur lequel on s'est arrêté :

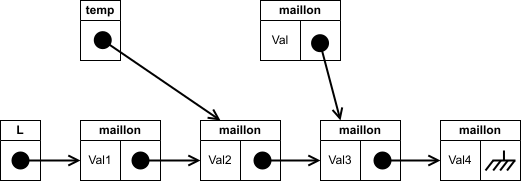
3. On redéfinit le lien du maillon sur lequel on s'est arrêté pour qu'il pointe vers le nouveau maillon :

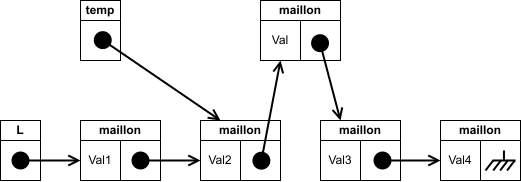
4. On obtient la liste :

Complexité

Une fois en « bonne » position, la complexité de l'insertion est constante en $O(1)$.
Par contre, pour se rendre à la bonne position, le coût est linéaire (cf. le paragraphe sur le parcours des éléments).

Supprimer un élément

1. On reprend le parcours pour se placer au maillon situé avant celui à supprimer :

2. On pointe ensuite le maillon à supprimer et on mémorise (si besoin) la valeur qu'il contient :

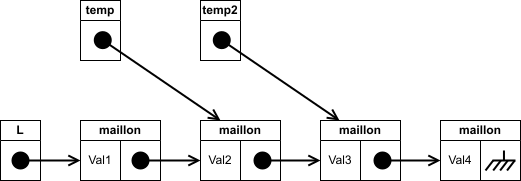
3. On redéfinit le lien du maillon sur lequel on s'est arrêté pour qu'il pointe vers le lien du maillon à supprimer :

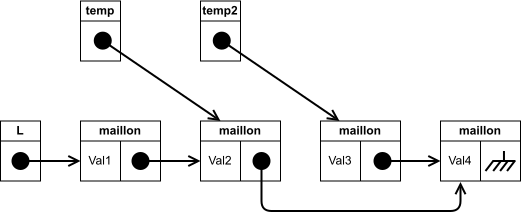
4. On obtient la liste :

Complexité

Une fois en « bonne » position, la complexité la suppression est constante en $O(1)$.
Par contre, pour se rendre à la bonne position, le coût est linéaire (cf. le paragraphe sur le parcours des éléments).