Aller au contenu

Rugby☘

Téléchargez le fichier à compléter TPG06.20.py (clic droit -> [Enregistrer sous]) et enregistrez-le dans le dossier [G06_Algo_KNN].

Consignes communes à chaque partie

Le programme principal contient un appel au module doctest : 

##----- Programme principal et tests -----##
if __name__ == '__main__':
    import doctest
    doctest.testmod()
Chacune des fonctions devra passer les tests proposés.
Il faudra aussi ajouter vos propres tests dans le « main » afin de vous entraîner à en réaliser.

Préambule - La base joueurs☘

Le site http://www.allrugby.com, permet de télécharger une base de données sur les différents joueurs du Top14. Un extrait de la base de la saison 2019-2020 est disponible dans le fichier joueurs_BDD.csv.

  1. Téléchargez et sauvegardez ce fichier dans votre répertoire de travail.

  2. En utilisant la bibliothèque fonctions_csv.py déjà utilisée dans le traitement des données, complétez la définition de la fonction importation() pour :

    1. importer la base joueurs sous la forme d'une table de dictionnaires.
    2. ne conserver que les attributs 'Nom', 'Type poste', 'Taille (en cm)'et 'Poids (en kg)'.
    3. convertir les attributs nécessaire en entiers.
    4. afficher chaque dictionnaire de cette table pour vérifier votre importation.
    Affichage à obtenir

    Voici les premières lignes de la table contenue dans la variable joueurs : 

    1
2
3
4
5
6
    {'Nom': 'Carlü SADIE', 'Type poste': 'Avant', 'Taille (en cm)': 180, 'Poids (en kg)': 124}
{'Nom': 'Fritz LEE', 'Type poste': '3ème ligne', 'Taille (en cm)': 188, 'Poids (en kg)': 107}
{'Nom': 'Kitione KAMIKAMICA', 'Type poste': '3ème ligne', 'Taille (en cm)': 188, 'Poids (en kg)': 105}
{'Nom': 'Daniel BRENNAN', 'Type poste': 'Avant', 'Taille (en cm)': 192, 'Poids (en kg)': 132}
{'Nom': 'Quentin BÉTHUNE', 'Type poste': 'Avant', 'Taille (en cm)': 183, 'Poids (en kg)': 112}
{'Nom': 'Joketani KOROI', 'Type poste': '3ème ligne', 'Taille (en cm)': 198, 'Poids (en kg)': 115}

  3. La fonction representation() a été définie dans le programme pour visualiser ces données à l'aide de la bibliothèque matplotlib.pyplot comme dans la page Représentation Graphique.
    Appliquez cette fonction à la variable joueurs et vérifiez que vous obtenez la représentation graphique suivante :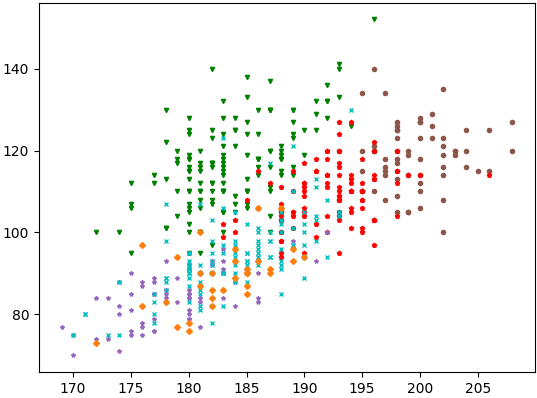 Représentation graphique de la base joueurs

Partie A - Implémenter l'algorithme k-NN☘

De la même manière que dans le TP sur les iris, complétez le code des trois fonctions distance(), k_plus_proches() et classification() en respectant les contraintes suivantes :

  • La distance choisie est celle de Manhattan ;
  • Ces trois fonctions doivent utiliser au maximum les variables globales définies au début du programme.

Conseil

Prenez le temps de bien étudier le début du programme avant de vous lancer dans la programmation.

Code des fonctions à compléter
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
def distance(donnee1, donnee2):
    """
    donnee1, donnee2 - dict, dictionnaires qui contiennent (au moins)
                       les clefs du tableau ATTRIBUTS
    Sortie: float - Distance de Manhattan entre les deux données
    """
    pass


def k_plus_proches(k, a_classer, BDD):
    """
    k - int, entier strictement positif (nombre de voisins)
    a_classer - dict, dictionnaires qui contient (au moins)
                      les clefs du tableau ATTRIBUTS
    BDD - list, Tableau de dictionnaires qui contiennent (au moins)
                les clefs du tableau ATTRIBUTS et la clef CLASSE

    Sortie: list - tableau des k dictionnaires contenu dans BDD
                   les plus "proches" de a_classer
    """
    pass


def classification(k, a_classer, BDD):
    """
    k - int, entier strictement positif (nombre de voisins)
    a_classer - dict, dictionnaires qui contient (au moins)
                      les clefs du tableau ATTRIBUTS
    BDD - list, Tableau de dictionnaires qui contiennent (au moins)
                les clefs du tableau ATTRIBUTS et la clef CLASSE

    Sortie: str - CLASSE de a_classer obtenue selon le principe k-NN
    """
    pass

Vous pouvez tester ensuite ces fonctions à l'aide des instructions ci-dessous.

Exemple de tests

>>> joueur1 = {'Nom': 'Quentin BÉTHUNE', 'Type poste': 'Avant', 'Taille (en cm)': 183, 'Poids (en kg)': 112}
>>> joueur2 = {'Nom': 'Fritz LEE', 'Type poste': '3ème ligne', 'Taille (en cm)': 188, 'Poids (en kg)': 107}
>>> distance(joueur1, joueur2)
10

>>> joueur_a_tester = {'Nom': 'Apisai NAQALEVU', 'Type poste': 'Trois-Quarts', 'Taille (en cm)': 188, 'Poids (en kg)': 104}
>>> k_plus_proches(1, joueur_a_tester, joueurs)
[{'Nom': 'Tom DARLET', 'Type poste': '3ème ligne', 'Taille (en cm)': 188, 'Poids (en kg)': 104}]

>>> k_plus_proches(5, joueur_a_tester, joueurs)
[{'Nom': 'Tom DARLET', 'Type poste': '3ème ligne', 'Taille (en cm)': 188, 'Poids (en kg)': 104},
 {'Nom': 'Kitione KAMIKAMICA', 'Type poste': '3ème ligne', 'Taille (en cm)': 188, 'Poids (en kg)': 105},
 {'Nom': 'Jaco VISAGIE', 'Type poste': 'Avant', 'Taille (en cm)': 188, 'Poids (en kg)': 105},
 {'Nom': 'Mahamadou DIABY', 'Type poste': '3ème ligne', 'Taille (en cm)': 188, 'Poids (en kg)': 105},
 {'Nom': 'Peniami Nasali NARISIA', 'Type poste': 'Avant', 'Taille (en cm)': 187, 'Poids (en kg)': 104}]

>>> for k in range(1, 11):
...     print(classification(k, joueur_a_tester, joueurs))
3ème ligne
3ème ligne
3ème ligne
3ème ligne
3ème ligne
3ème ligne
3ème ligne
3ème ligne
3ème ligne
3ème ligne
3ème ligne

Constatation

Le poste du joueur testé est 'Trois-Quarts'. Pourtant notre algorithme nous indique que ce joueur est 3ème ligne !

Partie B - Recherche de performance☘

Pour essayer de compenser la constatation précédente, nous pouvons tester deux pistes : modifier la définition de la distance et/ou rechercher la valeur de k qui renverra la « meilleure » prédiction pour un groupe de joueurs dont ont connaît déjà le type de poste.

  1. Modifiez la fonction distance() en prenant comme référence la distance euclidienne plutôt que la distance de Manhattan.

    Exemple de tests

    >>> for k in range(1, 11):
...     print(classification(k, joueur_a_tester, joueurs))
3ème ligne
3ème ligne
3ème ligne
3ème ligne
3ème ligne
3ème ligne
3ème ligne
3ème ligne
3ème ligne
3ème ligne
3ème ligne

    Bon, cette modification ne semble pas avoir d'effet...

  2. Enregistrez le fichier joueurs_TESTS.csv dans votre répertoire de travail, puis importez les données de ce fichier dans la variable joueurs_a_tester.

  3. Complétez la définition de la fonction comparaison() qui renvoie le nombre de joueurs de la table joueurs_a_tester pour lesquels le type de poste prédit par la fonction classification() n'est pas celui du joueur.
    Cette fonction doit utiliser au maximum les variables globales définies au début du programme.

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
    def comparaison(k, base_a_tester, BDD):
    """
    k - int, entier strictement positif
    base_a_tester - list, Tableau de dictionnaires qui contiennent (au moins)
                    les clefs du tableau ATTRIBUTS et la clef CLASSE
    BDD - list, Tableau de dictionnaires qui contiennent (au moins)
                les clefs du tableau ATTRIBUTS et la clef CLASSE

    Sortie: int - nombre de données de base_a_tester pour lesquelles la
            valeur de l'attribut CLASSE necorrespond pas à celle obtenue
            selon le principe k-NN
    """

  4. En testant les valeurs de k comprises entre 1 et 40, déterminez la valeur de k pour laquelle la prédiction est la plus fiable.
    Appelez l'enseignant pour lui donner la réponse.

  5. Peut-on obtenir mieux en revenant à la distance de Manhattan ?