Exercices d'entraînement☘

Ces exercices doivent être utilisés pour vous entraîner à programmer. Ils sont généralement accompagnés d'aide et de leur solution pour vous permettre de progresser.

Avant de vous précipiter sur ces solutions dès la première difficulté, n'oubliez pas les conseils suivants :

Avez-vous bien fait un schéma au brouillon pour visualiser le problème posé ?
Avez-vous essayé de rédiger un algorithme en français, avec vos propres mots, avant de vous lancer dans la programmation sur machine ?
Avez-vous utilisé des affichages intermédiaires, des print(), pour visualiser au fur et à mesure le contenu des variables ?
Avez-vous testé le programme avec les propositions de tests donnés dans l'exercice ?
Avez-vous testé le programme avec de nouveaux tests, différents de ceux proposés ?

Rappels

Chaque programme Python doit être sauvegardé sous forme de fichier texte avec l'extension .py.
Enregistrez ce fichier dans le dossier [G05_Algo_Gloutons] avec le nom donné à l'exercice : ProgG05.51.py, ProgG05.52.py, etc...
Pour exécuter ce programme, il suffit de le sauvegarder puis d'appuyer sur la touche [F5].

Le programme principal doit contenir un appel au module doctest :

##----- Programme principal et tests -----##
if __name__ == '__main__':
    import doctest
    doctest.testmod()

La plupart des exercices de cette page (et des suivantes) nécessiteront de réfléchir à une stratégie gloutonne (une règle de choix) avant de chercher à programmer qoui que ce soit...

ProgG05.51 - Parcourir une matrice☘

Raisonnement déjà travaillé dans ce TP, pour vérifier que vous avez bien compris le principe///

Le problème☘

Dans une grille de dimensions n × m, dont chaque case contient un nombre, on part de la cellule (0, 0) et on se rend dans la cellule (n-1, m-1). Les seuls déplacements autorisés sont les déplacements vers la droite et vers le bas. La contrainte est d'emprunter le chemin pour lequel la somme des nombres rencontrés est la plus petite.

Exemple☘

0	0	8	3	2	5
2	4	2	7	7	1
8	3	5	1	8	7
6	8	3	4	4	9
4	4	3	1	3	2

Le chemin optimal a pour somme 22 :

0	0	8	3	2	5
2	4	2	7	7	1
8	3	5	1	8	7
6	8	3	4	4	9
4	4	3	1	3	2

Questions☘

Déterminez une stratégie gloutonne pour parcourir ce tableau.

Une réponse
Une manière d'envisager la résolution du problème est de se dire :
« Depuis chaque case, je vais vers la voisine dont la valeur est la plus petite. »

Appliquez cette stratégie pour déterminez « à la main » (sur votre cahier) le chemin de somme minimale pour parcourir le tableau suivant :

4	2	7	4	2	7
4	8	8	1	4	7
4	1	4	6	8	4
8	1	2	5	2	6
1	1	9	1	3	7

Une réponse

On obtient un chemin de somme 46.

4	2	7	4	2	7
4	8	8	1	4	7
4	1	4	6	8	4
8	1	2	5	2	6
1	1	9	1	3	7

Cette stratégie semble-t-elle optimale ?

Une réponse

Il existe des chemins de somme inférieure. Le chemin optimal a pour somme 32.

4	2	7	4	2	7
4	8	8	1	4	7
4	1	4	6	8	4
8	1	2	5	2	6
1	1	9	1	3	7

Complétez la définition de la fonction parcours_mini() qui prend en paramètre une matrice tab de nombres et qui renvoie, sous la forme d'un tableau, la liste des coordonnées des cases à parcourir pour aller de tab[0][0] à
tab[n-1][m-1] en appliquant l'algorithme ci-dessus.

def parcours_mini(tab):
    """
    tab - list, Tableau de tableaux contenant des nombres
    Sortie: list - Tableau des couples de coordonnées à parcourir pour
            aller de la première à la dernière case du tableau tab
            en appliquant un principe glouton pour minimiser la somme
            totale des cases parcourues
    >>> tab = [[2, 2, 4, 4, 9, 0], [7, 0, 2, 2, 0, 2], [0, 5, 7, 3, 5, 2], [2, 6, 1, 0, 4, 7], [5, 2, 0, 6, 6, 9]]
    >>> parcours_mini(tab)
    [(0, 0), (0, 1), (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (2, 5), (3, 5), (4, 5)]
    """

Une piste

N'oubliez pas les bords !
Dans certains cas, ce ne sont plus deux choix de déplacement qui s'offrent à nous, mais un seul...

Une solution

def parcours_mini(tab):
    """
    tab - list, Tableau de tableaux contenant des nombres
    Sortie: list - Tableau des couples de coordonnées à parcourir pour
            aller de la première à la dernière case du tableau tab
            en appliquant un principe glouton pour minimiser la somme
            totale des cases parcourues
    >>> tab = [[2, 2, 4, 4, 9, 0], [7, 0, 2, 2, 0, 2], [0, 5, 7, 3, 5, 2], [2, 6, 1, 0, 4, 7], [5, 2, 0, 6, 6, 9]]
    >>> parcours_mini(tab)
    [(0, 0), (0, 1), (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (2, 5), (3, 5), (4, 5)]
    """
    n = len(tab)
    m = len(tab[0])
    i = 0
    j = 0
    result = [(i, j)]
    while i != n-1 or j != m-1:
        if i == n-1:
            j = j+1
        elif j == m-1:
            i = i+1
        elif tab [i+1][j] < tab[i][j+1]:
            i = i+1
        else:
            j = j+1
        result.append((i, j))
    return result

Testez cette fonction avec la matrice ci-dessous :

Matrice de test

tab = [[0, 0, 8, 3, 2, 5],
       [2, 4, 2, 7, 7, 1],
       [8, 3, 5, 1, 8, 7],
       [6, 8, 3, 4, 4, 9],
       [4, 4, 3, 1, 3, 2]]

Une solution

>>> tab = [[0, 0, 8, 3, 2, 5], 
          [2, 4, 2, 7, 7, 1],
          [8, 3, 5, 1, 8, 7],
          [6, 8, 3, 4, 4, 9],
          [4, 4, 3, 1, 3, 2]]
>>> parcours_mini(tab)
[(0, 0), (0, 1), (1, 1), (1, 2), (2, 2), (2, 3), (3, 3), (4, 3), (4, 4), (4, 5)]

Exercice G05.52☘

Cet exercice est à réaliser entièrement sur votre cahier

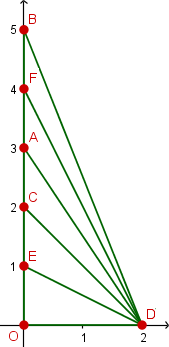itineraire Différentes villes (O, A, B, C, D, E et F) sont représentées dans un repère orthonormé.
Les villes sont reliées entre elles par des routes tracées en vert.

Un routier part de la ville O (origine du repère) et doit définir un itinéraire qui le fera passer par chacune des autres villes A, B, C, D, E, F (l'ordre de parcours n'est pas important). Son itinéraire s'arrête lorsqu'il a atteint la dernière ville à visiter.

Un choix glouton serait : « rejoindre à tout moment la ville la plus proche ». Ainsi, d'une ville-étape à la suivante, on minimise la longueur de la nouvelle étape.

En appliquant ce choix, déterminez l'ordre dans lequel ces villes sont parcourues.
Une réponse
- Entre O et E, la distance est 1 alors qu'entre O et D, la distance est 2.
  Le routier se rend en E.
- Entre E et C, la distance est 1 alors qu'entre E et D, la distance est $\sqrt{5}$ (théorème de Pythagore...).
  Le routier se rend en C.
- Entre C et A, la distance est 1 alors qu'entre C et D, la distance est $\sqrt{8}$ .
  Le routier se rend en A.
- Entre A et F, la distance est 1 alors qu'entre A et D, la distance est $\sqrt{13}$ .
  Le routier se rend en F.
- Entre F et B, la distance est 1 alors qu'entre F et D, la distance est $\sqrt{20}$ .
  Le routier se rend en B.
- Le routier se rend ensuite en D (seule ville non parcourue).
  Il aura parcouru les villes dans l'ordre O, E, C, A, F, B puis D...
Ce choix minimise-t-il la distance totale parcourue ? Justifiez.

Une réponse
Le parcours précédent donne comme distance totale $5+\sqrt{29}$ .
Il y a plus court en commençant d'abord par D :
O, D, E, C, A, F puis B.
La distance totale parcourue est alors $2+\sqrt{5}+4 = 6 + \sqrt{5}$ .