Division euclidienne

On rappelle dans cette page la notion de division euclidienne (ou division entière) d'un entier naturel $a$ par un entier naturel $b$.

Définition du quotient et du reste

Pour tout entier naturel $a$, et tout entier naturel $b$ non nul, il existe un unique couple d'entiers $(q ; r)$ tel que l'on ait $0 \leqslant r \leqslant b-1$ et $a = b \times q + r$.

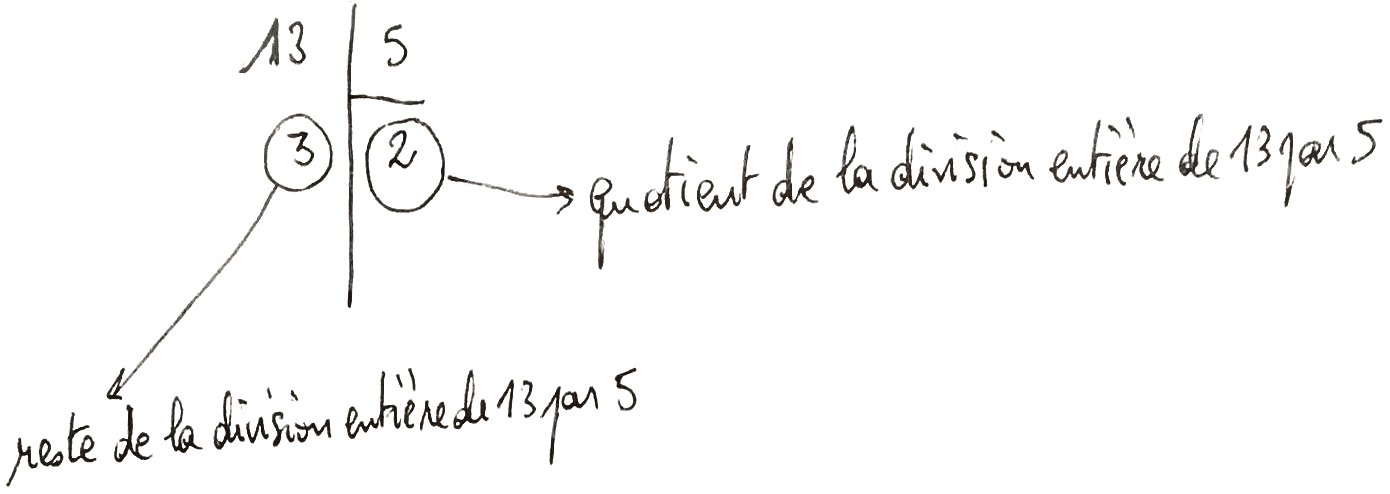
• L'entier $q$ est appelé quotient de la division entière de $a$ par $b$.
• L'entier $r$ est appelé reste de la division entière de $a$ par $b$.

Remarque (conséquence de l'unicité)

Soit $S$ un entier naturel.

Si l'on trouve, d'une façon ou d'une autre, un entier $q$ et un entier $r$ tel que $0\leqslant r \leqslant 9$ et $S = 10 q+r$ alors $r$ est nécessairement le reste de la division entière de $S$ par 10, $q$ est nécessairement le quotient de cette division.
Par exemple, $346 = 340+6 = 34 \times 10+6$.

Cela explique que le chiffre des unités d'un entier $n$ (en base 10) est nécessairement le reste de la division entière de $n$ par 10.

Définition de la partie entière

Tout réel $x$ non entier est compris strictement entre deux entiers consécutifs.
En d'autres termes, il existe un entier $n$ tel que $n < x < n+1$.

• L'entier $n$ est appelé sol de $x$ (ou partie entière de $x$), on le note en général $\lfloor x\rfloor$.
• L'entier $n+1$ est appelé plafond de $x$, on le note en général $\lceil x\rceil$.

Pour un entier n, on pose $\lfloor n \rfloor = \lceil n \rceil = n$ (l'entier est entre deux étages : à la fois sol et plafond).

En Python

Le sol (la partie entière) est obtenu par la fonction floor() du module math.
Le plafond est obtenu par la fonction ceil() du module math.

>>> import math
>>> math.floor(3.14)
3
>>> math.ceil(3.14)
4

Propriété

Soient $a$ et $b$ deux entiers naturels, avec $b$ non nul.

Le quotient de la division entière de $a$ par $b$ est le sol de $\frac{a}{b}$ : $q = \lfloor \frac{a}{b} \rfloor$.

• En d'autres termes, $q$ est le plus grand entier inférieur ou égal à $\frac{a}{b}$.

• En d'autres termes encore, $q$ est l'unique entier vérifiant $q \leqslant \frac{a}{b} < q+1$.

Exemple

Soit $S$ une somme à payer (en euros).
On souhaite donner un maximum de billets de 10€ pour payer cette somme $S$. Alors, le nombre de billets $q$ donnés vérifie $10q \leqslant S < 10(q+1)$ (avec $q$ billets, on a payé au plus la somme $S$ ; avec un billet de plus, on dépasserait $S$).
On a donc $q \leqslant \frac{S}{10} < q+1$ : $q$ est le quotient de la division de $S$ par 10.