Algorithmes usuels sur les images☘
Une image matricielle est donc représentée en machine comme un tableau à deux dimensions : la largeur et la hauteur. Parcourir l’ensemble des pixels de cette image nécessite donc d’utiliser une double boucle « Pour », c’est-à-dire deux boucles « Pour » imbriquées l’une dans l’autre.
L’illustration ci-contre permet de visualiser un parcours « classique »,
de gauche à droite et de haut en bas.
Pour chaque ordonnee dans la hauteur :
Pour chaque abscisse dans la largeur :
instructions qui tiennent compte de l’encodage couleur
Les algorithmes présentés dans cette partie sont des « grands classiques » du traitement d’image. Ces algorithmes nécessitent d’utiliser une image source.
Il est ensuite plus facile de les appliquer pour concevoir une nouvelle image à partir de cette image source plutôt que vouloir directement modifier cette image source.
D'une image en couleurs vers des nuances de gris☘
Pour chaque ordonnee dans la hauteur :
Pour chaque abscisse dans la largeur :
(r, g, b) ← couleur_du_pixel_parcouru
gris = (r+g+b)/3
couleur_pixel_nouvelle_image ← (gris, gris, gris)
Passage au négatif☘
Cet algorithme dépend de l’encodage couleur de l’image source.
On considère de plus que les intensités sont codées sur un octet (entiers de
0 à 255).
| Couleur d'un pixel de l'image source | Couleur d'un pixel de l'image « négatif » | |
|---|---|---|
| encodage « noir & blanc » | c |
1-c |
| encodage « nuances de gris » (sur 1 octet) | g |
255-g |
| encodage « RGB » (sur 3 octets) | (r, g, b) |
(255–r, 255–g, 255–b) |
| encodage « RGBs » (sur 4 octets) | (r, g, b, a) |
(255–r, 255–g, 255–b, 255–a) |
Symétries☘
On considère un pixel quelconque de l’image source. Les coordonnées de ce pixel sont notées (x, y).
-
Dans le cas d'une symétrie horizontale, les coordonnées du pixel symétrique sont
(x, hauteur-1-y):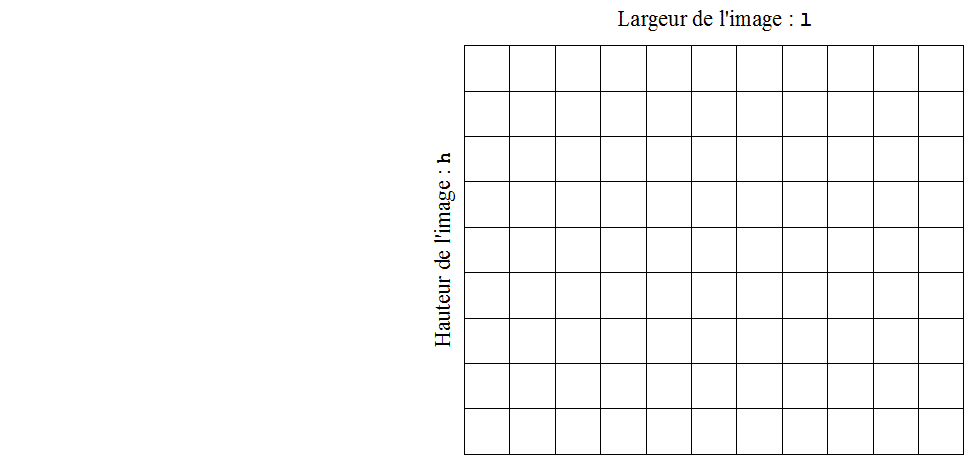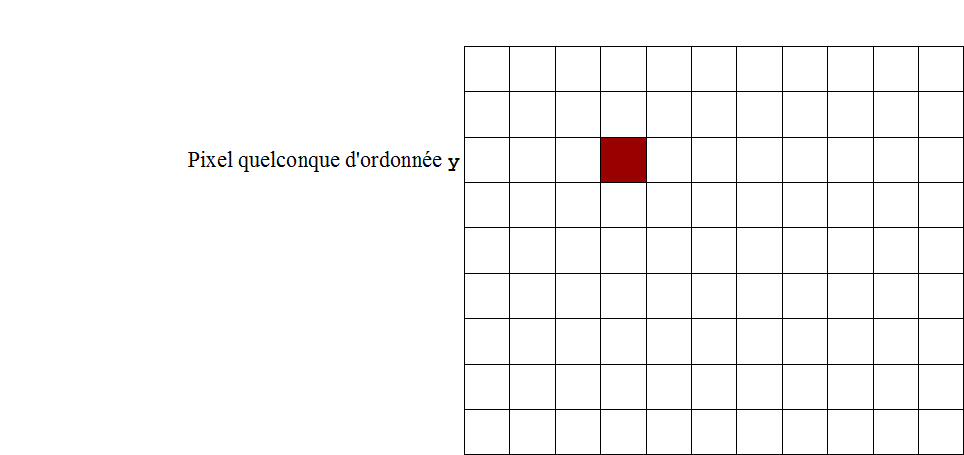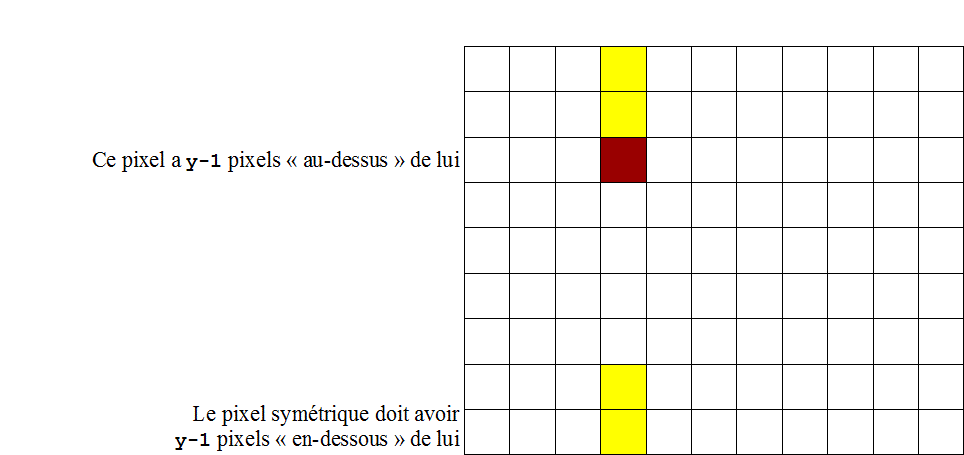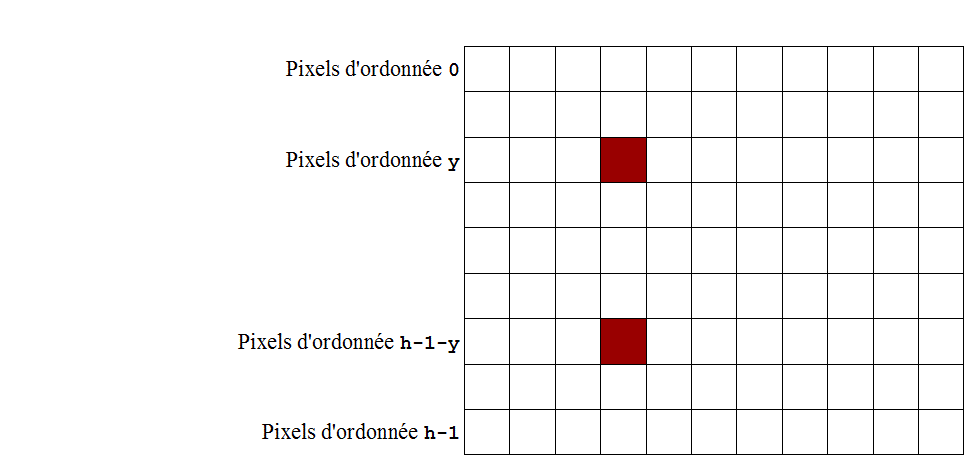
-
Dans le cas d'une symétrie verticale, les coordonnées du pixel symétrique sont
(largeur-1-x, y):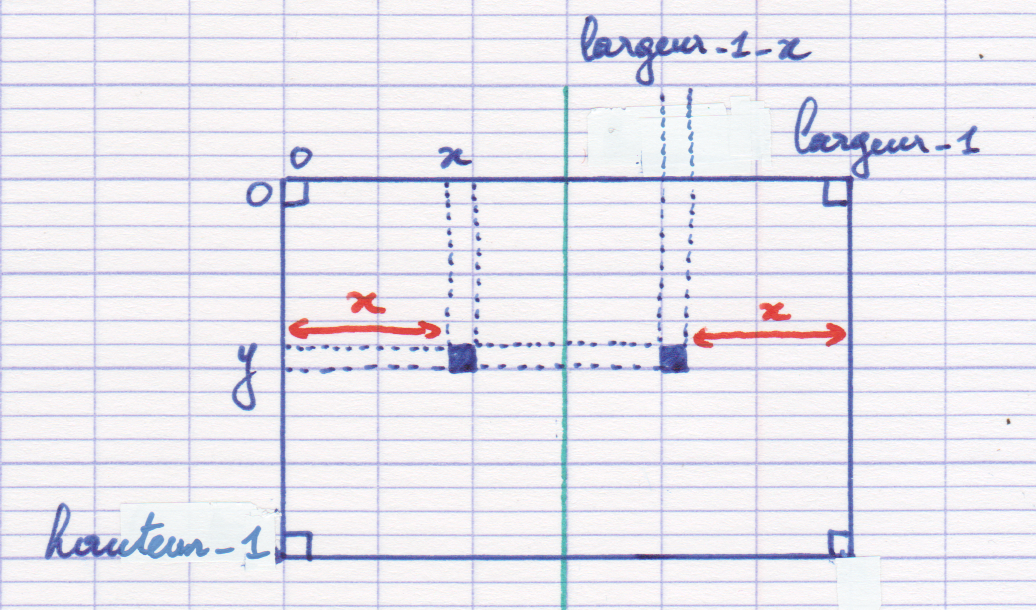
Rotation de 90° dans le sens inverse des aiguilles d'une montre☘
L'image n'est pas modifiée, elle est simplement tournée. Ce ne sont donc pas les composantes couleur sur lesquelles il faut intervenir mais les coordonnées de chaque pixel.
Pour trouver les opérations mathématiques à effectuer, le plus simple est de
faire un schéma de l'image dans lequel on place un pixel quelconque de
coordonnées (x, y) avant la rotation, puis le même pixel après la rotation.
En déterminant ses nouvelles coordonnées à partir du pixel haut-gauche de
l'image tournée, on peut en déduire les calculs à effectuer sur les
coordonnées (x, y) d'origine.
On en déduit l'illustration ci-dessous. Les figures de couleurs représentent
les pixels des 4 coins de l'image, avec leurs coordonnées, avant, puis après
la rotation. Le pixel quelconque de coordonnées (x, y) est représenté par le
losange rouge «évidé».
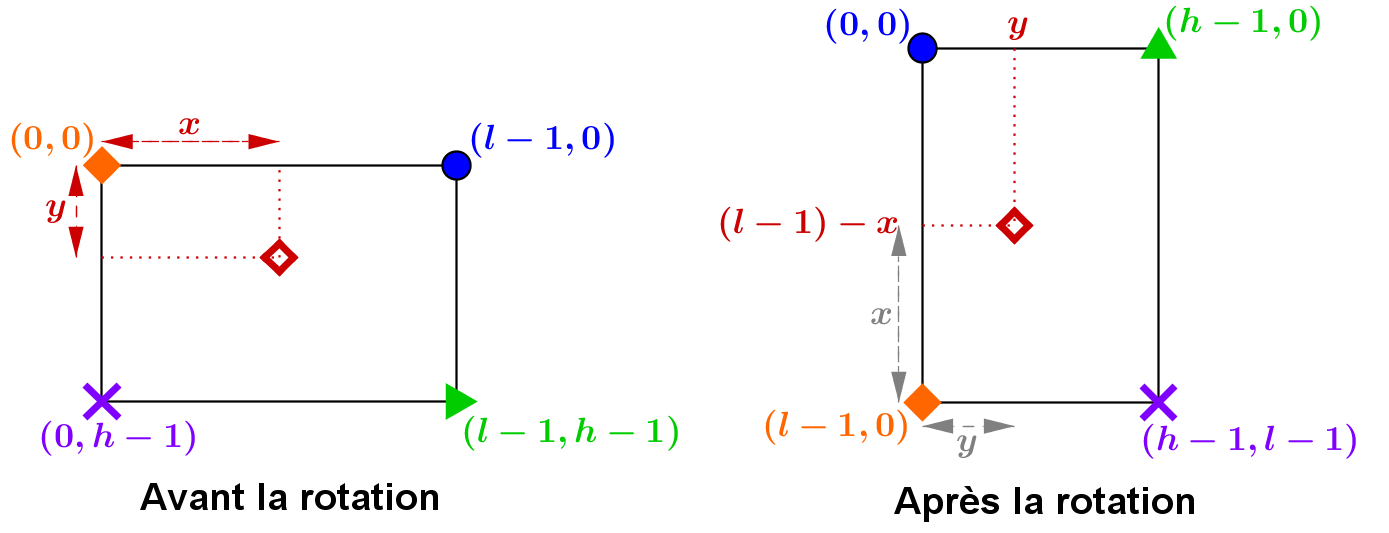
Dans l’image résultat après rotation de 90° dans le sens direct, les
coordonnées du pixel correspondant sont (y, largeur-1-x).