Des iris

Dans le dossier [NSI], créez le dossier [G06_Algo_KNN].

Téléchargez le fichier à compléter TPG06.10.py (clic droit -> [Enregistrer sous]) et enregistrez-le dans le dossier [G06_Algo_KNN].

Consignes communes à chaque partie

Le programme principal contient un appel au module doctest :

##----- Programme principal et tests -----##
if __name__ == '__main__':
    import doctest
    doctest.testmod()

Chacune des fonctions devra passer les tests proposés.
Il faudra aussi ajouter vos propres tests dans le « main » afin de vous entraîner à en réaliser.

Préambule - La base iris

La petite base de données Iris est un ensemble de résultats (datant du début du vingtième siècle) très souvent utilisée dans les cours d'initiation à l'intelligence artificielle ou aux statistiques.

Nous allons l'utiliser à partir d'un fichier csv.

1. Téléchargez et sauvegardez ce fichier dans votre répertoire de travail.

2. Vérifiez (à l'aide d'un éditeur de texte comme Notepad++ par exemple) que les premières lignes de ce fichier sont :

   longueur du sépale	largeur du sépale	espèce
   6.0	3.4	Iris-versicolor
   6.2	2.2	Iris-versicolor
   5.0	3.0	Iris-setosa
   7.2	3.2	Iris-virginica
   5.6	2.5	Iris-versicolor
   5.1	3.3	Iris-setosa
   6.0	2.9	Iris-versicolor

   En colonne 1 on trouve une mesure de la longueur du sépale, en colonne 2 une mesure de sa largeur. Enfin en colonne 3, le type d'iris. Il y a trois types (ce sera nos « classes ») : setosa, versicolor et virginica.

   Iris setosa	Iris versicolor	Iris virginica

3. En utilisant la bibliothèque fonctions_csv.py déjà utilisée dans le traitement des données, complétez le programme principal, le main, pour :

   1. importer la base Iris sous la forme d'une table de dictionnaires (nommez cette table iris).
   2. convertir les attributs nécessaire en flottants.
   3. afficher chaque dictionnaire de cette table pour vérifier votre importation.
   Affichage à obtenir

   Voici les premières lignes de la table contenue dans la variable iris :

   {'longueur du sépale': 6.0, 'largeur du sépale': 3.4, 'espèce': 'Iris-versicolor'}
   {'longueur du sépale': 6.2, 'largeur du sépale': 2.2, 'espèce': 'Iris-versicolor'}
   {'longueur du sépale': 5.0, 'largeur du sépale': 3.0, 'espèce': 'Iris-setosa'}
   {'longueur du sépale': 7.2, 'largeur du sépale': 3.2, 'espèce': 'Iris-virginica'}
   {'longueur du sépale': 5.6, 'largeur du sépale': 2.5, 'espèce': 'Iris-versicolor'}
   {'longueur du sépale': 5.1, 'largeur du sépale': 3.3, 'espèce': 'Iris-setosa'}
   {'longueur du sépale': 6.0, 'largeur du sépale': 2.9, 'espèce': 'Iris-versicolor'}
   

4. La fonction representation() a été définie dans le programme pour visualiser ces données à l'aide de la bibliothèque matplotlib.pyplot comme dans la page Représentation Graphique.
   Appliquez cette fonction à la variable iris et vérifiez que vous obtenez la représentation graphique suivante :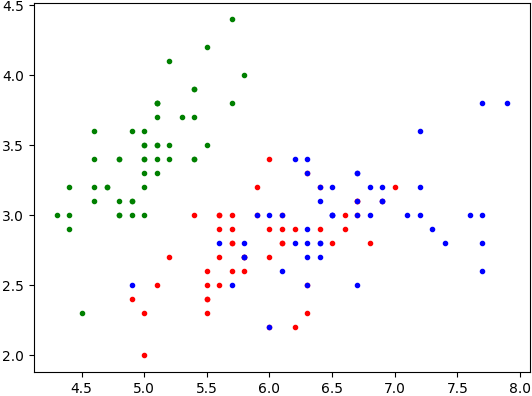

Partie A - En route vers l'algorithme $k$-NN

Lorsqu'on a une nouvelle fleur à classifier, la représentation graphique précédente montre que les mesures choisies ne permettent pas une conclusion immédiate puisque la frontière entre les rouges et les bleus est floue.

On décide d'appliquer le principe de l'algorithme $k$-NN pour pouvoir classer une nouvelle fleur parmi les trois espèces.

A noter

Le botaniste sait bien évidemment les distinguer.
Nous souhaitons en fait réaliser une classification automatique : c'est la base des algorithmes d'IA (plus spécifiquement du « machine learning »).

Ce type de classification automatique est la base par exemple de la capacité de votre téléphone à regrouper de façon automatique toutes les photos concernant une même personne.

1. Complétez la définition de la fonction distance() qui prend en paramètres deux iris (c'est à dire deux dictionnaires de la table iris) et qui renvoie la « distance euclidienne » entre eux (un iris est identifié au point de coordonnées (longueur du sépale, largeur du sépale) comme dans la représentation graphique précédente).

   def distance(fleur1, fleur2):
       """
       fleur1, fleurs2 - dict, dictionnaires dont les clefs sont :
                         'longueur du sépale', 'largeur du sépale' et 'espèce'
       Sortie: float - Distance euclidienne entre deux fleurs
       >>> fleur1 = {'longueur du sépale': 6.7, 'largeur du sépale': 3.0, 'espèce': 'Iris-virginica'}
       >>> fleur2 = {'longueur du sépale': 5.1, 'largeur du sépale': 2.5, 'espèce': 'Iris-versicolor'}
       >>> distance(fleur1, fleur2)
       1.6763054614240216
       >>> distance(fleur1, fleur1)
       0.0
       """
   

2. Complétez la définition de la fonction plus_proche_voisin() qui prend en paramètres un iris a_classer (c'est-à-dire un dictionnaire représentant un iris, mais sans la clef espèce) et un tableau de dictionnaires (c'est-à-dire la table iris). Cette fonction renvoie le dictionnaire du tableau le plus proche de la fleur a_classer passée en paramètre.

   def plus_proche_voisin(a_classer, fleurs):
       """
       a_classer - dict, dictionnaires dont les clefs sont :
                   'longueur du sépale' et 'largeur du sépale'
       fleurs - list, Tableau de dictionnaires dont les clefs sont :
               'longueur du sépale', l'abscisse du point
               'largeur du sépale', l'ordonnée du point
               'espèce', classe/couleur ('Iris-setosa', 'Iris-versicolor' ou 'Iris-virginica')
   
       Sortie: dict - dictionnaire contenu dans fleurs et le plus "proche" de a_classer
       >>> a_classer = {'longueur du sépale': 5.9, 'largeur du sépale': 2.8}
       >>> plus_proche_voisin(a_classer, iris)
       {'longueur du sépale': 5.8, 'largeur du sépale': 2.8, 'espèce': 'Iris-virginica'}
       """
   

3. Vérifiez le travail réalisé en appliquant la fonction represente_plus_proche() à la fleur {'longueur du sépale': 5.9, 'largeur du sépale': 2.8} et à la table iris. Vous devez obtenir le résultat ci-dessous :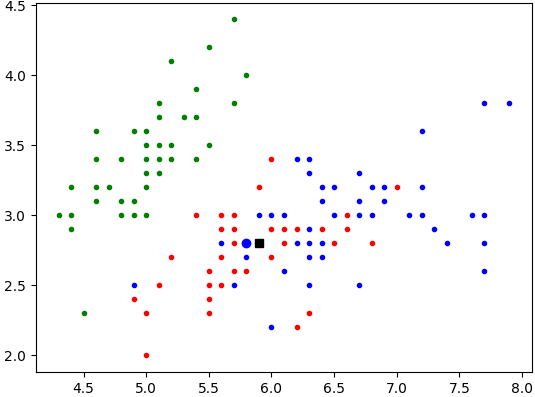

Partie B - Les $k$ plus proches voisins

1. Complétez la définition de la fonction k_plus_proches() en utilisant le principe suivant :

   • Pour chacune des fleurs de la base, ajouter la clef distance associée à la distance entre cette fleur et la fleur a_classer.
   • Trier la base par ordre croissant de distance (rappelez-vous la méthode étudiée dans le chapitre traitement des données).
   • Supprimez la clef 'distance' pour chaque fleur.
   • Renvoyer les $k$ premières fleurs.

   def k_plus_proches(k, a_classer, fleurs):
       """
       k - int, entier strictement positif (nombre de voisins)
       a_classer - dict, dictionnaires dont les clefs sont :
                   'longueur du sépale' et 'largeur du sépale'
       fleurs - list, Tableau de dictionnaires dont les clefs sont :
               'longueur du sépale', l'abscisse du point
               'largeur du sépale', l'ordonnée du point
               'espèce', classe/couleur ('Iris-setosa', 'Iris-versicolor' ou 'Iris-virginica')
   
       Sortie: list - tableau des k dictionnaires contenu dans fleurs
                      les plus "proches" de a_classer
       >>> a_classer = {'longueur du sépale': 5.9, 'largeur du sépale': 2.8}
       >>> k_plus_proches(3, a_classer, iris)
       [{'longueur du sépale': 5.8, 'largeur du sépale': 2.8, 'espèce': 'Iris-virginica'}, {'longueur du sépale': 6.0, 'largeur du sépale': 2.7, 'espèce': 'Iris-versicolor'}, {'longueur du sépale': 6.0, 'largeur du sépale': 2.9, 'espèce': 'Iris-versicolor'}]
       """
   

2. Vérifiez le travail réalisé en appliquant la fonction represente_k_plus_proche() à la fleur {'longueur du sépale': 5.9, 'largeur du sépale': 2.8} et à la table iris.

   1. Pour $k=3$, vous devez obtenir le résultat ci-dessous :

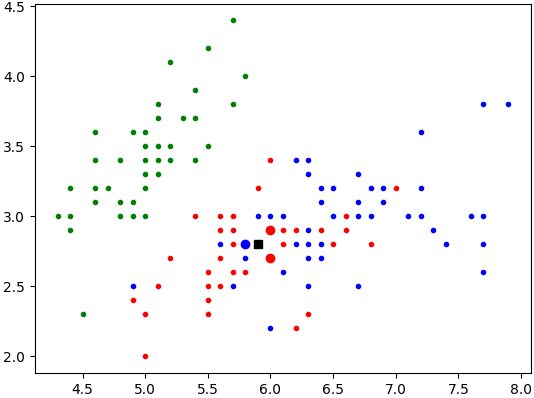
   2. Pour $k=7$, vous devez obtenir le résultat ci-dessous :

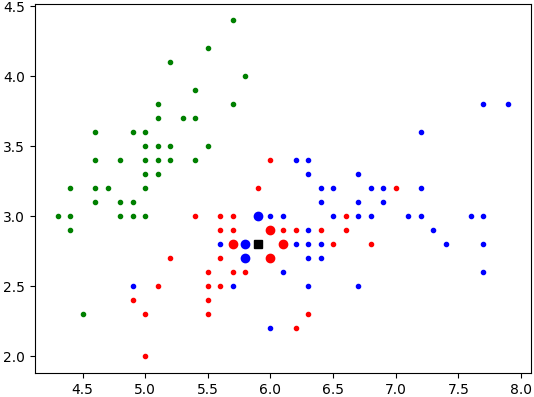
Dans les deux cas, les fleurs issues de notre base de données iris.csv qui sont majoritaires parmi les plus proches (au sens défini ci-dessus) de notre iris de longueur de sépale 5.9 et de largeur de sépale 2.8 sont des versicolor.

Avec le critère $3$-NN et le critère $7$-NN, on décide donc que cette nouvelle fleur est, elle aussi, une versicolor.

Remarque

Soulignons une fois de plus que le principe utilisé ici est très simple par rapport aux algorithmes modernes utilisés en IA. Les résultats ne seront sans doute pas bons par rapport à ce que peut obtenir un téléphone récent (il existe des applications de reconnaissance des plantes sur vos smartphones, testez-en une à votre prochaine sortie !)

Partie C - Classification automatique

1. Complétez la définition de la fonction classification() qui prend en paramètres un entier k, une fleur a_classer et une table de dictionnaires fleurs.
   Cette fonction renvoie la classe que l'on octroie à cette fleur a_classer donnée par le principe $k$-NN.

   def classification(k, a_classer, fleurs):
       """
       k - int, entier strictement positif (nombre de voisins)
       a_classer - dict, dictionnaires dont les clefs sont :
                   'longueur du sépale' et 'largeur du sépale'
       fleurs - list, Tableau de dictionnaires dont les clefs sont :
               'longueur du sépale', l'abscisse du point
               'largeur du sépale', l'ordonnée du point
               'espèce', classe/couleur ('Iris-setosa', 'Iris-versicolor' ou 'Iris-virginica')
   
       Sortie: str - classe (espèce) de a_classer obtenue selon le principe k-NN
       >>> a_classer = {'longueur du sépale': 5.9, 'largeur du sépale': 2.8}
       >>> classification(3, a_classer, iris)
       'Iris-versicolor'
       """
   

   Une piste

   On peut créer un dictionnaire vide qui se remplit au fur et à mesure.
   Les clefs seront les valeurs de l'attribut 'espèce' de chaque fleur associées au nombre de fois où cet attribut est rencontré dans la table des $k$ plus proches voisins.

2. Testez cette fonction à l'aide des exemples suivants.
   Que peut-on en conclure ?

   Exemples de tests

   >>> fleur = {'longueur du sépale': 6, 'largeur du sépale': 2.8}
   >>> classification(1, fleur, iris)
   
   >>> classification(3, fleur, iris)
   
   >>> classification(7, fleur, iris)
   
   >>> classification(9, fleur, iris)
   

   Une réponse

   >>> fleur = {'longueur du sépale': 6, 'largeur du sépale': 2.8}
   >>> classification(1, fleur, iris)
   'Iris-versicolor'
   
   >>> classification(3, fleur, iris)
   'Iris-versicolor'
   
   >>> classification(7, fleur, iris)
   'Iris-versicolor'
   
   >>> classification(9, fleur, iris)
   'Iris-virginica'
   

   Cet exemple permet de voir qu'avec $k$ = 9, la conclusion est différente d'avec lesvaleurs de $k$ inférieures à 9.

   On pourrait alors croire que le procédé semble peu fiable. C'est pourquoi on complète en général l'implémentation de l'algorithme par des tests de fiabilité à l'aide de données sur lesquelles on connaît la réponse.

   Pour une plus grande fiabilité, la taille de la base de données et le choix de $k$ sont deux facteurs importants.

Partie D - Pour aller plus loin

En fait, la base de données iris est un peu plus complète et comporte également des données sur la largeur et la longueur des pétales.

A noter

Si la taille de la base de données et le choix de $k$ sont deux facteurs importants pour la fiabilité de prédiction, le nombre et le choix des attributs qui vont alimenter la base jouent évidemment également un rôle crucial.

1. Téléchargez le fichier complet puis enregistrez-le dans votre répertoire de travail.

2. Modifiez une seule fonction de votre programme pour tenir compte de ces mesures (attributs) supplémentaires.

   Exemples de tests

   >>> fleur = {'longueur du sépale': 6, 'largeur du sépale': 2.8, 'longueur du pétale': 5.0, 'largeur du pétale': 2.3}
   >>> classification(1, fleur, iris_complet)
   'Iris-virginica'
   
   >>> classification(3, fleur, iris_complet)
   'Iris-virginica'
   
   >>> classification(7, fleur, iris_complet)
   'Iris-virginica'
   
   >>> classification(9, fleur, iris_complet)
   'Iris-virginica'
   

   Une piste

   Il s'agit essentiellement de modifier la fonction distance() qui doit maintenant tenir compte du fait que l'on a quatre données quantitatives par fleur.

   On calculera la distance avec la même formule mais avec quatre termes sous la racine (c'est la distance euclidienne entre deux points dans un espace de dimension 4). Ainsi, cette distance entre $A(x, y, z, t)$ et $B(a, b, c, d)$ est : $\sqrt{(x-a)^2 + (y-b)^2 + (z-c)^2 + (t-d)^2}$.